scVI:https://docs.scvi-tools.org/en/stable/user_guide/models/scvi.html
MultiVI:https://docs.scvi-tools.org/en/stable/user_guide/models/multivi.html
目录
- scVI
- 生成
- 推理
- 任务
- MultiVI
- 生成
- 推理
scVI
single cell variational inference提出了一个灵活的scRNA-seq数据生成模型。scVI功能全面,可以扩展到大规模数据集(处理超过1万个细胞),局限性在于:1.需要GPU才能快速推理,2.与线性方法不同,潜在空间不可解释。
生成
scVI将包含细胞和基因的scRNA-seq基因表达矩阵 X X X作为输入( N N N个细胞, G G G个基因),此外,一个设计的矩阵 S S S包含 p p p个观测协变量,比如day,donor等等,这是可选的输入。虽然 S S S可以包含离散协变量和连续协变量,但在下文中,我们假设它仅包含一个具有 K K K个类别的离散协变量,这代表了具有多批次数据的常见情况。
对于细胞 n n n和基因 g g g,scVI用下面过程生成观测的UMI计数 x n g x_{ng} xng(其中, s n s_{n} sn为细胞 n n n的batch id): z n ∼ N o r m a l ( 0 , I ) l n ∼ l o g N o r m a l ( l μ ⊤ s n , l σ 2 ⊤ s n ) ρ n = f w ( z n , s n ) π n g = f h g ( z n , s n ) x n g ∼ O b s e r v a t i o n M o d e l ( l n ρ n , θ g , π n g ) z_{n}\sim Normal(0,I)\\ l_{n}\sim logNormal(l_{\mu}^{\top}s_{n},l_{\sigma^{2}}^{\top}s_{n})\\ \rho_{n}=f_{w}(z_{n},s_{n})\\ \pi_{ng}=f_{h}^{g}(z_{n},s_{n})\\ x_{ng}\sim ObservationModel(l_{n}\rho_{n},\theta_{g},\pi_{ng}) zn∼Normal(0,I)ln∼logNormal(lμ⊤sn,lσ2⊤sn)ρn=fw(zn,sn)πng=fhg(zn,sn)xng∼ObservationModel(lnρn,θg,πng)简而言之,每个基因的基因表达取决于细胞特异性的潜在变量 z n z_{n} zn。先验参数 l μ l_{\mu} lμ 和 l σ 2 l_{\sigma^{2}} lσ2 是根据所有细胞的对数大小在不同批次之间计算得出的均值和方差。表达数据是从一个基于计数的似然分布生成的,这里称为 O b s e r v a t i o n M o d e l ObservationModel ObservationModel,默认为ZINB分布,也可以是更简单的NB分布。
生成过程使用两个神经网络: f w ( z n , s n ) : R d × { 0 , 1 } K → Δ G − 1 f h ( z n , s n ) : R d × { 0 , 1 } K → ( 0 , 1 ) ⊤ f_{w}(z_{n},s_{n}):\mathbb{R}^{d}\times\left\{0,1\right\}^{K}\rightarrow\Delta^{G-1}\\f_{h}(z_{n},s_{n}):\mathbb{R}^{d}\times\left\{0,1\right\}^{K}\rightarrow(0,1)^{\top} fw(zn,sn):Rd×{0,1}K→ΔG−1fh(zn,sn):Rd×{0,1}K→(0,1)⊤分别解码去噪基因表达和ZINB概率。
下表为潜在变量以及描述:
| 潜在变量 | 描述 |
|---|---|
| z n ∈ R d z_{n}\in\mathbb{R}^{d} zn∈Rd | 细胞状态的低维表示 |
| ρ n ∈ Δ G − 1 \rho_{n}\in\Delta^{G-1} ρn∈ΔG−1 | 去噪的基因表达。这是一个cell内总和为1的向量 |
| l n ∈ ( 0 , ∞ ) l_{n}\in(0,∞) ln∈(0,∞) | RNA 文库大小。 这里它被建模为一个潜在变量,但 scVI 最近的默认设置是将文库大小视为观察到的,等于当前细胞 n n n的总 RNA UMI 计数 |
| θ g ∈ ( 0 , ∞ ) \theta_{g}\in(0,∞) θg∈(0,∞) | NB的Inverse dispersion。例如,可以通过在模型初始化期间传递dispersion=“gene-batch”来将其设置为特定于基因或批次 |
推理
scVI 使用变分推理来学习模型参数(神经网络参数、Inverse dispersion等)和具有以下分解的近似后验分布: q η ( z n , l n ∣ x n ) = q η ( z n ∣ x n , s n ) q η ( l n ∣ x n ) q_{\eta}(z_{n},l_{n}|x_{n})=q_{\eta}(z_{n}|x_{n},s_{n})q_{\eta}(l_{n}|x_{n}) qη(zn,ln∣xn)=qη(zn∣xn,sn)qη(ln∣xn)这里 η \eta η是对应于推理神经网络(编码器)的一组参数。值得注意的是,默认情况下,scVI 仅接收表达数据作为输入(没有观测到的细胞水平协变量)。根据经验,通过让编码器将这些item的串联 q η ( z n , l n ∣ x n , s n ) q_{\eta}(z_{n},l_{n}|x_{n},s_{n}) qη(zn,ln∣xn,sn) 作为输入,我们并没有看到太大的差异。
任务
下面是scVI可以执行的任务。
降维:近似的后验 q η ( z n ∣ x n , s n ) q_{\eta}(z_{n}|x_{n},s_{n}) qη(zn∣xn,sn)被返回获得低维表示。
transfer :scVI可以根据参考数据进行训练,然后将细胞水平协变量(比如细胞类型注释)转移到查询数据。
基因表达的插补:scVI返回近似后验下 ρ n \rho_{n} ρn的期望值。对于细胞 n n n,可以写成: E q η ( z n ∣ x n ) [ f w ( z n , s n ) ] \mathbb{E}_{q_{\eta}(z_{n}|x_{n})}[f_{w}(z_{n},s_{n})] Eqη(zn∣xn)[fw(zn,sn)]
差异分析:scVI在估计后的插补数据上执行差异分析。
生成模拟数据:可以从 z n z_{n} zn进行采样,重新模拟生成新的细胞数据。
MultiVI
multiVI是一个多模态生成模型,能够整合多组学的scRNA-seq和scATAC-seq数据,训练后,可用于许多常见的下游任务,也可用于缺失模态的插补。
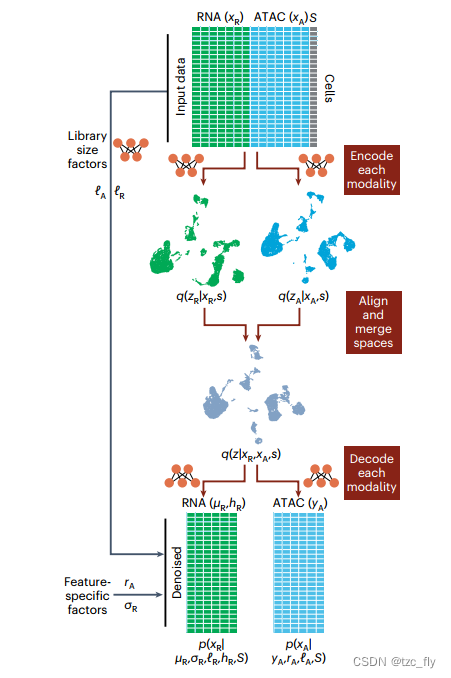
- 图1:其中输入数据由ATAC、RNA两种数据类型组成(或者加上蛋白质模态)。变量 S S S表示实验协变量,如批次或实验条件( S S S是可选的输入)。每个数据模态被编码成模态无关的潜在表示,然后,这些表示被合并到一个联合潜在空间。
生成
MultiVI的输入为多模态单细胞矩阵 X m u l t X_{mult} Xmult,包含 N N N个细胞, G G G个基因,以及 M M M个基因区域(peaks),或者仅 X r n a X_{rna} Xrna( N N N个细胞和 G G G个基因),或者仅 X a t a c X_{atac} Xatac( N N N个细胞和 M M M个peaks,peaks可能是二值化的或者整数计数)。此外,一个设计的矩阵 S S S包含 p p p个观测协变量,比如day等,这是可选的输入。虽然 S S S可以包含离散协变量和连续协变量,但在下文中,我们假设它仅包含一个具有 K K K个类别的离散协变量,这代表了具有多批次数据的常见情况。
对于细胞 n n n和基因 g g g以及peaks j j j,MultiVI用下面过程生成观测的UMI计数 x n g x_{ng} xng和 y n j y_{nj} ynj: z n ∼ N o r m a l ( 0 , I ) l n ∼ l o g N o r m a l ( l μ ⊤ s n , l σ 2 ⊤ s n ) ρ n = f w ( z n , s n ) π n g = f h g ( z n , s n ) x n g ∼ O b s e r v a t i o n M o d e l ( l n ρ n , θ g , π n g ) p n j = g z j ( z n , s n ) l n = f l ( y n ) y n j ∼ B e r n o u l l i ( p n j ⋅ l n ⋅ r j ) z_{n}\sim Normal(0,I)\\ l_{n}\sim logNormal(l_{\mu}^{\top}s_{n},l_{\sigma^{2}}^{\top}s_{n})\\ \rho_{n}=f_{w}(z_{n},s_{n})\\ \pi_{ng}=f_{h}^{g}(z_{n},s_{n})\\ x_{ng}\sim ObservationModel(l_{n}\rho_{n},\theta_{g},\pi_{ng})\\ p_{nj}=g_{z}^{j}(z_{n},s_{n})\\ l_{n}=f_{l}(y_{n})\\ y_{nj}\sim Bernoulli(p_{nj}\cdot l_{n}\cdot r_{j}) zn∼Normal(0,I)ln∼logNormal(lμ⊤sn,lσ2⊤sn)ρn=fw(zn,sn)πng=fhg(zn,sn)xng∼ObservationModel(lnρn,θg,πng)pnj=gzj(zn,sn)ln=fl(yn)ynj∼Bernoulli(pnj⋅ln⋅rj)对于scRNA-seq,先验参数 l μ l_{\mu} lμ 和 l σ 2 l_{\sigma^{2}} lσ2 是根据所有细胞的对数大小在不同批次之间计算得出的均值和方差。表达数据是从一个基于计数的似然分布生成的,这里称为 O b s e r v a t i o n M o d e l ObservationModel ObservationModel,默认为ZINB分布,也可以是更简单的NB分布。
对于scATAC-seq,检测可访问区域( y n j > 0 y_{nj}>0 ynj>0)是由伯努利随机变量生成的,该变量取决于细胞特异性潜在变量 z n z_{n} zn,该变量捕获生物异质性。另外有两个辅助的缩放因子 l n l_{n} ln和 r j r_{j} rj,分别考虑了特定于细胞和特定于region的批次效应。
MultiVI 的生成过程使用神经网络: f w ( z n , s n ) : R d × { 0 , 1 } K → Δ G − 1 f h ( z n , s n ) : R d × { 0 , 1 } K → ( 0 , 1 ) ⊤ g z ( z n , s n ) : R d × { 0 , 1 } K → [ 0 , 1 ] M f_{w}(z_{n},s_{n}):\mathbb{R}^{d}\times\left\{0,1\right\}^{K}\rightarrow\Delta^{G-1}\\f_{h}(z_{n},s_{n}):\mathbb{R}^{d}\times\left\{0,1\right\}^{K}\rightarrow(0,1)^{\top}\\ g_{z}(z_{n},s_{n}):\mathbb{R}^{d}\times\left\{0,1\right\}^{K}\rightarrow[0,1]^{M} fw(zn,sn):Rd×{0,1}K→ΔG−1fh(zn,sn):Rd×{0,1}K→(0,1)⊤gz(zn,sn):Rd×{0,1}K→[0,1]M分别解码去噪基因表达、非零膨胀概率(仅当使用 ZINB 时)并估计可访问区域的概率。
推理
MultiVI 使用变分推理来学习模型参数,并得到具有以下分解的近似后验分布: q η ( z n , l n ∣ x n ) = q η ( z n ∣ x n , y n , s n ) q η ( l n ∣ x n ) q_{\eta}(z_{n},l_{n}|x_{n})=q_{\eta}(z_{n}|x_{n},y_{n},s_{n})q_{\eta}(l_{n}|x_{n}) qη(zn,ln∣xn)=qη(zn∣xn,yn,sn)qη(ln∣xn)其中, z n z_{n} zn被确定性地计算为变分近似 z n r n a z_{n}^{rna} znrna和 z n a t a c z_{n}^{atac} znatac的两个潜在变量的平均值。这两个变量是正态的,因此 z n z_{n} zn是正态的。
当获得隐变量后,使用生成模型即可完成不同模态的数据还原。
MultiVI的局限:因为 z n z_{n} zn需要获得两个模态的 z n r n a z_{n}^{rna} znrna和 z n a t a c z_{n}^{atac} znatac均值,MultiVI在非联合测量数据上的整合能力有限。




)







,ceil,floor,abs,比较两者或多者为较大值或较小值,round,找数组和对象的随机数)





)
