前言
通常说的Tarjan算法指的是计算机科学家Robert Tarjan提出的多个与图连通性有关的算法,通常包括:
- 强连通性
- 有向图的强连通分量(SCC)缩点
- 无向图的边双连通性
- 割边
- 无向图的边双连通(e-DCC)分量缩点
- 无向图的点双连通性
- 割点
- 无向图的点双连通分量(v-DCC)缩点(圆方树)
有向图的双连通性与支配树有关。
对树进行dfs,会有如下过程:
- 进:进入节点 u u u
- 主循环
- 离:离开节点 u u u
vector<int>a[N+5];临接链表存图对树进行dfs:
void dfs(int u,int fa){进入节点ufor(auto&v:a[u]){主循环}离开节点u
}
Tarjan算法的执行步骤可以分为在这三部之内进行一些操作。
强连通性
定义
搜索树
对图进行dfs,每个节点只访问一次,访问到的节点和边构成dfs树(搜索树)。
从 1 1 1开始dfs,图中黑色的边就构成一个搜索树:

dfs的起点就是搜索树的根。
事实上由于从起点不一定能够到达图中所有点,如果我们对于未被访问的点继续dfs,可能会形成若干颗搜索树(dfs顺序:绿,红,蓝):

有向边的分类
把图中的一条有向边按照其起点终点在搜索树上的关系分为五类:
- 树边 \color{black}树边 树边:dfs树上的边
- 非树边:
- 后向边 ( 返祖边 ) \color{red}后向边(返祖边) 后向边(返祖边):由dfs树上的节点指向其祖先的边
- 前向边 \color{blue}前向边 前向边:由dfs树上的节点指向其子孙的边
- 横叉边 \color{green}横叉边 横叉边:同一颗dfs树上某一颗子树上的节点指向另一颗子树的边
- 其他边:由图中一颗dfs树指向图中另一颗dfs树的边
性质
树上一个连通块内深度最浅的点是唯一的,否则假如说 x ≠ y x\not =y x=y属于连通块,且 d e p x = d e p y dep_x=dep_y depx=depy,并且是连通块内深度最浅的点,则 l c a x , y lca_{x,y} lcax,y属于连通块,并且 d e p l c a x , y dep_{lca_{x,y}} deplcax,y更浅,矛盾。
一个连通分量中深度最浅的点称为连通分量的根。
时间戳
对树进行dfs,同时把访问到的节点的编号加入序列,就得到dfs序列,简称dfs序,节点 u u u的dfs序中的位置称为 u u u的时间戳,记作 d f n u dfn_u dfnu。
dfs序就是多叉树的先根遍历序列。
有向图的强连通分量(SCC)缩点
流程
Tarjan算法求强连通分量(SCC)的过程,最终求出一个数组,叫做 { s c c n } \{scc_n\} {sccn},其中 s c c u scc_u sccu表示点 u u u所在的强连通分量的根的编号。
Tarjan算法的过程在dfs中进行,dfs(u)的过程是:
- 访问到以前未被访问的节点 u u u
- 计算 d f n u , l o w u dfn_u,low_u dfnu,lowu
- 把 u u u入栈
- 枚举 u u u的后继 v v v
- 若 v v v未被访问:
递归进 v v v:dfs(v)
更新 l o w u low_u lowu:low[u]=min(low[u],low[v]) - 若 v v v已被访问,但是仍在栈中:
更新 l o w u low_u lowu:low[u]=min(low[u],dfn[v])
- 若 v v v未被访问:
- 若此时 d f n u = l o w u dfn_u=low_u dfnu=lowu:
则说明栈中从栈顶到 u u u点构成强连通分量,且 u u u是强连通分量的根
把这些点全都弹出,并且更新 s c c scc scc数组
然后我们对每个未被访问的点进行dfs,就计算出了全图的SCC情况。
写成代码就是:
int dfn[N+5],cnt,low[N+5];
stack<int>s;
bool vis[N+5];
vector<int> a[N+5];
int scc[N+5];int dfs1(int u) {if(dfn[u]) return dfn[u];dfn[u]=low[u]=++cnt;s.push(u);vis[u]=1;维护元素u是否在栈中for(auto&v:a[u])if(!dfn[v]||vis[v])更新条件:未被访问 or 仍在栈中low[u]=min(low[u],dfs1(v));if(low[u]==dfn[u]) {如果满足条件就说明栈中从u到栈顶的元素都与u强连通while(s.top()^u)scc[s.top()]=u,vis[s.top()]=0,s.pop();scc[s.top()]=u,vis[s.top()]=0,s.pop();}return low[u];
}
int main(){int n,m;cin>>n>>m;for(int u,v,i=1;i<=m;i++){cin>>u>>v;a[u].push_back(v);}for(int i=1;i<=n;i++)dfs1(i);对每个未被访问的位置都做一遍Tarjan,如果i已经被访问,那么进入dfs后会立即返回。
}
Tarjan算法求SCC的要点主要有三个:
- 额外维护一个栈
- l o w u low_u lowu更新条件:未被访问/仍在栈中
- SCC判定条件:当 l o w u = d f n u low_u=dfn_u lowu=dfnu时,目前在栈顶到 u u u之间的节点与 u u u强连通。
显然Tarjan算法的时间复杂度为 O ( n + m ) O(n+m) O(n+m)
证明
接下来证明这个算法的正确性。
追溯值
容易发现,此时 l o w u low_u lowu的含义是,假设刚刚进入 u u u时,从 u u u开始至多走一条非树边后终止,能够访问到的仍在栈中的点(栈维持在 u u u刚刚入栈后的状态不变),的最小时间戳。
Tarjan算法在求SCC,割边,割点,e-DCC,v-DCC中追溯值的定义略有不同。
本文无意严格证明追溯值的意义,因为这可能需要一些数学刻画,会让事情变得麻烦。
你可以认为,我们是知道了追溯值的定义之后,通过对应的代码了维护这个定义,这一点可以通过归纳证明。
我们某一时刻称 x x x在 y y y前,或称 y y y在 x x x后,当且仅当此时 x , y x,y x,y都在栈中,并且此时 y y y在栈中的位置在 x x x到栈顶的位置之间。(包括 x x x和栈顶)
我们考虑dfs中,最后一次返回节点 u u u之后,若 l o w u = d f n u low_u=dfn_u lowu=dfnu的时刻:(可以认为是刚进入if(low[u]==dfn[u])语句,啥也没干的时刻)
定理1
对于 x x x在 u u u后, x x x是 u u u的子孙。即 u u u是 x x x的祖先。
在 u u u和栈顶之间的元素都是进入节点 u u u之后进栈的,因此它们都在 u u u的子树内。
定理2
若 x x x是 y y y的祖先,则 l o w x ≤ l o w y low_x\leq low_y lowx≤lowy
定理3
节点 x x x在栈内是 x x x与 u u u强连通的必要条件
只需证明其逆否命题:若 x x x不在栈内,则 x , u x,u x,u不强连通。
- 若 x x x未进栈:
显然从 u u u不可达 x x x,证完。 - 若 x x x已经出栈:
说明 d f n x < d f n u dfn_x<dfn_u dfnx<dfnu- 若从 x x x可达 u u u:
由于 d f n x < d f n u dfn_x<dfn_u dfnx<dfnu, x x x在dfs树上必然是 u u u的祖先,显然祖先必不可能先于子孙出栈,矛盾。 - 若从 x x x不可达 u u u:
证完。
- 若从 x x x可达 u u u:
QED.
定理4
x x x在 u u u后,是 x , u x,u x,u强连通的必要条件。
只需证明其逆否命题:若 x x x在 u u u前,则 x , u x,u x,u不强连通
为了证明 x , u x,u x,u不强连通,我们断言 u u u不可达 x x x,否则 u u u可达 x x x。
首先可知 d f n x < d f n u dfn_x<dfn_u dfnx<dfnu,则 x x x不是 u u u的子孙,
则必然存在一条由 u u u到 x x x的路径,并且这条路径的某一步肯定从 u u u的子树内走到子树外,即路径上存在一条边 ( u ′ , v ′ ) (u',v') (u′,v′),使得 u ′ u' u′是 u u u的子孙,而 v ′ v' v′不是。否则,一直在 u u u的子树内行走,不可能走到 x x x。
- 若访问到 u ′ u' u′时, v ′ v' v′仍在栈中:
则 l o w u ′ low_{u'} lowu′必然被 l o w v ′ low_{v'} lowv′更新,说明: l o w u ′ ≤ l o w v ′ low_{u'}\leq low_{v'} lowu′≤lowv′
因为 v ′ v' v′不在 u u u子树内,并且dfs的过程进行到即将离开 u u u时,因此所有不在 u u u子树内的点的时间戳都被 d f n u dfn_u dfnu要小,即: d f n v ′ < d f n u dfn_{v'}<dfn_u dfnv′<dfnu
此时注意到 l o w u ≤ l o w u ′ ≤ l o w v ′ ≤ d f n v ′ < d f n u low_u\leq low_{u'}\leq low_{v'}\leq dfn_{v'}<dfn_u lowu≤lowu′≤lowv′≤dfnv′<dfnu,即 l o w u < d f n u low_u<dfn_u lowu<dfnu,但我们知道 l o w u = d f n u low_u=dfn_u lowu=dfnu,矛盾。 - 若访问到 u ′ u' u′时, v ′ v' v′已不在栈中:
若 u , x u,x u,x强连通,则 x x x可达 u u u,则 u , u ′ , v ′ , x u,u',v',x u,u′,v′,x强连通,注意到 v ′ v' v′此时不在栈内,与定理3冲突,矛盾。
QED.
定理5
若 x x x在 u u u后:
d f n x > l o w x ≥ d f n u ( x ≠ u ) dfn_x>low_x\geq dfn_u(x\not=u) dfnx>lowx≥dfnu(x=u)
首先证明 d f n x > l o w x dfn_x>low_x dfnx>lowx,这是因为首先有 d f n x ≥ l o w x dfn_x\geq low_x dfnx≥lowx
并且 d f n x ≠ l o w x dfn_x\not=low_x dfnx=lowx,否则 x x x不在栈中。
接下来证明 l o w x ≥ d f n u low_x\geq dfn_u lowx≥dfnu:
因为定理1、2, l o w x ≥ l o w u = d f n u low_x\geq low_u=dfn_u lowx≥lowu=dfnu
定理6
x x x在 u u u后,是 x , u x,u x,u强连通的充分条件。
假设栈中目前,从 u u u到栈顶的元素依次是: { x 0 = u , x 1 , x 2 , . . . , x k = x , . . . } \{x_0=u,x_1,x_2,...,x_k=x,...\} {x0=u,x1,x2,...,xk=x,...}
归纳假设 x i < k x_{i<k} xi<k与 u u u强连通,要证明 u , x u,x u,x强连通。
由于 u u u显然可达 x x x,所以只需证明, x x x可达 u u u。
根据定理5,我们知道 d f n u ≤ l o w x < d f n x dfn_u\leq low_x<dfn_x dfnu≤lowx<dfnx,因此设 l o w x = d f n y low_x=dfn_y lowx=dfny。
- 若 y y y仍在栈中:
则 d f n y = l o w x ≥ d f n u dfn_y=low_x\geq dfn_u dfny=lowx≥dfnu,则 y y y在 u u u后,且 y y y在 x x x前,则存在 0 ≤ i < k 0\leq i<k 0≤i<k满足 x i = y x_i=y xi=y,则说明 x x x可达 y y y,又因为 y y y可达 u u u,因此 x x x可达 u u u,证毕。 - 若 y y y不在栈中:
因为更新 l o w x low_x lowx得到了 d f n y dfn_y dfny,说明dfs进入节点 x x x时 y y y仍在栈中,或是 y = x y=x y=x。
但若 y = x y=x y=x,这说明 d f n x = l o w x dfn_x=low_x dfnx=lowx,违反定理5,矛盾。
因此,dfs进入节点 x x x时 y y y仍在栈中,但是dfs最后一次回到节点 u u u时 y y y不在栈中,说明 y y y在搜索 u u u的子树的过程中被弹出了。
假设 y y y是在dfs即将离开 s s s时被弹出。显然有 d f n s ≤ d f n y = l o w x < d f n x dfn_s\leq dfn_y=low_x<dfn_x dfns≤dfny=lowx<dfnx,因此 s s s在 x x x之前进栈。
当访问到节点 x x x时, y y y在 x x x前,且 y y y仍在栈中,等到之后的某一时刻(这一时刻在最后一次返回到节点 u u u之前), y y y不在栈中,说明 y y y被弹出了,那么 y y y之后的所有元素,包括 x x x也应该被弹出了,则 x x x应该不在栈中,矛盾。
证毕。
定理7
根据定理4和定理6可知,最后一次返回节点 u u u之后, l o w u = d f n u low_u=dfn_u lowu=dfnu时 x x x在 u u u后,是 x x x与 u u u强连通的充要条件。
因此Tarjan算法求SCC是可行的。
实现
#include<iostream>
#include<vector>
#include<stack>
#include<algorithm>
using namespace std;
const int N=1e4;
int dfn[N+5],cnt,low[N+5];
stack<int>s;
bool vis[N+5];
vector<int> a[N+5];
int scc[N+5];
int dfs1(int u) {if(dfn[u]) return dfn[u];dfn[u]=low[u]=++cnt;s.push(u);vis[u]=1;for(auto&v:a[u])if(!dfn[v]||vis[v])low[u]=min(low[u],dfs1(v));if(low[u]==dfn[u]) {while(s.top()^u)scc[s.top()]=u,vis[s.top()]=0,s.pop();scc[s.top()]=u,vis[s.top()]=0,s.pop();}return low[u];
}
int h[N+5],f[N+5];
vector<int> b[N+5];
int dfs2(int u){if(vis[u]) return f[u];vis[u]=1;for(auto&v:b[u])f[u]=max(f[u],dfs2(v));return f[u]+=h[u];
}
int main(){int n,m;cin>>n>>m;for(int i=1;i<=n;i++) cin>>h[i];for(int u,v,i=1;i<=m;i++){cin>>u>>v;a[u].push_back(v);}for(int i=1;i<=n;i++)dfs1(i);for(int i=1;i<=n;i++)if(scc[i]^i)h[scc[i]]+=h[i];for(int u=1;u<=n;u++)for(auto&v:a[u])if(scc[v]^scc[u])b[scc[u]].push_back(scc[v]);for(int i=1;i<=n;i++)scc[i]==i&&dfs2(i);cout<<*max_element(f+1,f+1+n);
}
无向图的边双连通性
割边
若两个节点 x , y x,y x,y之间存在两条路径,使得这两条路径不经过相同的边,则称 x , y x,y x,y边双连通。
边双连通具有传递性,即 x , y x,y x,y边双连通, y , z y,z y,z边双连通,则 x , y x,y x,y边双连通。
如果一张无向图中,任意两个节点 x , y x,y x,y之间都存在两条路径,使得这两条路径不经过相同的边,则这张图称为边双连通图。
无向图中的极大边双连通子图称为边双连通分量。
在无向图中,如果删去一条无向边 ( u , v ) (u,v) (u,v)之后,存在两个节点原本可以互相到达,但是删去之后无法互相到达,则称这条边为割边。
注意割边是一个无向边。
割边也被称为“bridge”,即“桥”。或者叫做必进边。
容易发现边双连通分量的点集是互不相交的,即无向图 G G G的点集 V V V被划分为若干个边双连通分量。
显然,一张无向图内不存在割边是其边双连通的充要条件。
因此无向图的一个不存在割边的连通子图是边双连通分量,当且仅当其是极大的。
因此我们规定不允许走割边,形成若干连通块,每个连通块都是一个边双连通分量。
流程
Tarjan算法求割边的过程,最终求出一个bool数组,叫做 { c u t m } \{cut_m\} {cutm},其中 c u t i cut_i cuti表示边 i i i是否为割边。
dfs(u)表示目前dfs到了节点 u u u,其过程为:
-
访问到以前未被访问的节点 u u u
-
计算 d f n u , l o w u dfn_u,low_u dfnu,lowu
-
枚举 u u u的后继 v v v
- 若 v v v未被访问:
递归进 v v v:dfs(v)
更新 l o w u low_u lowu:low[u]=min(low[u],low[v])
如果 d f n u < l o w v dfn_u<low_v dfnu<lowv,那么从 u u u走到 v v v的这条边是割边。 - 若 v v v已被访问,但是从 u u u走到 v v v的无向边不是dfs到 u u u的边:
更新 l o w u low_u lowu:low[u]=min(low[u],dfn[v])
- 若 v v v未被访问:
-
返回
我们需要对每个未被访问的点dfs,换句话说需要对无向图的每个连通块都进行一遍Tarjan算法求割边的过程,这样就求出了整张图的割边情况。
写成代码就是:
int h[N+5],to[M*2+5],nxt[M*2+5],tot=1;
由于要判断正反边,因此用链式前向星存边
初始把tot设置为1的话,第一条边的编号就从2开始
这样的话,正边编号^反边编号=1,方便判断bool cut[M*2+5];
void add(int u,int v){nxt[++tot]=h[u];to[h[u]=tot]=v;
}
int dfn[N+5],cnt,low[N+5];int dfs(int u,int pre){if(dfn[u]) return dfn[u];dfn[u]=low[u]=++cnt;for(int i=h[u],v; (v=to[i]); i=nxt[i])if(!dfn[v]) {low[u]=min(low[u],dfs(v,i));cut[i]=dfn[u]<low[v];}else if(i^pre^1)low[u]=min(low[u],dfs(v,i));return low[u];
}
int main(){int n,m;cin>>n>>m;for(int u,v,i=1; i<=m; i++)cin>>u>>v,add(u,v),add(v,u);for(int i=1;i<=n;i++) dfs(i,0);0^1=1,一开始访问i,没有边不能走,因此pre=0
}
Tarjan算法求割边的要点主要有两个:
- l o w u low_u lowu更新条件:未被访问/没走反边
- 割边判断条件: v v v第一次被访问, d f n u < l o w v dfn_u<low_v dfnu<lowv,则这条边是割边
证明
接下来证明这个算法求割边的正确性。
考虑一个刚刚结束dfs(v),返回到dfs(u)的主循环的时刻,可以认为是在刚好要if(dfn[u]<low[v])之前。
记 f a x fa_x fax表示节点 x x x在搜索树上的父亲。我们知道有 f a v = u fa_v=u fav=u
追溯值
容易发现,此时 l o w u low_u lowu的含义是,假设刚刚进入 u u u时,从 u u u开始至多走一条非树边(并且不走 f a u fa_u fau到达 u u u的那条边)后终止,能够访问到的点的最小时间戳。这可以通过归纳证明。
定理1
若 x x x是 y y y的祖先,则 l o w x ≤ l o w y low_x\leq low_y lowx≤lowy
定理2
对于点 x x x有 f a = f a x fa=fa_x fa=fax, x x x子树内存在一条路径,不经过 f a fa fa访问到 x x x的边,就能到达 x x x子树外,是 f a fa fa访问到 x x x的边不是割边的充要条件。
证明:
必要性显然。
充分性(其实都挺显然):
因为从 x x x子树内走到了子树外,因此路径上必然存在一条边 ( u ′ , v ′ ) (u',v') (u′,v′),这条边不是 f a fa fa访问到 u u u的边,使得 u ′ u' u′在 x x x子树内, v ′ v' v′在 x x x子树外,否则路径上所有点都在 x x x子树内,矛盾。
假如说割掉从 f a fa fa访问到 x x x的边,由于存在边 ( u ′ , v ′ ) (u',v') (u′,v′),因此子树内与子树外仍然是连通的,因此 f a fa fa访问到 x x x的边不是割边,证毕。
定理3
d f n u < l o w v dfn_u<low_v dfnu<lowv是 u u u访问到 v v v的无向边是割边的充要条件。
(这其实暗含了非树边一定不是桥,因为无向非树边一定在至少一个回路上,而回路上的边一定不是桥。)
根据定义 d f n u < l o w v dfn_u<low_v dfnu<lowv,是 v v v内存在一条路径,不经过 u u u访问到 v v v的边,能够访问到 v v v子树外的点的充要条件,则根据定理2证毕。
因此Tarjan算法求割边的正确性是有保证的。
实现
#include<iostream>
#include<set>
#include<map>
using namespace std;
const int N=150,E=5000;
int h[N+5],to[2*E+5],nxt[2*E+5],tot=1;
void add(int u,int v){nxt[++tot]=h[u];to[h[u]=tot]=v;
}
bool cut[2*E+5];
int dfn[N+5],cnt,low[N+5];
int dfs(int u,int pre){if(dfn[u]) return dfn[u];dfn[u]=low[u]=++cnt;for(int i=h[u],v;(v=to[i]);i=nxt[i])if(!dfn[v]){low[u]=min(low[u],dfs(v,i));cut[i]=dfn[u]<low[v];}else if(i^1^pre)low[u]=min(low[u],dfs(v,i));return low[u];
}
int main(){int n,m;cin>>n>>m;for(int u,v,i=1;i<=m;i++)cin>>u>>v,add(u,v),add(v,u);for(int i=1;i<=n;i++)dfs(i,0);set<pair<int,int>> s;for(int u=1;u<=n;u++)for(int i=h[u],v;(v=to[i]);i=nxt[i])if(cut[i])s.insert({min(u,v),max(u,v)});for(auto&i:s)cout<<i.first<<' '<<i.second<<endl;
}
无向图的边双连通(e-DCC)分量缩点
这里求解边双连通分量采用两遍dfs法:
- 第一遍dfs跑Tarjan算法求出割边
- 第二遍dfs不允许走割边,对连通块进行染色
当然求割边也可以一遍dfs,但是这样就会修改Tarjan算法求割边的dfs代码,因为大家都不想背两份板子,所以我们不采用一遍dfs求割边的方法。
把边双连通分量缩成一个点,剩下的图一定是一棵树/森林,树边是原来的割边。
这是很显然的,因为如果缩边双之后存在一个环,那么环上对应的所有原图中的点,构成一个更大的边双连通分量。
实现
#include<iostream>
#include<vector>
using namespace std;
const int N=5e5,E=2e6;
int h[N+5],to[2*E+5],nxt[2*E+5],tot=1;
void add(int u,int v){nxt[++tot]=h[u];to[h[u]=tot]=v;
}
bool cut[2*E+5];
int dfn[N+5],low[N+5],cnt;
int dfs1(int u,int pre){if(dfn[u])return dfn[u];dfn[u]=low[u]=++cnt;for(int i=h[u],v;(v=to[i]);i=nxt[i])if(!dfn[v]){low[u]=min(low[u],dfs1(v,i));cut[i]=dfn[u]<low[v];}else if(i^pre^1)low[u]=min(low[u],dfs1(v,i));return low[u];
}
vector<int>ans;
bool vis[N+5];
void dfs2(int u){vis[u]=1;ans.push_back(u);for(int i=h[u],v;(v=to[i]);i=nxt[i])if(!cut[i]&&!vis[v])dfs2(v);
}
int main(){int n,m;cin>>n>>m;for(int i=1,u,v;i<=m;i++)cin>>u>>v,add(u,v),add(v,u);for(int i=1;i<=n;i++) dfs1(i,0);for(int u=1;u<=n;u++)for(int i=h[u];i;i=nxt[i])if(cut[i])cut[i^1]=1;int cnt=0;for(int i=1;i<=n;i++) if(!vis[i]) cnt++,dfs2(i);cout<<cnt<<endl;for(auto&i:vis) i=0;for(int i=1;i<=n;i++)if(!vis[i]){ans.resize(0);dfs2(i);cout<<ans.size()<<' ';for(auto&j:ans)cout<<j<<' ';cout<<endl;}
}
无向图的点双连通性
割点
如果两个节点 x , y x,y x,y之间存在两条路径,使得两条路径不经过相同的点(除了起点和终点),则称 x , y x,y x,y点双连通。
点双连通不具有传递性,例如 A , B A,B A,B点双连通, B , C B,C B,C点双连通,但是 A , C A,C A,C不点双连通:
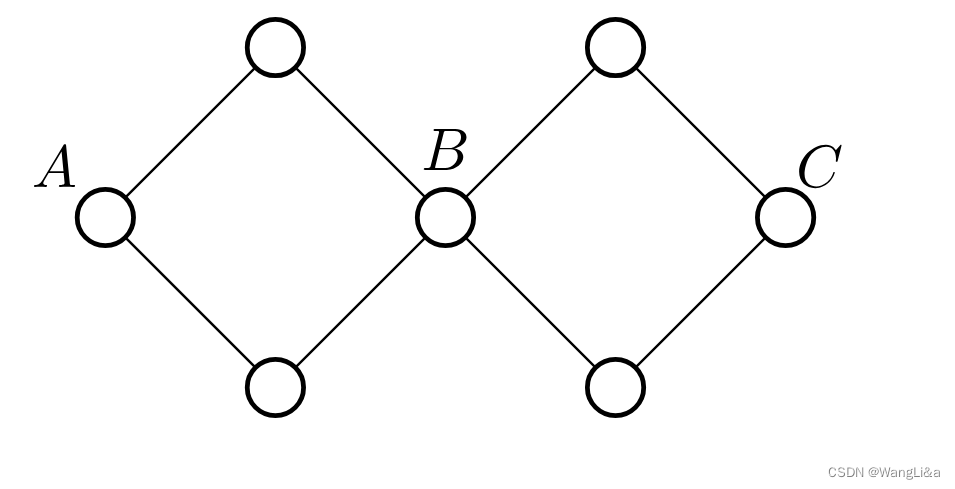
如果一张无向图中,任意两个节点 x , y x,y x,y之间都存在两条路径,使得这两条路径不经过相同的点(除了起点和终点),则这张图称为点双连通图。
无向图中的极大点双连通子图称为点双连通分量。
在无向图中,如果删去点 u u u(以及其所有连边)之后,存在两个节点原本可以互相到达,但是删去之后无法互相到达,则称这个点为割点。
割点又叫做割顶。或者叫做必经点。
或者说,删去点 u u u后使得连通块数量增加,则点 u u u称为无向图的割点。
因此孤立点不是割点,但是点双连通分量。只有两个点和连接这两个点的一条边组成的图是点双连通图,这个图中没有割点。
容易发现点双连通分量的点集有可能是相交的,但是其只可能在原图的割点处相交。
流程
Tarjan算法求割点的过程,最终求出一个bool数组,叫做 { c u t n } \{cut_n\} {cutn},其中 c u t i cut_i cuti表示点 i i i是否为割点。
dfs(u)表示目前dfs到了节点 u u u,其过程为:
-
访问到以前未被访问的节点 u u u
-
计算 d f n u , l o w u dfn_u,low_u dfnu,lowu
-
枚举 u u u的后继 v v v
- 若 v v v未被访问:
递归进 v v v:dfs(v)
更新 l o w u low_u lowu:low[u]=min(low[u],low[v])
如果 u u u不是dfs树的根, d f n u ≤ l o w v dfn_u\leq low_v dfnu≤lowv,那么 u u u是割点。
如果 u u u是dfs树的根,那么 u u u有两个及以上儿子时, u u u是割点。 - 若 v v v已被访问:
更新 l o w u low_u lowu:low[u]=min(low[u],dfn[v])
- 若 v v v未被访问:
-
返回
我们需要对每个未被访问的点dfs,换句话说需要对无向图的每个连通块都进行一遍Tarjan算法求割点的过程,这样就求出了整张图的割点情况。
写成代码就是:
vector<int>a[N+5];
int dfn[N+5],low[N+5],cnt;
bool cut[N+5];
int dfs(int u,bool k){if(dfn[u]) return dfn[u];dfn[u]=low[u]=++cnt;for(auto&v:a[u])if(!dfn[v]){low[u]=min(low[u],dfs(v,1));割点判定条件:u不为根时:dfn_u<=low_vu为根时:u至少有两个儿子,可以认为是u至少有两个dfn_u<=low_v的儿子因为u作为根节点,时间戳一定最早因此判定的时候可以把这两个综合起来:if(dfn[u]<=low[v])cut[u]=k,k=1; }else low[u]=min(low[u],dfs(v,1));return low[u];
}
int main(){int n,m;cin>>n>>m;for(int i=1,u,v;i<=m;i++)cin>>u>>v,a[u].push_back(v),a[v].push_back(u);for(int i=1;i<=n;i++) dfs(i,0);
}
Tarjan算法求割点的要点主要有两个:
- l o w u low_u lowu更新条件:未被访问
- 割点判定条件:
u u u不为根: d f n u ≤ l o w v dfn_u\leq low_v dfnu≤lowv
u u u为根: u u u至少有两个儿子 v v v(因为 u u u为根,因此它的儿子一定满足 d f n u ≤ l o w v dfn_u\leq low_v dfnu≤lowv)
证明
接下来证明Tarjan算法求割点的正确性。
追溯值
容易发现这里追溯值的定义是:从 u u u开始,至多走一条非树边后停止(并且回到父亲立即停止),能够访问到的节点对应的最小时间戳。
定理1
当 u u u为根节点时,它在dfs树上至少有两个儿子是 u u u是割点的充要条件。
证明:
当 u u u没有儿子( u u u为孤立点)或者 u u u只有一个儿子时,显然 u u u不是割点,因此具有必要性。
当 u u u有至少两个儿子时,由于dfs的过程,我们知道这两个儿子间一定不存在不经过点 u u u的路径,否则在递归进入第一个儿子时,就可以dfs到第二个儿子,这样就把 u u u的第二个儿子标记了, u u u就无法再次dfs进入 u u u的第二个儿子,矛盾。
因此 u u u符合割点的定义,具有充分性。
定理2
当 u u u不为根节点时,存在一个儿子 v v v满足 d f n u ≤ l o w v dfn_u\leq low_v dfnu≤lowv是 u u u为割点的充要条件。
根据追溯值的定义显然。
图示,注意尽管我们把返祖边画成了有向边,但是其事实上是无向边:
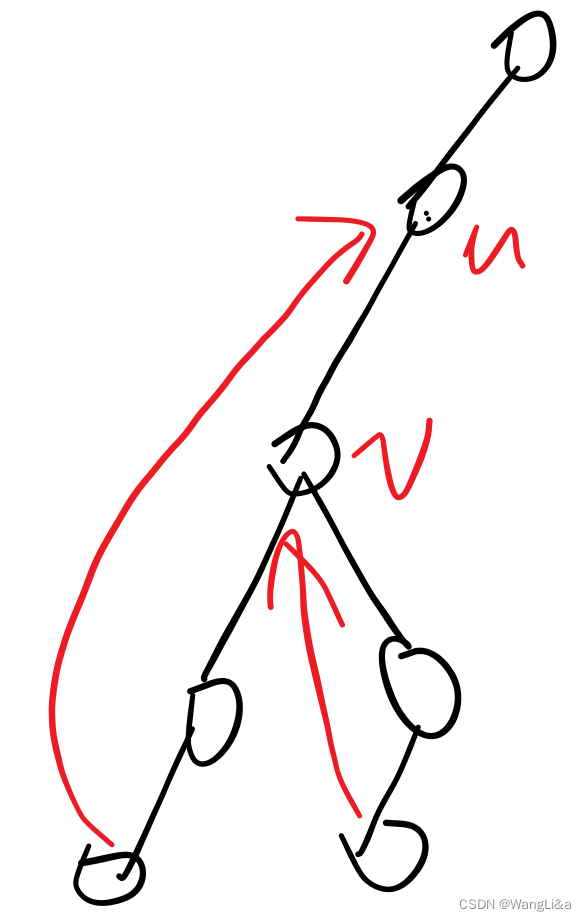
于是我们就证明了Tarjan算法求割点的正确性。
实现
#include<iostream>
#include<vector>
#include<numeric>
using namespace std;
const int N=2e4;
vector<int>a[N+5];
int dfn[N+5],low[N+5],cnt;
bool cut[N+5];
int dfs(int u,bool k){if(dfn[u]) return dfn[u];dfn[u]=low[u]=++cnt;for(auto&v:a[u])if(!dfn[v]){low[u]=min(low[u],dfs(v,1));if(dfn[u]<=low[v])cut[u]=k,k=1; }else low[u]=min(low[u],dfs(v,1));return low[u];
}
int main(){int n,m;cin>>n>>m;for(int i=1,u,v;i<=m;i++)cin>>u>>v,a[u].push_back(v),a[v].push_back(u);for(int i=1;i<=n;i++) dfs(i,0);cout<<accumulate(cut+1,cut+1+n,0)<<endl;for(int i=1;i<=n;i++)if(cut[i])cout<<i<<' ';
}
无向图的点双连通(v-DCC)分量缩点
点双连通分量有可能有重复的点,因为点双连通分量可能相交于原图的割点。Tarjan求点双连通分量的算法要求出图中点双连通分量包含的点。
流程
求解点双连通分量的过程使用一遍dfs,dfs(u)的过程是:
- 特判掉孤立点
- 访问到以前未被访问的节点 u u u
- 计算 d f n u , l o w u dfn_u,low_u dfnu,lowu
- 把 u u u入栈
- 枚举 u u u的后继 v v v
- 若 v v v未被访问:
递归进 v v v:dfs(v)
更新 l o w u low_u lowu:low[u]=min(low[u],low[v])
若此时满足 d f n u ≤ l o w v dfn_u\leq low_v dfnu≤lowv:则此时栈中从栈顶到 v v v的点,加上点 u u u构成了一个点双连通分量。把栈顶到 v v v之间的点全部弹出,并且统计v-DCC。(是否是点双连通分量与 u u u是否是根节点无关)
一般来说此时还要统计割点,方便缩点。 - 若 v v v已被访问:
更新 l o w u low_u lowu:low[u]=min(low[u],dfn[v])
- 若 v v v未被访问:
然后我们对每个未被访问的点进行dfs,就计算出了全图的SCC情况。
#include<iostream>
#include<vector>
#include<stack>
using namespace std;
const int N=5e5;
vector<int> a[N+5];
int dfn[N+5],low[N+5],cnt;
stack<int>s;
vector<vector<int>>vdcc;
bool cut[N+5];
int dfs(int u,bool k) {if(dfn[u]) return dfn[u];dfn[u]=low[u]=++cnt;s.push(u);for(auto&v:a[u])if(!dfn[v]) {low[u]=min(low[u],dfs(v,1));if(dfn[u]<=low[v]) {cut[u]=k,k=1;先满足dfn[u]<=low[v],再进入统计点双:int x=vdcc.size();vdcc.push_back({});vdcc[x].push_back(u);u属于点双,但是u不出栈。从栈顶到v出栈:while(s.top()^v)vdcc[x].push_back(s.top()),s.pop();vdcc[x].push_back(s.top()),s.pop();}} elselow[u]=min(low[u],dfs(v,1));if(!k) {特判孤立点int x=vdcc.size();vdcc.push_back({});vdcc[x].push_back(u);}return low[u];
}
int main() {int n,m;cin>>n>>m;for(int u,v,i=1;i<=m;i++){cin>>u>>v;a[u].push_back(v);a[v].push_back(u);}for(int i=1;i<=n;i++) dfs(i,0);
}
Tarjan算法求v-DCC的要点主要有四个:
- 额外维护一个栈
- 特判孤立点
- 当 d f n u ≤ l o w v dfn_u\leq low_v dfnu≤lowv时,从栈顶到 v v v的节点+ u u u构成v-DCC,弹出栈顶到 v v v的节点,不弹出 u u u
- 其他部分与求解割点一致(例如更新 l o w u low_u lowu的条件一致)
求出点双连通分量之后我们可以建圆方树:
点双建成方点,枚举一个点双内的所有割点,点双向着割点连接无向边。
证明
证明不易,作者不会。
实现
#include<iostream>
#include<vector>
#include<stack>
using namespace std;
const int N=5e5;
int dfn[N+5],low[N+5],cnt;
stack<int>s;
bool cut[N+5];
vector<int>a[N+5];
vector<vector<int>>vdcc;
int dfs(int u,bool k) {if(dfn[u]) return dfn[u];dfn[u]=low[u]=++cnt;s.push(u);for(auto&v:a[u])if(!dfn[v]) {low[u]=min(low[u],dfs(v,1));if(dfn[u]<=low[v]) {cut[u]=k,k=1;int x=vdcc.size();vdcc.push_back({});vdcc[x].push_back(u);while(s.top()^v)vdcc[x].push_back(s.top()),s.pop();vdcc[x].push_back(s.top()),s.pop();}} elselow[u]=min(low[u],dfs(v,1));if(!k) {int x=vdcc.size();vdcc.push_back({});vdcc[x].push_back(u);}return low[u];
}
int main(){int n,m;cin>>n>>m;for(int u,v,i=1;i<=m;i++)cin>>u>>v,a[u].push_back(v),a[v].push_back(u);for(int i=1;i<=n;i++) dfs(i,0);cout<<vdcc.size()<<endl;for(auto&i:vdcc){cout<<i.size()<<' ';for(auto&j:i)cout<<j<<' ';cout<<endl;}
}
总结
要点
- 强连通性(3)
- 更新条件:未被访问/仍在栈中
- 额外维护栈
- SCC:若 l o w u = d f n u low_u=dfn_u lowu=dfnu,从 u u u到栈顶构成SCC,弹出从 u u u到栈顶的节点并标记。
- 边双连通性(3)
- 更新条件:未被访问/没走反边
- 割边:若 d f n u < l o w v dfn_u<low_v dfnu<lowv,则从 u u u到 v v v走的边是割边
- e-DCC:不走割边形成的连通块,用两遍dfs求解
- 点双连通性(5)
- 更新条件:未被访问/无限制
- 额外维护栈
- 割点: u u u不为根: d f n u ≤ l o w v dfn_u\leq low_v dfnu≤lowv; u u u为根: u u u至少有两个儿子
- v-DCC:若 d f n u ≤ l o w v dfn_u\leq low_v dfnu≤lowv,则点 u u u+栈顶到 v v v的点构成v-DCC,弹出从 v v v到栈顶的点并标记。
- v-DCC需要特判孤立点
代码求出:
- 强连通性
- s c c scc scc数组
- 边双连通性
- c u t cut cut数组(割边)
- 点双连通性
- c u t cut cut数组(割点)以及各个点双连通分量。
代码实现
额外维护
- 强连通性
- 维护栈
- 边双连通性
- 不维护栈
- 点双连通性
- 维护栈
缩点
- 强连通性
- 一遍dfs
- 边双连通性
- 两遍dfs
- 点双连通性
- 一遍dfs
基础实现
Tarjan基础模板:
int dfs(int u) {if(dfn[u]) return dfn[u];dfn[u]=low[u]=++cnt;for(v)if(!dfn[v]) {low[u]=min(low[u],dfs(v));} else if(更新条件) low[u]=min(low[u],dfs(v));return low[u];
}
更新条件:
- 强连通性
- 仍在栈中:
vis[v]
- 仍在栈中:
- 边双连通性
- 未走反边:
pre!=i^1
- 未走反边:
- 点双连通性
- 无限制:
true
- 无限制:
强连通性
判断时机:离开节点时判断SCC
int dfs(int u) {if(dfn[u]) return dfn[u];dfn[u]=low[u]=++cnt;s.push(u);vis[u]=1;for(auto&v:a[u])if(!dfn[v]||vis[v])low[u]=min(low[u],dfs(v));返回前判断:if(dfn[u]==low[u]) {while(s.top()^u)scc[s.top()]=u,vis[s.top()]=0,s.pop();scc[s.top()]=u,vis[s.top()]=0,s.pop();}return low[u];
}
双连通性
判断时机:回到节点时判断割点/割边
进入割点的if语句之后记录点双连通分量。(此时不一定是割点,但一定是点双)
点双要特判孤立点。
int dfs(int u,...) {if(dfn[u]) return dfn[u];dfn[u]=low[u]=++cnt;s.push(u);for(auto&v:a[u])if(!dfn[v]) {low[u]=min(low[u],dfs(v,1));if(割点/割边判断条件) {记录割点/割边记录点双连通分量}} else if()low[u]=min(low[u],dfs(v,1));return low[u];
}
边双连通
int dfs1(int u,int pre){if(dfn[u]) return dfn[u];dfn[u]=low[u]=++cnt;for(int i=h[u],v;(v=to[i]);i=nxt[i])if(!dfn[v])low[u]=min(low[u],dfs1(v,i)),cut[i]=dfn[u]<low[v]; else if(i^pre^1)low[u]=min(low[u],dfs1(v,i));return low[u];
}
vector<int> ans;
bool vis[N+5];
void dfs2(int u){vis[u]=1;ans.push_back(u);for(int i=h[u],v;(v=to[i]);i=nxt[i])if(!vis[v]&&!cut[i])dfs2(v);
}
main():dfs1for(int u=1;u<=n;u++)for(int i=h[u];i;i=nxt[i])if(cut[i])cut[i^1]=1;dfs2点双连通
一遍顶两遍?(雾)
int dfs(int u,bool k) {if(dfn[u]) return dfn[u];dfn[u]=low[u]=++cnt;s.push(u);for(auto&v:a[u])if(!dfn[v]) {low[u]=min(low[u],dfs(v,1));if(dfn[u]<=low[v]) {cut[u]=k,k=1;int x=ans.size();ans.push_back({});ans[x].push_back(u);while(s.top()^v)ans[x].push_back(s.top()),s.pop();ans[x].push_back(s.top()),s.pop();}} elselow[u]=min(low[u],dfs(v,1));if(!k) {int x=ans.size();ans.push_back({});ans[x].push_back(u);}return low[u];
}
后记
求解图连通性的算法有很多种。
例如求解SCC的Kosaraju 算法,Garbow 算法。
求解割边/割点/点双/边双也有其他线性时间复杂度的做法。
于是皆大欢喜。





:话题通信、服务通信的了解和对应节点的搭建(C++))











1)

