文章目录
- 概览:RL方法分类
- 值函数近似(Value function approximation)
- Basic idea
- 目标函数(objective function)
- 优化算法(optimization algorithm)
- Sarsa / Q-learning with function approximation
- Sarsa with function approximation
- Q-learning with function approximation
- 🟦DQN (Deep Q-learning)
- 关键技术1:两个网络
- 关键技术2:经验回放(Experience replay)
- DQN算法步骤(off-policy)
本系列文章介绍强化学习基础知识与经典算法原理,大部分内容来自西湖大学赵世钰老师的强化学习的数学原理课程(参考资料1),并参考了部分参考资料2、3的内容进行补充。
系列博文索引:
- 强化学习的数学原理学习笔记 - RL基础知识
- 强化学习的数学原理学习笔记 - 基于模型(Model-based)
- 强化学习的数学原理学习笔记 - 蒙特卡洛方法(Monte Carlo)
- 强化学习的数学原理学习笔记 - 时序差分学习(Temporal Difference)
- 强化学习的数学原理学习笔记 - 值函数近似(Value Function Approximation)
- 强化学习的数学原理学习笔记 - 策略梯度(Policy Gradient)
- 强化学习的数学原理学习笔记 - Actor-Critic
参考资料:
- 【强化学习的数学原理】课程:从零开始到透彻理解(完结)(主要)
- Sutton & Barto Book: Reinforcement Learning: An Introduction
- 机器学习笔记
*注:【】内文字为个人想法,不一定准确
概览:RL方法分类
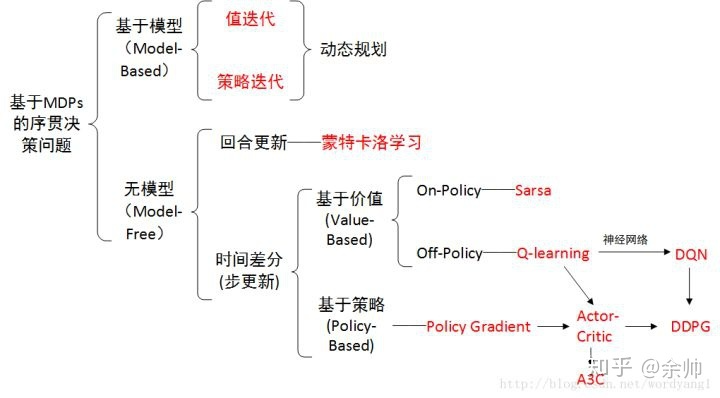
*图源:https://zhuanlan.zhihu.com/p/36494307
值函数近似(Value function approximation)
在先前的方法中,状态/动作值均以表格的(tabular)形式呈现。但是当状态/动作空间较大或者连续时,以上算法会面临存储开销和泛化能力的问题。因此,考虑通过特定函数的形式近似状态值。
Basic idea
*A simple example
假设状态值 v ( s ) v(s) v(s)与状态 s s s之间呈线性关系,设 v ^ ( s , w ) \hat{v}(s, w) v^(s,w)是对 v ( s ) v(s) v(s)的估计,则有下式:
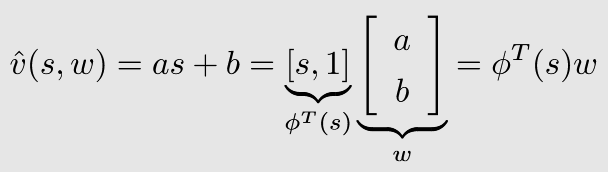
其中, w w w为参数向量, ϕ ( s ) \phi(s) ϕ(s)为状态 s s s的特征向量。
这样做的好处在于大大降低了存储开销:不需要存储每个状态值,只需要存储 w w w(即 a a a和 b b b两个参数)即可。但是弊端在于通过函数近似得到的结果并不一定准确。这种思想可以继续推广到高阶及非线性函数,以提升估计的准确性。
值函数近似的idea:使用参数化(parameterized)的函数近似状态和动作值,即 v ^ ( s , w ) ≈ v π ( s ) \hat{v}(s, w) \approx v_\pi(s) v^(s,w)≈vπ(s),其中 w ∈ R m w \in \mathbb{R}^m w∈Rm是参数向量。
好处:(1) 便于存储:只需要存储参数,不需要存储状态,而参数的维度往往远小于状态的数量;(2) 泛化能力:当访问一个状态后,参数值发生改变,则整个函数估计发生改变,其余未被访问的状态的状态值同样会发生改变,因此不需要访问每个状态来完成学习过程。
目标函数(objective function)
值函数近似的目标是使得估计值尽可能接近真实状态值,其目标函数为:
J ( w ) = E [ ( v π ( S ) − v ^ ( S , w ) ) 2 ] J(w) = \mathbb{E} [ (v_\pi(S) - \hat{v}(S,w))^2 ] J(w)=E[(vπ(S)−v^(S,w))2]
值函数近似的目标,即找到能够使得 J ( w ) J(w) J(w)最小的 w w w。本质上是做策略评估中的状态值估计。
其中, S ∈ S S \in \mathcal{S} S∈S为随机变量,其概率分布为平稳分布(stationary distribution),描述长期行为(long-run behavior),也被称为steady-state distribution或limiting distribution【*一个随机过程/马尔可夫过程中的概念】。直观理解:如果一个agent按照一个给定策略运行了足够久,其马尔可夫过程最终会达到一个平稳状态【即模型(状态转移概率)是稳定的】。
设 { d π ( s ) } s ∈ S \{ d_\pi (s) \}_{s\in \mathcal{S}} {dπ(s)}s∈S表示策略 π \pi π下的马尔可夫过程的平稳分布,有 d π ( s ) ≥ 0 d_\pi (s) \geq 0 dπ(s)≥0且 ∑ s ∈ S d π ( s ) = 1 \textstyle \sum_{s\in \mathcal{S}} d_\pi(s) =1 ∑s∈Sdπ(s)=1。则值函数近似的目标函数可以写作:
J ( w ) = E [ ( v π ( S ) − v ^ ( S , w ) ) 2 ] = ∑ s ∈ S d π ( s ) ( v π ( S ) − v ^ ( S , w ) ) 2 J(w) = \mathbb{E} [ (v_\pi(S) - \hat{v}(S,w))^2 ] = \sum_{s\in \mathcal{S}} d_\pi (s) (v_\pi(S) - \hat{v}(S,w))^2 J(w)=E[(vπ(S)−v^(S,w))2]=s∈S∑dπ(s)(vπ(S)−v^(S,w))2
其中, d π ( s ) d_\pi (s) dπ(s)表示agent处于状态 s s s的概率,同时也是该状态的(重要性)权重值,因此上式可以看作是对不同状态的估计误差的平方的加权平均。
优化算法(optimization algorithm)
采用随机梯度下降(SGD)算法优化(最小化)目标函数 J ( w ) J(w) J(w)(推导过程略):
w t + 1 = w t − α t ( v π ( s t ) − v ^ ( s t , w t ) ) ∇ w v ^ ( s t , w t ) w_{t+1} = w_t - \alpha_t (v_\pi(s_t) - \hat{v}(s_t, w_t)) \nabla_w \hat{v}(s_t, w_t) wt+1=wt−αt(vπ(st)−v^(st,wt))∇wv^(st,wt)
注意到其中 v π ( s t ) v_\pi(s_t) vπ(st)是未知的,其可以用MC或TD近似:
- MC with 值函数近似:用 g t g_t gt(从 s t s_t st出发的累计折扣回报)近似 v π ( s t ) v_\pi(s_t) vπ(st)
- w t + 1 = w t − α t ( g t − v ^ ( s t , w t ) ) ∇ w v ^ ( s t , w t ) w_{t+1} = w_t - \alpha_t (g_t - \hat{v}(s_t, w_t)) \nabla_w \hat{v}(s_t, w_t) wt+1=wt−αt(gt−v^(st,wt))∇wv^(st,wt)
- TD with 值函数近似:用 r t + 1 + γ v ^ ( s t + 1 , w t ) r_{t+1} + \gamma \hat{v}(s_{t+1}, w_t) rt+1+γv^(st+1,wt)近似 v π ( s t ) v_\pi(s_t) vπ(st)
- w t + 1 = w t − α t [ r t + 1 + γ v ^ ( s t + 1 , w t ) − v ^ ( s t , w t ) ] ∇ w v ^ ( s t , w t ) w_{t+1} = w_t - \alpha_t [r_{t+1} + \gamma \hat{v}(s_{t+1}, w_t) - \hat{v}(s_t, w_t)] \nabla_w \hat{v}(s_t, w_t) wt+1=wt−αt[rt+1+γv^(st+1,wt)−v^(st,wt)]∇wv^(st,wt)
- TD target: r t + 1 + γ v ^ ( s t + 1 , w t ) r_{t+1} + \gamma \hat{v}(s_{t+1}, w_t) rt+1+γv^(st+1,wt)
- *实际上这种方法并不是在优化原本的目标函数,而是在优化另一个相关的目标函数,称作projected Bellman error(详细内容略)
- w t + 1 = w t − α t [ r t + 1 + γ v ^ ( s t + 1 , w t ) − v ^ ( s t , w t ) ] ∇ w v ^ ( s t , w t ) w_{t+1} = w_t - \alpha_t [r_{t+1} + \gamma \hat{v}(s_{t+1}, w_t) - \hat{v}(s_t, w_t)] \nabla_w \hat{v}(s_t, w_t) wt+1=wt−αt[rt+1+γv^(st+1,wt)−v^(st,wt)]∇wv^(st,wt)
v ^ ( s , w ) \hat{v} (s, w) v^(s,w)的形式选择:早期用线性函数,目前通用神经网络(Neural Network,NN)来拟合未知非线性函数。线性函数的好处在于其理论性非常容易分析,弊端在于其特征向量(比如其阶数)难以选择。
*若 v ^ ( s , w ) \hat{v} (s, w) v^(s,w)为线性函数,则其等价于tabular representation,因此可以将tabular representation看作linear function approximation的一种特殊情况。
Sarsa / Q-learning with function approximation
Sarsa with function approximation
其实就是把TD with function approximation中的状态值换为动作值:
w t + 1 = w t + α t [ r t + 1 + γ q ^ ( s t + 1 , a t + 1 , w t ) − q ^ ( s t , a t , w t ) ] ∇ w q ^ ( s t , a t , w t ) w_{t+1} = w_t + \alpha_t [r_{t+1} + \gamma \hat{q}(s_{t+1}, a_{t+1}, w_t) - \hat{q}(s_t, a_t, w_t)] \nabla_w \hat{q}(s_t, a_t, w_t) wt+1=wt+αt[rt+1+γq^(st+1,at+1,wt)−q^(st,at,wt)]∇wq^(st,at,wt)
和Tabular Sarsa的区别:不是直接更新动作值 q ( s , a ) q(s,a) q(s,a),而是更新参数值 w w w。
采用ε-Greedy方法进行策略提升:
π k + 1 ( a ∣ s t ) = { 1 − ε ∣ A ( s ) ∣ ( ∣ A ( s ) ∣ − 1 ) if a = arg max a ∈ A ( s t ) q ^ ( s t , a , w t + 1 ) ε ∣ A ( s ) ∣ otherwise \pi_{k+1}(a|s_t) = \begin{cases} 1-\frac{\varepsilon}{|\mathcal{A} (s)|} (|\mathcal{A}(s)|-1) &\text{if } a = \argmax_{a\in\mathcal{A(s_t)}} \hat{q}(s_t, a, w_{t+1}) \\ \frac{\varepsilon}{|\mathcal{A}(s)|} &\text{otherwise} \end{cases} πk+1(a∣st)={1−∣A(s)∣ε(∣A(s)∣−1)∣A(s)∣εif a=argmaxa∈A(st)q^(st,a,wt+1)otherwise
注意其中的 q ^ ( s t , a , w t + 1 ) \hat{q}(s_t, a, w_{t+1}) q^(st,a,wt+1)需要通过函数计算得到。
Q-learning with function approximation
w t + 1 = w t + α t [ r t + 1 + γ max a ∈ A ( s t + 1 ) q ^ ( s t + 1 , a t , w t ) − q ^ ( s t , a t , w t ) ] ∇ w q ^ ( s t , a t , w t ) w_{t+1} = w_t + \alpha_t [r_{t+1} + \gamma {\color{red} \max_{a \in \mathcal{A}(s_{t+1})} \hat{q}(s_{t+1}, a_{t}, w_t)} - \hat{q}(s_t, a_t, w_t)] \nabla_w \hat{q}(s_t, a_t, w_t) wt+1=wt+αt[rt+1+γa∈A(st+1)maxq^(st+1,at,wt)−q^(st,at,wt)]∇wq^(st,at,wt)
🟦DQN (Deep Q-learning)
尽管在Q-learning with function approximation中,可以使用神经网络作为 q ^ ( s , a , w ) \hat{q} (s, a, w) q^(s,a,w),但其需要复杂的底层运算(如求梯度),因此提出了DQN(Deep Q-learning / Deep Q Network)作为替代。
DQN的目标函数/损失(loss)函数:
J ( w ) = E [ ( R + γ max α ∈ A ( S ′ ) q ^ ( S ′ , a , w ) − q ^ ( S , A , w ) ) 2 ] J(w) = \mathbb{E} \Big[ \Big(R + \gamma \max_{\alpha \in \mathcal{A} (S') } \hat{q} (S', a, w) - \hat{q} (S, A ,w) \Big) ^2 \Big] J(w)=E[(R+γα∈A(S′)maxq^(S′,a,w)−q^(S,A,w))2]
其中, ( S , A , R , S ′ ) (S,A,R,S') (S,A,R,S′)均为随机变量, R + γ max α ∈ A ( S ′ ) q ^ ( S ′ , a , w ) − q ^ ( S , A , w ) R + \gamma \max_{\alpha \in \mathcal{A} (S') } \hat{q} (S', a, w) - \hat{q} (S, A ,w) R+γmaxα∈A(S′)q^(S′,a,w)−q^(S,A,w)为Q-learning的TD error,也即Bellman optimlity error,当该值为0时取得最优。
关键技术1:两个网络
直接采用梯度下降优化损失函数并不容易,因为其中两项都包含 w w w,求梯度较复杂。一个简单的思路是,将 y = R + γ max α ∈ A ( S ′ ) q ^ ( S ′ , a , w ) y = R + \gamma \textstyle \max_{\alpha \in \mathcal{A} (S') } \hat{q} (S', a, w) y=R+γmaxα∈A(S′)q^(S′,a,w)视作常数,只需求解 q ^ ( S , A , w ) \hat{q} (S, A ,w) q^(S,A,w)的梯度即可。
因此,DQN引入了两个网络的设计:
- main network:对应 q ^ ( S , A , w ) \hat{q} (S, A ,w) q^(S,A,w)
- target network:对应 q ^ ( S ′ , a , w T ) \hat{q} (S', a, w_T) q^(S′,a,wT)
main network的参数 w w w实时更新,但target network的参数 w T w_T wT并非实时更新,而是隔一段时间把main network的 w w w赋值过来,因此在这段时间内, w T w_T wT可以被视为常数。
DQN的basic idea:使用梯度下降(GD)优化损失函数,对应梯度为:
∇ w J = E [ ( R + γ max α ∈ A ( S ′ ) q ^ ( S ′ , a , w T ) − q ^ ( S , A , w ) ) ∇ w q ^ ( S , A , w ) ] \nabla_w J = \mathbb{E} \Big[ \Big(R + \gamma \max_{\alpha \in \mathcal{A} (S') } {\color{red} \hat{q} (S', a, w_T) } - {\color{blue} \hat{q} (S, A ,w) } \Big) {\color{blue} \nabla_w \hat{q} (S, A ,w) } \Big] ∇wJ=E[(R+γα∈A(S′)maxq^(S′,a,wT)−q^(S,A,w))∇wq^(S,A,w)]
训练过程(详见下):在每次迭代中,DQN从回放缓存(replay buffer)中取mini-batch采样 { ( s , a , r , s ′ ) } \{(s, a, r, s')\} {(s,a,r,s′)},以 s s s和 a a a作为输入计算得到 y T = r + γ max α ∈ A ( s ′ ) q ^ ( s ′ , a , w T ) y_T = r + \gamma \textstyle \max_{\alpha \in \mathcal{A} (s') } \hat{q} (s', a, w_T) yT=r+γmaxα∈A(s′)q^(s′,a,wT),并基于mini-batch { ( s , a , y T ) } \{ (s, a, y_T) \} {(s,a,yT)}最小化损失函数 ( y T − q ^ ( s , a , w ) ) 2 ( y_T - \hat{q} (s, a ,w) )^2 (yT−q^(s,a,w))2以训练main network。之后,将main network的参数 w w w赋值给target network的 w T w_T wT。
关键技术2:经验回放(Experience replay)
DQN在收集经验采样后,将其存储在回放缓存(replay buffer) B = { ( s , a , r , s ′ ) } \mathcal{B} = \{ (s, a, r, s') \} B={(s,a,r,s′)}中。当需要使用采样训练神经网络时,从回放缓存中按照均匀分布(uniform distribution)随机取mini-batch的采样 ,该过程称为经验回放。
- 均匀分布:对所有 ( s , a ) (s, a) (s,a)对等概率访问(不等概率的话,需要先验知识才能确定哪些 ( s , a ) (s, a) (s,a)对更重要)
- 这里是把 ( S , A ) (S,A) (S,A)对看作一个随机变量
- 回放缓存:经验采样的采集有先后顺序,直接按照其顺序使用可能不满足均匀分布的要求,因此将过往经验先存起来再均匀采样,去除采样间的相关性
*实际上经验回放也可以用于tabular Q-learning中,还能提高其采样效率(因为可以重复利用)。
DQN算法步骤(off-policy)
目标:从行为策略 π b \pi_b πb生成的经验采样中,学习一个最优的target network以近似最优动作值
在每次迭代中:
- 从回放缓存 B \mathcal{B} B中均匀取mini-batch采样
- 对于每个采样 ( s , a , r , s ′ ) (s, a, r, s') (s,a,r,s′),计算 y T = r + γ max α ∈ A ( s ′ ) q ^ ( s ′ , a , w T ) y_T = r + \gamma \textstyle \max_{\alpha \in \mathcal{A} (s') } \hat{q} (s', a, w_T) yT=r+γmaxα∈A(s′)q^(s′,a,wT),其中 w T w_T wT为target network的参数
- 使用mini-batch采样 { ( s , a , y T ) } \{ (s, a, y_T) \} {(s,a,yT)}更新main network,以最小化损失函数 ( y T − q ^ ( s , a , w ) ) 2 ( y_T - \hat{q} (s, a ,w) )^2 (yT−q^(s,a,w))2
每 C C C次迭代后,将 w w w赋值给 w T w_T wT。
*注意:这里的表述与DQN原论文不同(原论文的NN更高效),但本质是一样的。
![JS输出为[object object]取值问题](http://pic.xiahunao.cn/JS输出为[object object]取值问题)






 fatal: index-pack 失败)










流 list转map)
