前言

我们可能没有在瑞士苏黎世银行存入巨额资产的机会，但相信大多数人都在电影中见到这样一组镜头：

户主带着自己的钥匙来到银行，要求取出自己寄放的物品。银行工作人员验明户主身份后，拿出另一把钥匙同户主一起打开保险柜，将用户寄放物品取出。我们可以把这个保险柜称为“双钥保险柜”。

要开启双钥保险柜同时需要两把钥匙。一把钥匙留给户主，由户主保管，我们可以把它叫做公钥。另一把钥匙留给银行，由银行保管，我们可以把它叫做私钥。

将上述内容引申为加密/解密应用，我们就能体会到非对称加密算法与对称加密算法之间的区别。

对称加密算法仅有一个密钥，既可用于加密，亦可用于解密若完成加密/解密操作，仅需要一个密即可。

而非对称加密算法拥有两个密钥一个用于加密，另一个则用于解密。若要完成加密/解密操作，需要两个密钥同时参与。

相比与对称加密算法的单钥体系，非对称加密算法的双钥体系就更为安全。但非对称加密的缺点是加解密速度要远远慢于对称加密，在某些极端情况下，非对称加密算法甚至比非对称加密要慢1000倍。

非对称加密算法的由来

密钥管理是对称加密算法系统不容忽视的问题，它成为安全系统中最为薄弱的环节。为了弥补这一弱势，非对称加密算法应运而生。

1976年，W.Diffie和M.Hellman在IEEE (Institute of Electrical and Electronics Engineers，美国电气和电子工程师协会)的刊物上发表《密码学的新方向》文，首次提出非对称加密算法。

非对称加密算法有别于对称加密算法，将密钥一分为二，公钥公开，私钥保密。

公钥通过非安全通道发放，私钥则由发放者保留。公钥与私钥相对应，成对出现。公钥加密的数据，只可使用私钥对其解密。反之，私加密的数据，只可使用公钥对其解密。

非对称加密算法与对称加密算法相比，密钥管理问题不复存在，在安全性上有着无法逾越的高度，但却无法回避加密/解密效率低这一问题。因此，非对称加密算法往往应用在一些安全性要求相当高的领域，如B2C、B2B等电子商务平台。

注意：
针对非对称加密算法的低效问题，各密码学机构主张将对称加密算法与非对称加密算法相结合，使用对称加密算法为数据加密/解密，使用公钥和私钥为对称加密算法密钥加密/解密。

利用对称加密算法的高效性，加之非对称加密算法的密钥管理，提升整体加密系统的安全性。

在算法设计上，非对称加密算法对待加密数据长度有着极为苛刻的要求。

例如，RSA算法要求待加密数据不得大于53个字节，非对称加密算法主要用于交换对称加密算法的秘密密钥，而非数据交换。

非对称加密算法的家谱

非对称加密算法源于DH算法 (Diffie-Hellman，密钥交换算法)，由W.Diffie和M.Hellman共同提出。该算法为非对称加密算法奠定了基础，堪称非对称加密算法之鼻祖。

DH算法提出后，国际上相继出现了各种实用性更强的非对称加密算法，其构成主要是基于数学问题的求解，主要分为两类：

1.基于因子分解难题

RSA算法是最为典型的非对称加密算法，该算法由美国麻省理工学院(MIT)的Ron Rivest、AdiShamir和Leonard Adleman三位学者提出，并以这三位学者的姓氏开头字母命名，称为RSA算法。

RSA算法是当今应用范围最为广泛的非对称加密算法，也是第一个既能用于数据加密也能用于数字签名的算法。

2.基于离散对数难题

EIGamal算法由Taher EIGamal提出，以自己的名字命名。该算法即可用于加密/解密，也可用于数字签名，并为数字签名算法形成标准提供参考。

美国的DSS( Digital Signature Standard，数据签名标准)的DSA ( Digital SignatureAlgorithm，数字签名算法)经EIGamal算法演变而来。

ECC (Elliptical Curve Cryptography，圆曲线加密)算法以圆曲线理论为基础，在创建密钥时可做到更快、更小，并且更有效。

ECC 算法通过圆曲线方程式的性质产生密钥，而不是采用传统的方法利用大质数的积来产生。

密钥交换算法-DH

对称加密算法提高数据安全性的同时带来了密钥管理的复杂性。

消息收发双方若想发送加密消息，必须事先约定好加密算法并发放密钥。而如何安全的传递密钥，成为对称加密算法的一个棘手问题。密钥交换算法 (Diffie-Hellman算法，简称DH算法)成为解决这一问题的金钥匙!

1976年，W.Diffie和MHellman在发表的论文中提出了公钥加密算法思想，但当时并没有给出具体的实施方案，原因在于没有找到单向函数(也就是消息摘要算法)，但在该文中给出了通信双方通过信息交换协商密钥的算法，即Diffie-Hellman密钥交换算法(通常简称为DH算法)。

该算法的目的在于让消息的收发双方可以在安全的条件下交换密钥，以备后续加密/解密使用。因此，DH算法是第一个密钥协商算法，但仅能用于密钥分配，不能用于加密或解密消息。

DH密钥交换算法的安全性基于有限域上的离散对数难题。基于这种安全性，通过DH算法进行密钥分配，使得消息的收发双方可以安全地交换一个秘密密钥，再通过这个密钥对数据进行加密和解密处理。

密钥交换算法-DH的通信模型

以消息传递模型为例，甲方作为发送者，乙方作为接收者。
下面分析甲乙双方如何构建密钥、交互密钥和加密数据。

初始化DH算法密钥对

甲乙两方构建密钥需要经过以下几个步骤：

1)由消息发送的一方构建密钥，这里由甲方构建密钥

2)由构建密钥的一方向对方公布其公钥，这里由甲方向乙方发布公钥

3)由消息接收的一方通过对方公钥构建自身密钥，这里由乙方使用甲方公钥构建乙方密钥。

4)由消息接收的一方向对方公布其公钥，这里由乙方向甲方公布公钥

这里要注意的是，乙方构建自己的密钥对的时候需要使用甲方公钥作为参数。这是很关键的一点，如果缺少了这一环节则无法确保甲乙双方获得同一个秘密密钥，消息加密更无从谈起。

假设甲乙双方事先约定好了用于数据加密的对称加密算法(如AES算法)并构建本地密钥 (即对称加密算法中的秘密密钥)，

甲方构建DH算法本地密钥

甲方需要使用自己的私钥和乙方的公钥才能构建本地密钥，即用于数据加密/解密操作的对称加密算法的秘密密钥。

乙方构建DH算法本地密钥

乙方构建本地密钥的方式与甲方相类似，同样需要通过使用自己的私钥和甲方的公钥构建本地密钥。

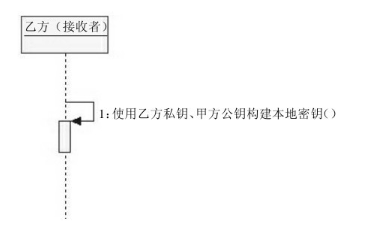
虽然甲乙两方使用了不同的密钥来构建本地密钥，但甲乙两方得到密钥其实是一致的。也正因于此，甲乙双方才能顺利地进行加密消息的传递。

DH算法加密消息传递

最后，甲乙双方构建了本地密钥后，可按基于对称加密算法的消息传递模型完成消息传递。如图：

作为对称加密体制向非对称加密体制的一种过渡，DH算法仅仅比一般的对称加密算法多了密钥对的构建和本地密钥的构建这两项操作，而真正的数据加密/解密操作仍由对称加密算法完成。

典型非对称加密算法-RSA

DH算法的诞生为后续非对称加密算法奠定了基础，较为典型的对称加密算法(如EIGamal、RSA和ECC算法等)都是在DH算法提出后相继出现的，并且其算法核心都源于数学问题。

RSA算法基于大数因子分解难题，而ElGamal算法和ECC算法则是基于离散对数难题。

目前，各种主流计算机语言都提供了对RSA算法的支持。

1978年，美国麻省理工学院(MIT)的Ron Rivest、 Adi Shamir和LeonardAdleman三位学者提出了一种新的非对称加密算法，这种算法以这三位学者的姓氏开头字母命名，被称为RSA算法。

RSA算法是唯一被广泛接受并实现的通用公开加密算法，目前已经成为非对称加密算法国际标准。不仅如此，RSA算法既可用于数据加密也可用于数字签名。

RSA算法将非对称加密算法推向了一个高潮，但它并不是没有缺点。相比DES以及其他对称加密算法而言，RSA算法要慢得多。作为加密算法，尤其是作为非对称加密算法的典型，针对RSA算法的破解自诞生之日起就从未停止过。

RSA的通信模型

通过了解基于DH算法的消息传递模型，我们更容易理解基于非对称加密算法的消息传递模型的工作方式。或者说，基于DH算法的消息传递模型更为底层。

RSA算法代表了真正的非对称加密算法，其操作较之DH算法较为简单在构建密钥对方面，RSA算法就相当简单。

我们仍以甲乙两方收发消息为例。

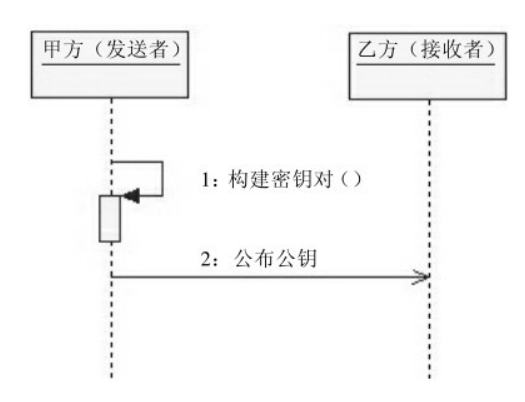
甲方作为消息的发送方，乙方作为消息的接收方。我们假设甲乙双方在消息传递之前已将RSA算法作为消息传递的加密算法。为完成加密消息传递，甲乙双方需要以下操作：

1. 由消息发送的一方构建密钥对，这里由甲方完成

2. 由消息发送的一方公布公钥至消息接收方，这里由甲方将公钥公布给乙方。

完成这两步操作后，甲乙双方就可以进行加密消息传递了，如图：

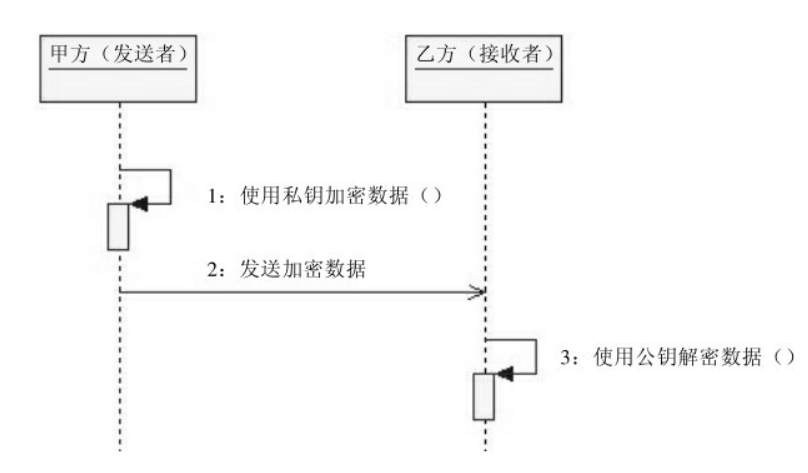
这里需要读者朋友注意：
甲方向乙方发送数据时，使用私钥对数据做加密处理；乙方接收到加密数据后，使用公钥对数据做解密处理。

在非对称加密算法领域中，对于私钥加密的数据，只能使用公钥解密。简言之，“私钥加密，公钥解密”。

RSA特有的的“公钥加密，私钥解密”

相对于“私钥加密，公钥解密”的实现，RSA算法提供了另一种加密/解密方式：“公钥加密，私钥解密”。

这使得乙方可以使用公钥加密数据，如图：

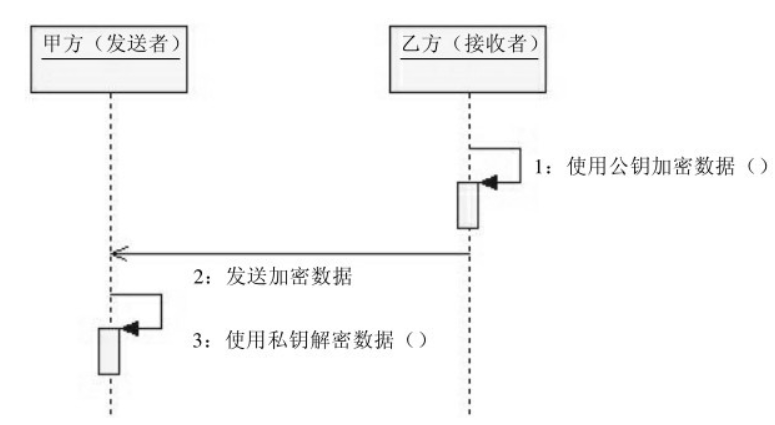
“公钥加密，私钥解密”是否可取？

用公钥加密数据的方式是否可取呢?

公钥是通过甲方发送给乙方的，其在传递过程中很有可能被截获，也就是说窃听者很有可能获得公钥。

如果窃听者获得了公钥，向甲方发送数据，甲方是无法辨别消息的真伪的。

因此，虽然可以使用公钥对数据加密，但这种方式还是会有存在-定的安全隐患。

如果要建立更安全的加密消息传递模型，就需要甲乙两方构建两套非对称加密算法密钥，仅遵循“私钥加密，公钥解密”的方式进行加密消息传递。

RSA算法和DH算法的区别和联系

RSA算法实现较之DH算法实现较为简单，大部分内容与DH算法较为接近。与DH算法不同的是，RSA算法仅需要一套密钥即可完成加密/解密操作。

常见使用场景

非对称加密在信息安全领域中有许多常用场景，其中一些主要的应用包括：

1. 安全通信： 非对称加密用于安全地传输密钥以保护对称加密通信。在SSL/TLS协议中，服务器和客户端使用非对称加密（如RSA）协商会话密钥，然后使用对称加密算法来加密实际数据传输。

2. 数字签名： 非对称加密用于生成和验证数字签名，以确保数据的完整性和真实性。发送者使用私钥对数据签名，而接收者使用公钥来验证签名，从而确认数据未被篡改且确实由特定发送者生成。

3. 身份验证： 非对称加密用于实现安全身份验证。例如，SSH（Secure Shell）协议使用非对称加密来进行客户端和服务器之间的身份验证，确保只有授权的用户可以远程登录。

4. 数字证书： 非对称加密在数字证书中发挥关键作用。数字证书包含了公钥，用于证明实体的身份。这在Web浏览器和服务器之间建立安全连接时特别重要，例如在HTTPS通信中。

5. 密钥交换： 非对称加密用于安全地交换密钥。例如，Diffie-Hellman密钥交换协议使用非对称加密来协商密钥，使得通信双方可以安全地共享密钥而不必在通信通道上传输密钥。

6. 加密文件和存储： 非对称加密可以用于加密文件和数据，以确保只有拥有私钥的用户能够解密和访问数据。这提供了对数据隐私的保护，即使公钥是公开的。

7. 电子邮件加密： 非对称加密可用于电子邮件加密，确保只有目标收件人能够解密和阅读电子邮件内容。PGP（Pretty Good Privacy）是一个常见的使用非对称加密的电子邮件加密协议。

这些场景突显了非对称加密在建立安全通信、保护数据完整性和实现身份验证方面的重要性。

总结

在实际应用中，我们很少会直接使用非对称加密算法进行数据加密。真正对数据进行加密的算法其实都是对称加密算法。非对称加密算法的主要职责是用来初始化对称加密算法的秘密密钥。

这里，其实在真正的项目实战中，我们缺少了对于数据校验的部分。

对于这项关键操作我们有两种选择：

1. 使用消息摘要算法对其数据进行摘要/验证
2. 使用数字签名对其数据进行签名/验证

非对称加密算法通常配合数字证书、SSL/TLS协议构建单向认证或双向认证使用。

参考资料

《Java加密与解密艺术》