写在前面:
(1)建议看这篇论文之前,可先看我写的前一篇论文:
DDPM推导笔记-大白话推导
主要学习和参考了以下文章:
(1)一文带你看懂DDPM和DDIM
(2)关于 DDIM 采样算法的推导
0. DDIM的创新点
DDPM有一个很大的缺点就是其本身是一个马尔科夫链的过程,推理速度太慢,如果前向加噪过程是1000步,那么去噪过程就需要使用Unet生成噪声,然后去噪,这样进行1000步。这是一个及其缓慢的过程,DDIM原论文中举了一个生动的例子:
For example, it takes around 20 hours to sample 50k images of size 32 x 32 from a DDPM, but less than a minute to do so from a GAN on a Nvidia 2080 Ti GPU.
基于DDPM,DDIM主要有两项改进:
(1)对于一个已经训练好的DDPM,只需要对采样公式做简单的修改,模型就能在去噪时「跳步骤」,在一步去噪迭代中直接预测若干次去噪后的结果。比如说,假设模型从时刻T=100开始去噪,新的模型可以在每步去噪迭代中预测10次去噪操作后的结果,也就是逐步预测时刻t=90,80,…,0的结果。这样,DDPM的采样速度就被加速了10倍。
(2)DDIM论文推广了DDPM的数学模型,打破了马尔科夫链的过程,从更高的视角定义了DDPM的反向过程(去噪过程)。在这个新数学模型下,我们可以自定义模型的噪声强度,让同一个训练好的DDPM有不同的采样效果。
1. 公式推导
DDPM的推导过程可以看《DDPM推导笔记》,这里假设 P ( x t − 1 ∣ x t , x 0 ) P(x_{t-1}|x_t, x_0) P(xt−1∣xt,x0)满足如下正态分布,即:
P ( x t − 1 ∣ x t , x 0 ) ∼ N ( k x 0 + m x t , σ 2 ) 即 : x t − 1 = k x o + m x t + σ ϵ 其中有: ϵ ∼ N ( 0 , 1 ) (1) P(x_{t-1}|x_t, x_0) \sim N(kx_0+mx_t, \sigma^2) \\ 即:x_{t-1} = kx_o+mx_t + \sigma \epsilon \tag{1} \\ 其中有: \epsilon \sim N(0, 1) P(xt−1∣xt,x0)∼N(kx0+mxt,σ2)即:xt−1=kxo+mxt+σϵ其中有:ϵ∼N(0,1)(1)
又因为前向的加噪过程满足:
x t = a t ˉ x 0 + 1 − a t ˉ ϵ 其中 ϵ ∼ N ( 0 , 1 ) (2) x_t = \sqrt{\bar{a_t}} x_0 + \sqrt{1 - \bar{a_t}} \epsilon \\ 其中\epsilon \sim N(0,1) \tag{2} xt=atˉx0+1−atˉϵ其中ϵ∼N(0,1)(2)
合并(1)(2)上面两式,有:
x t − 1 = k x 0 + m [ a ˉ t x 0 + 1 − a ˉ t ϵ ] + σ ϵ (3) x_{t-1} = kx_0 + m[\sqrt{\bar{a}_t}x_0 + \sqrt{1-\bar{a}_t} \epsilon] + \sigma \epsilon \tag{3} xt−1=kx0+m[aˉtx0+1−aˉtϵ]+σϵ(3)
再次合并有:
x t − 1 = ( k + m a ˉ t ) x 0 + ϵ ′ 其中: ϵ ’ ∼ M ( 0 , m 2 ( 1 − a ˉ t ) + σ 2 ) (4) x_{t-1} = (k+m\sqrt{\bar{a}_t}) x_0 + \epsilon' \\ 其中: \epsilon’ \sim M(0, m^2(1-\bar{a}_t) + \sigma^2) \tag{4} xt−1=(k+maˉt)x0+ϵ′其中:ϵ’∼M(0,m2(1−aˉt)+σ2)(4)
从DDPM中可以可知:
x t − 1 = a ˉ t − 1 x 0 + 1 − a ˉ t − 1 ϵ (5) x_{t-1} = \sqrt{\bar{a}_{t-1}} x_0 + \sqrt{1-\bar{a}_{t-1}} \epsilon \tag{5} xt−1=aˉt−1x0+1−aˉt−1ϵ(5)
通过式(4)(5)的 x t − 1 x_{t-1} xt−1服从的概率分布可知:
k + m a ˉ t = a ˉ t − 1 m 2 ( 1 − a ˉ t ) + σ 2 = 1 − a ˉ t − 1 (6) k + m\sqrt{\bar{a}_t} = \sqrt{\bar{a}_{t-1}} \\ m^2(1-\bar{a}_t) + \sigma^2 = 1-\bar{a}_{t-1} \tag{6} k+maˉt=aˉt−1m2(1−aˉt)+σ2=1−aˉt−1(6)
由式(6)两个式子可解出:
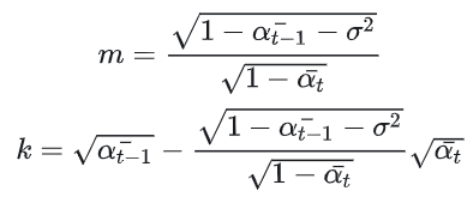
将m,k带入到 P ( x t − 1 ∣ x t , x 0 ) P(x_{t-1}|x_t, x_0) P(xt−1∣xt,x0)中,可得:
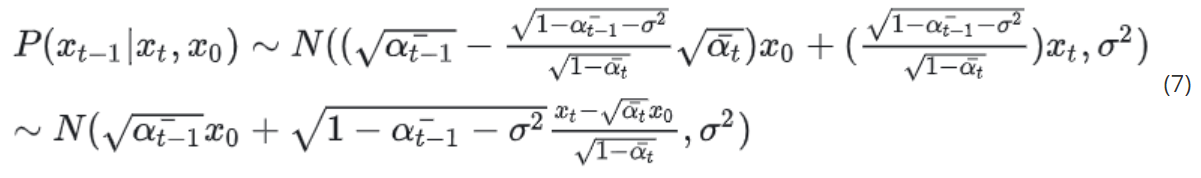
依旧可以使用 x t , x 0 x_t, x_0 xt,x0的关系式把 x 0 x_0 x0去掉:
x t = a t ˉ x 0 + 1 − a t ˉ ϵ 这里为了防止 ϵ 和后面的 ϵ 搞混,这里记为 ϵ t , 则上式变为: x t = a t ˉ x 0 + 1 − a t ˉ ϵ t (8) x_t = \sqrt{\bar{a_t}} x_0 + \sqrt{1 - \bar{a_t}} \epsilon \\ 这里为了防止\epsilon和后面的\epsilon搞混,这里记为\epsilon_{t},则上式变为:\\ x_t = \sqrt{\bar{a_t}} x_0 + \sqrt{1 - \bar{a_t}} \epsilon_t \tag{8} xt=atˉx0+1−atˉϵ这里为了防止ϵ和后面的ϵ搞混,这里记为ϵt,则上式变为:xt=atˉx0+1−atˉϵt(8)
从 P ( x t − 1 ∣ x t , x 0 ) P(x_{t-1}|x_t, x_0) P(xt−1∣xt,x0)的概率分布采样可得到:
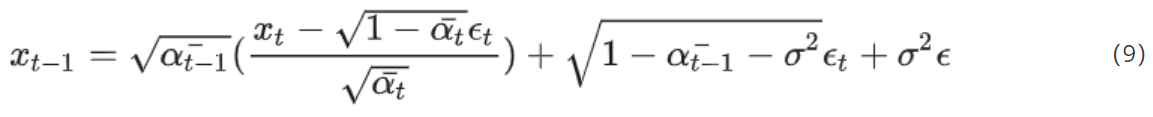
其中, ϵ \epsilon ϵ是从标准正太分布中,随机采样得到; ϵ t \epsilon_t ϵt是和DDPM一样,使用神经网络训练而来的; x t x_t xt是输入; a ˉ t − 1 和 a ˉ t \bar{a}_{t-1}和\bar{a}_t aˉt−1和aˉt是事先定义好的。至此,我们就只需要讨论 σ \sigma σ这个参数了。
2. σ \sigma σ的讨论
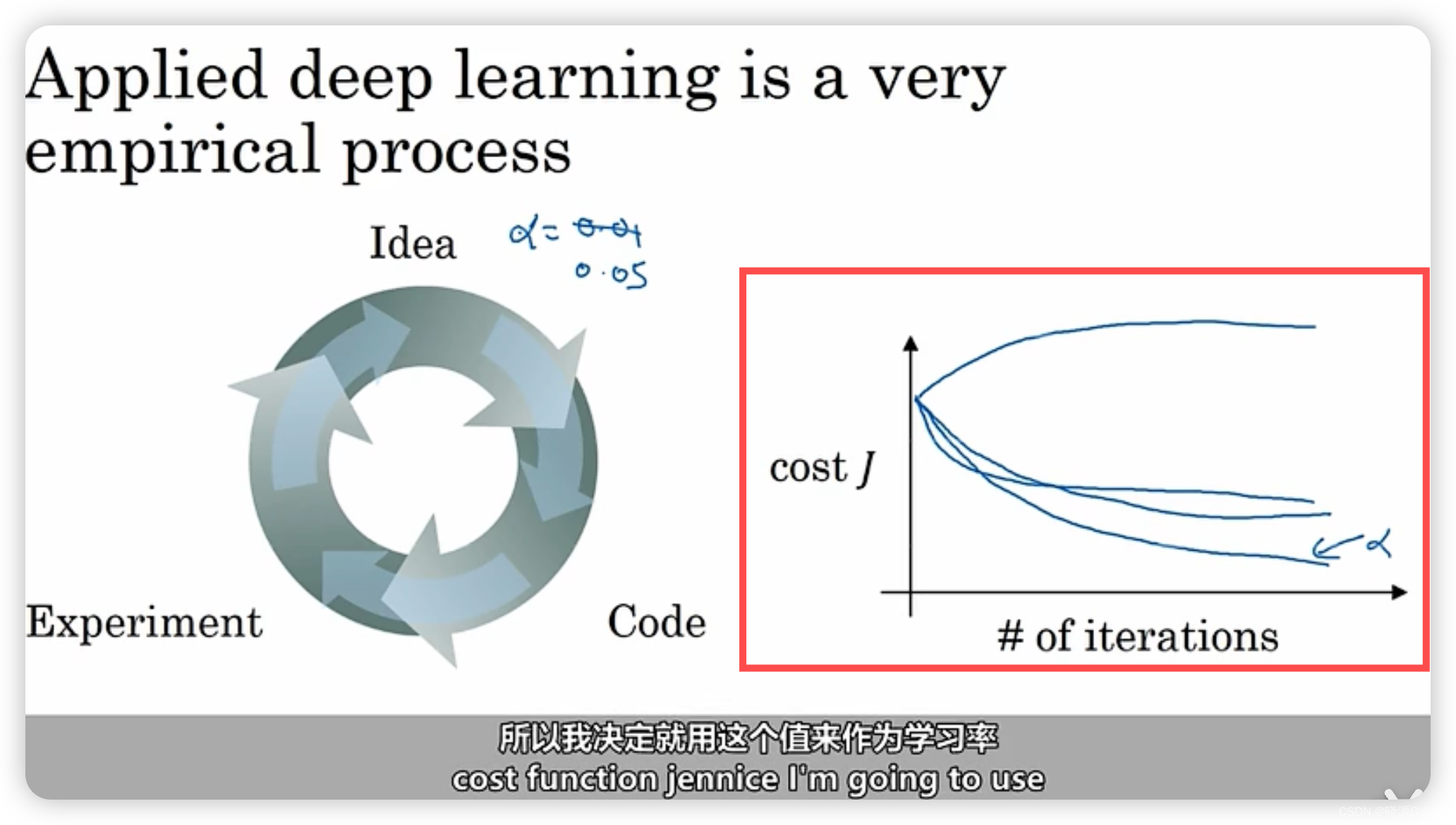
怎样选取 σ \sigma σ才能获得最佳的加速效果呢?
作者做了一些实验,作者原文中使用 σ τ i ( η ) \sigma_{\tau_i}{(\eta)} στi(η)来表示的 σ \sigma σ,其式子如下:
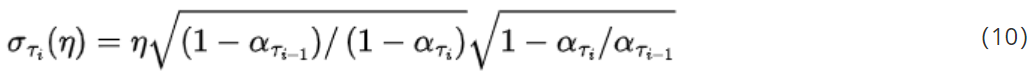
使用 η \eta η控制其大小。事实上,当 η = 1 \eta = 1 η=1时就变成了DDPM的去噪过程了,
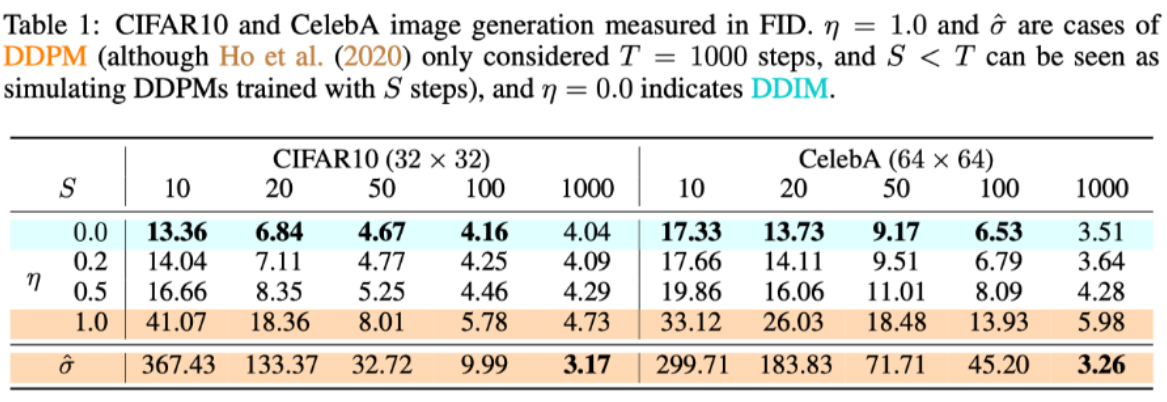
当 η = 0 \eta=0 η=0时,效果是最好的。所以DDIM令 σ = 0 \sigma=0 σ=0。
3. x p r e v x_{prev} xprev的推导
从式9且 σ = 0 \sigma=0 σ=0,则式9中的所有都已知了!!!
但是,即使这样,我们也还是由 x t 推导出 x t − 1 x_t推导出x_{t-1} xt推导出xt−1呀,这样还是不能加快推理!
不忙,我们回过头去思考,发现上面的推导过程中全程没有使用:
x t = a t x t − 1 + 1 − a t ϵ x_t= \sqrt{a_t}x_{t-1} + \sqrt{1-a_t} \epsilon xt=atxt−1+1−atϵ
也就可以不需要严格的由 x t 算到 x t − 1 x_t算到x_{t-1} xt算到xt−1,则可以令 x p r e v 替代 x t − 1 x_{prev}替代x_{t-1} xprev替代xt−1,式(9)则可以变换为:
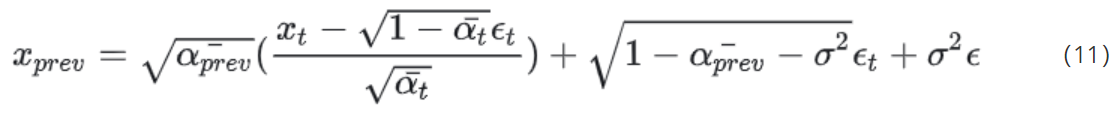
至此,所有的参数要是实现定义好了,要么是需要训练的,这样 x t 和 x p r e v x_t和x_{prev} xt和xprev则可以相隔多个迭代步数。
4.疑难解答
Q1: 为什么式(11)可以简单的将 x p r e v 替代 x t − 1 x_{prev}替代x_{t-1} xprev替代xt−1,毕竟虽然反向过程没有使用到 x t − 1 算到 x t x_{t-1}算到x_{t} xt−1算到xt的关系式,但前向过程是使用到的呀?
目前我也没有答案!还在理解中,由大佬路过,请留言讨论!
Q2: 为什么在DDIM可以令方差 σ = 0 \sigma=0 σ=0 ?
目前我也没有答案!还在理解中,由大佬路过,请留言讨论!