一、径向基函数的定义
如果 ∣ ∣ x 1 ∣ ∣ = ∣ ∣ x 2 ∣ ∣ ||x_1||=||x_2|| ∣∣x1∣∣=∣∣x2∣∣,那么 ϕ ( x 1 ) = ϕ ( x 2 ) \phi(x_1)=\phi(x_2) ϕ(x1)=ϕ(x2) 的函数 ϕ \phi ϕ 就是径向函数,即仅由 r = ∣ ∣ x ∣ ∣ r=||x|| r=∣∣x∣∣ 控制的函数(径向基函数是一个取值仅仅依赖于离原点距离的实值函数,或者还可以是到任意一点 c c c 的距离)。
给定一个一元函数 ϕ : R + → R \phi:R_+\rightarrow R ϕ:R+→R,在定义域 x ∈ R d x\in R^d x∈Rd 上,所有形如 ψ ( x ) = ϕ ( ∣ ∣ x − c ∣ ∣ ) \psi(x)=\phi(||x-c||) ψ(x)=ϕ(∣∣x−c∣∣) 及其线性组合张成的函数空间称为由函数 ϕ \phi ϕ 导出的径向基函数空间。
在一定的条件下,只要取 { x j } \{x_j\} {xj} 两两不同, { ϕ ( x − x j ) } \{\phi(x-x_j)\} {ϕ(x−xj)} 就是线性无关的,从而形成径向基函数空间中某子空间的一组基。当 { x j } \{x_j\} {xj} 几乎充满 R R R 时, { x j } \{x_j\} {xj} 几乎充满 R R R 时, { ϕ ( x − x j ) } \{\phi(x-x_j)\} {ϕ(x−xj)} 及其线性组合可以逼近几乎任何函数。
各类文献中常用的径向基函数有:
- Kriging 方法的 Gauss 分布函数: ϕ ( r ) = e − c 2 r 2 \phi(r)=e^{-c^2r^2} ϕ(r)=e−c2r2
- Kriging 方法的 Markoff 分布函数: ϕ ( r ) = e − c ∣ r ∣ \phi(r)=e^{-c|r|} ϕ(r)=e−c∣r∣,及其他概率分布函数;
- Hardy 的 Multi-Quadric 函数: ϕ ( r ) = ( c 2 + r 2 ) β \phi(r)=(c^2+r^2)^\beta ϕ(r)=(c2+r2)β(其中 β \beta β 是正的实数);
- Hardy 的逆 Multi-Quadric 函数: ϕ ( r ) = ( c 2 + r 2 ) − β \phi(r)=(c^2+r^2)^{-\beta} ϕ(r)=(c2+r2)−β(其中 β \beta β 是正的实数);
- Duchon 的薄板样条: d d d 为偶数时, ϕ ( r ) = r 2 k − d log r \phi(r)=r^{2k-d}\log r ϕ(r)=r2k−dlogr; d d d 为奇数时, ϕ ( r ) = r 2 k − d \phi(r)=r^{2k-d} ϕ(r)=r2k−d;
二、径向基函数插值
定义:径向基函数插值是对于给定的多元散乱数据 { x j , f j } j = 1 n , x j ∈ R n , f j ∈ R , j = 1 , ⋯ , n \{x_j,f_j\}^n_{j=1},x_j\in R^n,f_j\in R,j=1,\cdots,n {xj,fj}j=1n,xj∈Rn,fj∈R,j=1,⋯,n。选取径向函数 ϕ : R + → R \phi:R_+\rightarrow R ϕ:R+→R 来构造函数系 { ϕ ( ∣ ∣ x − x j ∣ ∣ ) } j = 1 n \{\phi(||x-x_j||)\}_{j=1}^n {ϕ(∣∣x−xj∣∣)}j=1n 并寻找形如 S ( x ) = ∑ j = 1 n λ j ϕ ( ∣ ∣ x − x j ∣ ∣ ) S(x)=\sum_{j=1}^n\lambda_j\phi(||x-x_j||) S(x)=∑j=1nλjϕ(∣∣x−xj∣∣) 的插值函数 S ( x ) S(x) S(x),使其满足条件 S ( x j ) = f j , j = 1 , ⋯ , n S(x_j)=f_j,j=1,\cdots,n S(xj)=fj,j=1,⋯,n。
为了方便,我们定义
{ f T = ( f 1 , f 2 , ⋯ , f n ) ϕ T ( x ) = ( ϕ ( ∣ ∣ x − x 1 ∣ ∣ , ϕ ( ∣ ∣ x − x 2 ∣ ∣ , ⋯ , ϕ ( ∣ ∣ x − x n ∣ ∣ ) ) λ T = ( λ 1 , λ 2 , ⋯ , λ n ) A = ( ϕ ( ∣ ∣ x j − x k ∣ ∣ ) ) n × n \begin{cases} \pmb{f^T}=(f_1,f_2,\cdots,f_n)\\[2ex] \pmb{\phi^T}(x)=\Big(\phi(||x-x_1||,\phi(||x-x_2||,\cdots,\phi(||x-x_n||)\Big)\\[2ex] \pmb{\lambda^T}=(\lambda_1,\lambda_2,\cdots,\lambda_n)\\[2ex] \pmb{A}=\Big(\phi(||x_j-x_k||)\Big)_{n\times n} \end{cases} ⎩ ⎨ ⎧fT=(f1,f2,⋯,fn)ϕT(x)=(ϕ(∣∣x−x1∣∣,ϕ(∣∣x−x2∣∣,⋯,ϕ(∣∣x−xn∣∣))λT=(λ1,λ2,⋯,λn)A=(ϕ(∣∣xj−xk∣∣))n×n
上述插值方程对任意两两不同的 x j x_j xj 的数据 { x j , f j } \{x_j,f_j\} {xj,fj} 有解的充要条件是:对任意两两不同的 x j x_j xj,对称矩阵 A \pmb A A 都非奇异。
定理:函数 ϕ : R + → R \phi:R_+\rightarrow R ϕ:R+→R 是连续的, lim r → ∞ ϕ ( r ) = 0 \lim_{r\rightarrow\infty}\phi(r)=0 limr→∞ϕ(r)=0,那么对于 n n n 元的径向基函数插值总是存在唯一解的充分条件是:矩阵 A \pmb A A 是正定矩阵。
上面提到的径向基函数中逆 Multi-Quadric 函数和 Gauss 函数在任意维空间上都是正定函数,因此插值是唯一的。
三、用高斯函数进行散乱数据的插值
对于数据量少的情况,径向基函数(尤其是高斯函数)插值的结果较令人满意,而且计算也比较简单。
令径向基函数插值方程为
S ( x ) = ∑ j = 1 n λ j ϕ ( ∣ ∣ x − x j ∣ ∣ ) S(x)=\sum_{j=1}^n\lambda_j\phi(||x-x_j||) S(x)=j=1∑nλjϕ(∣∣x−xj∣∣)
将已知点 ( x j , f j ) , j = 1 , ⋯ , n (x_j,f_j),j=1,\cdots,n (xj,fj),j=1,⋯,n 代入方程,可得:
[ λ 1 λ 2 ⋯ λ n ] [ ϕ ( ∣ ∣ x 1 − x 1 ∣ ∣ ) ϕ ( ∣ ∣ x 2 − x 1 ∣ ∣ ) ⋯ ϕ ( ∣ ∣ x n − x 1 ∣ ∣ ) ϕ ( ∣ ∣ x 1 − x 2 ∣ ∣ ) ϕ ( ∣ ∣ x 2 − x 2 ∣ ∣ ) ⋯ ϕ ( ∣ ∣ x n − x 2 ∣ ∣ ) ⋮ ⋮ ⋮ ϕ ( ∣ ∣ x 1 − x n ∣ ∣ ) ϕ ( ∣ ∣ x 2 − x n ∣ ∣ ) ⋯ ϕ ( ∣ ∣ x n − x n ∣ ∣ ) ] = [ f 1 f 2 ⋯ f n ] \left[ \begin{matrix} \lambda_1 & \lambda_2 & \cdots & \lambda_n\\ \end{matrix} \right] \left[ \begin{matrix} \phi(||x_1-x_1||) & \phi(||x_2-x_1||) & \cdots & \phi(||x_n-x_1||)\\ \phi(||x_1-x_2||) & \phi(||x_2-x_2||) & \cdots & \phi(||x_n-x_2||)\\ \vdots & \vdots & & \vdots\\ \phi(||x_1-x_n||) & \phi(||x_2-x_n||) & \cdots & \phi(||x_n-x_n||)\\ \end{matrix} \right]= \left[ \begin{matrix} f_1& f_2& \cdots& f_n\\ \end{matrix} \right] [λ1λ2⋯λn] ϕ(∣∣x1−x1∣∣)ϕ(∣∣x1−x2∣∣)⋮ϕ(∣∣x1−xn∣∣)ϕ(∣∣x2−x1∣∣)ϕ(∣∣x2−x2∣∣)⋮ϕ(∣∣x2−xn∣∣)⋯⋯⋯ϕ(∣∣xn−x1∣∣)ϕ(∣∣xn−x2∣∣)⋮ϕ(∣∣xn−xn∣∣) =[f1f2⋯fn]
求解上述方程,可求出 λ 1 , λ 2 , ⋯ , λ n \lambda_1,\lambda_2,\cdots,\lambda_n λ1,λ2,⋯,λn 的值,从而求出插值曲线方程。插值曲面方程类似,将 x x x 替换成向量 X X X 即可。
具体应用到高斯函数,设高斯函数插值方程为
S ( x ) = ∑ j = 1 n λ j e − α ∣ ∣ x − x j ∣ ∣ 2 α > 0 S(x)=\sum_{j=1}^n\lambda_je^{-\alpha||x-x_j||^2}\quad\alpha>0 S(x)=j=1∑nλje−α∣∣x−xj∣∣2α>0
其中, α \alpha α 为形状调整参数,可根据散乱数据点分布特征选取,当数据点对应的函数值变化较大时, α \alpha α 可取的稍大些;数据点对应的函数值变化较小时, α \alpha α 可取得稍小些。
python 代码实现
import numpy as np
import matplotlib.pyplot as pltdef gen_data(x1, x2):# 用于生成插值节点和总数据点 x1,x2 分别为插值节点的横坐标构成的行向量,总数据点的横坐标构成的行向量y_sample = np.sin(np.pi * x1 / 2) + np.cos(np.pi * x1 / 3) # 插值节点的函数值y_all = np.sin(np.pi * x2 / 2) + np.cos(np.pi * x2 / 3) # 总数据点的函数值return y_sample, y_alldef kernel_interpolation(y_sample, x1, sig):# 求解插值函数中高斯基函数的系数gaussian_kernel = lambda x, c, h: np.exp(-h*(x - x[c]) ** 2) # 高斯基函数num = len(y_sample)w = np.zeros(num)int_matrix = np.asmatrix(np.zeros((num, num)))for i in range(num):int_matrix[i, :] = gaussian_kernel(x1, i, sig)w = np.asmatrix(y_sample) * int_matrix.Iw = w.Treturn wdef kernel_interpolation_rec(w, x1, x2, sig):gkernel = lambda x, xc, h: np.exp(-h*(x - xc) ** 2) # 高斯基函数num = len(x2)y_rec = np.zeros(num)for i in range(num):for k in range(len(w)):y_rec[i] = y_rec[i] + w[k] * gkernel(x2[i], x1[k], sig)return y_recif __name__ == '__main__':snum = 20 # control point数量ratio = 20 # 总数据点数量:snum*ratiosig = 0.5 # 核函数宽度xs = -8xe = 8x1 = np.linspace(xs, xe, snum)x2 = np.linspace(xs, xe, (snum - 1) * ratio + 1)y_sample, y_all = gen_data(x1, x2)plt.figure(1)w = kernel_interpolation(y_sample, x1, sig)y_rec = kernel_interpolation_rec(w, x1, x2, sig)plt.plot(x2, y_rec, 'k')plt.plot(x2, y_all, 'r:')plt.ylabel('y')plt.xlabel('x')for i in range(len(x1)):plt.plot(x1[i], y_sample[i], 'go', markerfacecolor='none')plt.legend(labels=['reconstruction', 'original', 'control point'], loc='lower left')plt.title('kernel interpolation:$y=sin(\pi x/2)+cos(\pi x/3)$')plt.show()运行结果
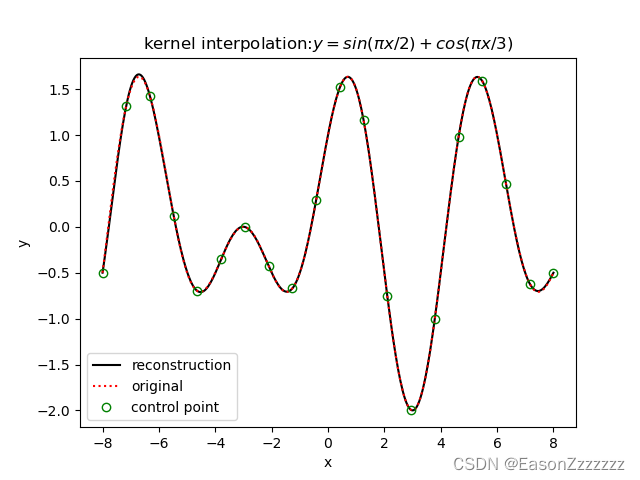
Matlab 代码实现
clc;clear;%% 参数
snum = 20; % 插值节点个数
ratio = 20; % 总数据点个数:(snum-1)*ratio + 1
sig = 0.5; % 形状控制参数xs = -8; % 起点
xe = 8; % 终点%% 生成样本点
x1 = linspace(xs,xe,snum); % 生成插值点坐标
x2 = linspace(xs,xe,(snum-1)*ratio + 1);
[y_sample,y_all] = gen_data(x1,x2);figure('Name','RBF插值方法')%% 计算基函数技术lambda
w = kernel_interpolation(y_sample,x1,sig);%% 重构曲线
y_rec = kernel_interpolation_rec(w,x1,x2,sig);%% 绘图
plot(x2,y_rec,'--',x2,y_all,':','LineWidth',2)
hold on
for i = 1:1:length(x1)scatter(x1(i),y_sample(i),70,'green')
endtitle('$y=sin(\pi x/2)+cos(\pi x/3)$','Interpreter','latex')
xlabel('x')
ylabel('y')
legend('重构曲线','原始曲线','插值点','Location','southwest')%% 生成插值节点和总数据点
function [y_sample,y_all] = gen_data(x1,x2)
y_sample = sin(pi * x1 / 2) + cos(pi * x1 / 3);
y_all = sin(pi * x2 / 2) + cos(pi * x2 / 3);
end%% 求解插值函数中高斯基函数的系数
function w = kernel_interpolation(y_sample,x1,sig)
num = length(y_sample);
int_matrix = zeros(num,num);for i = 1:1:num int_matrix(i,:) = exp(-sig.*(x1-x1(i)).^2);
endw = y_sample * inv(int_matrix);
end%% 重构曲线
function y_rec = kernel_interpolation_rec(w,x1,x2,sig)
num = length(x2);
y_rec = zeros(1,num);for i = 1:1:numfor k = 1:1:length(w)y_rec(i) = y_rec(i) + w(k) .* exp(-sig.*(x2(i)-x1(k)).^2);end
end
end运行结果
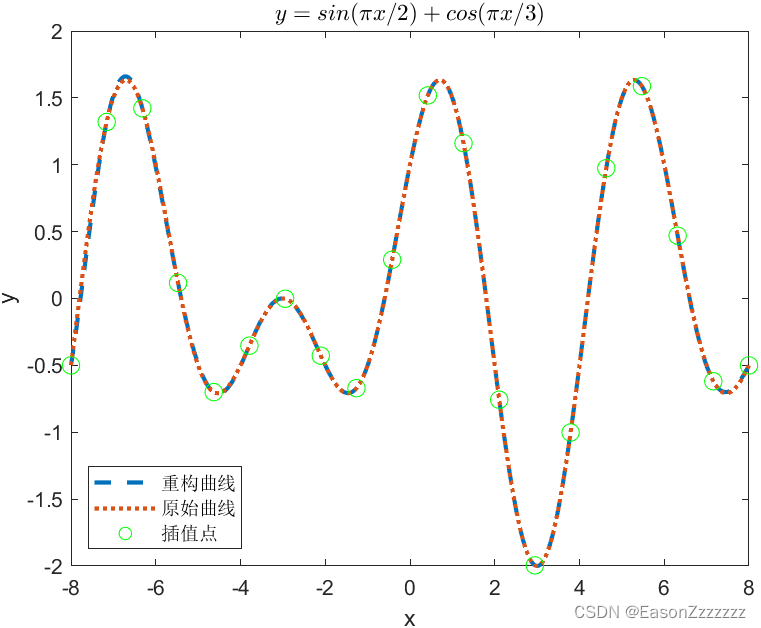




:绘图)




)




】堆内存申请(排序和贪心算法-JavaPythonC++JS实现))




