【leetcode】力扣算法之相交链表【中等难度】

题目描述

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

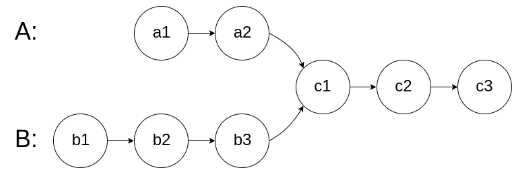
图示两个链表在节点 c1 开始相交：
在这里插入图片描述
题目数据保证整个链式结构中不存在环。

注意，函数返回结果后，链表必须保持其原始结构。

自定义评测：

评测系统的输入如下（你设计的程序不适用此输入）：

intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0
listA - 第一个链表
listB - 第二个链表
skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数
skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数
评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被视作正确答案。

用例

输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at ‘8’
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
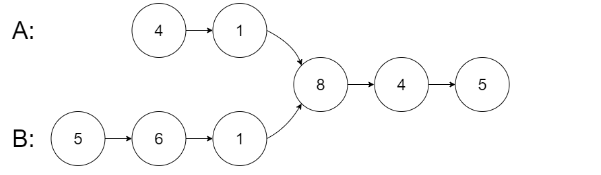
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。
— 请注意相交节点的值不为 1，因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说，它们在内存中指向两个不同的位置，而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点，B 中第四个节点) 在内存中指向相同的位置。
在这里插入图片描述

输入：intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Intersected at ‘2’
解释：相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。
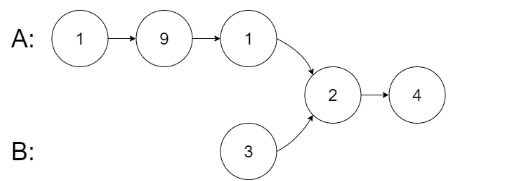
从各自的表头开始算起，链表 A 为 [1,9,1,2,4]，链表 B 为 [3,2,4]。
在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

在这里插入图片描述

输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：null
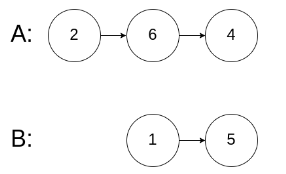
解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。
由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
这两个链表不相交，因此返回 null 。

在这里插入图片描述

提示：

listA 中节点数目为 m
listB 中节点数目为 n
1 <= m, n <= 3 * 104
1 <= Node.val <= 105
0 <= skipA <= m
0 <= skipB <= n
如果 listA 和 listB 没有交点，intersectVal 为 0
如果 listA 和 listB 有交点，intersectVal == listA[skipA] == listB[skipB]

示例代码

解法1：暴力破解
解法2：借助数组反向查找

var getIntersectionNode = function(headA, headB) {let temp=[];while(headA){temp.push(headA);if(headA.next){headA=headA.next;}else{break;}}let temp1=[];while(headB){temp1.push(headB);if(headB.next){headB=headB.next;}else{break;}}let res=null;let min=Math.min(temp.length,temp1.length);for(let i=0;i<min;i++){if(temp[temp.length-1-i]==temp1[temp1.length-1-i]){res=temp[temp.length-1-i];}else{break;}}return res;
};

在这里插入图片描述

解法3：奇怪的解法

var getIntersectionNode = function(headA, headB) {if(!headA || !headB) return null;let pA=Object.assign(headA);let pB=Object.assign(headB);while(pA!=pB){pA = pA == null ? headB : pA.next;pB = pB == null ? headA : pB.next;}return pA;
};