假设你有一组 3D 中的 n 个点，并且想要为它们拟合一个平面。 在本文中，我将推导出一个简单的、数值稳定的方法，并提供它的源代码。 听起来很好玩？ 我们开始吧！

NSDT工具推荐： Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎

首先，如果在网上寻找答案，你将得到的答案包括对协方差矩阵进行奇异值分解以找到最小特征值的特征向量。 然而事实证明，这让事情变得比他们需要的更加复杂。 让我们从基础开始：

平面通常由法向量 n = [a, b, c]ᵀ 和距离 d 描述，因此对于平面 n · p + d = 0 上的点 p = [x, y, z]ᵀ。我们可以 将其写为：

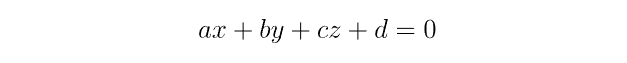
但请注意，这是超定的 - 解空间（平面）是三维的，但上面的描述使用了四个值。 因此，让我们首先通过限制解决方案空间来删除一个组件。 我们通过任意指定 c = 1 来实现这一点，即平面法线的 z 分量始终为 1（请注意，法线的长度不需要为 1）。 如果你认为这是一个潜在有问题的假设，那么你是对的——我们稍后会再讨论这个问题。 现在，让我们定义：

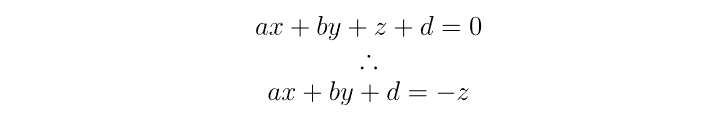
并求解a、b、d。 矩阵形式：

接下来，我们将这个矩阵转置，然后从左侧相乘以执行线性最小二乘：

转置后相乘：

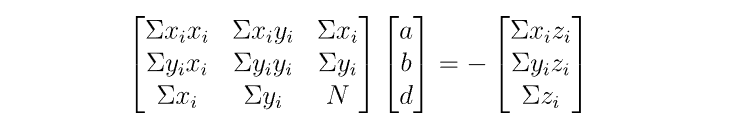
其中 N 是点数。 现在这是聪明的部分：让我们定义上面的 x,y,z 相对于点云的质心（平均值）。 现在 Σx = Σy = Σz = 0 所以我们可以简化为：

从最后一行（N·d = 0）我们可以得出结论：d = 0。这意味着如果所有点都相对于点云的质心，则平面穿过原点。 换句话说：平面始终穿过输入点的平均值。 我们现在可以去掉一个维度：

克莱默规则告诉我们：

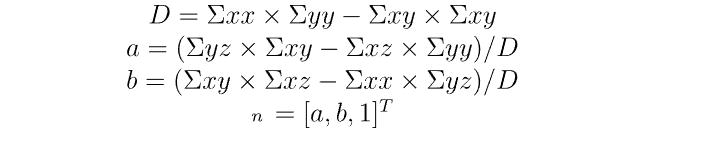
我们可以通过将 n 乘以 D 来简化它（无论如何我们都需要对 n 进行归一化），这给我们：

就是这样！ 但请记住我们的假设：平面法线的 z 分量不为零。 如果为零怎么办？ 那么可以证明上面的行列式 D 变为零并且我们可以除以零。 即使它不完全为零，但很接近，我们仍然会得到不好的条件，从而得到不好的结果。 所以，我们能做些什么？ 好吧，如果这些点跨越一个平面，则法线的至少一个分量必须非零。 因此，让我们对三个单独的假设进行上述计算，其中哪个分量不为零。 然后我们简单地选择表现最好的一个，即具有最大行列式的那个。

注意：此方法将最小化垂直于主轴的残差的平方，而不是垂直于平面的残差的平方。 如果残差很小（即你的点都靠近生成的平面），那么这种方法可能就足够了。 但是，如果你的点分布比较分散，那么此方法可能不是最合适的。

这是 Rust 代码：

// Constructs a plane from a collection of points
// so that the summed squared distance to all points is minimzized
fn plane_from_points(points: &[Vec3]) -> Option<Plane> {if points.len() < 3 {return None; // At least three points required}let mut sum = Vec3{x:0.0, y:0.0, z:0.0};for p in points {sum += p;}let centroid = sum * (1.0 / (points.len() as f64));// Calc full 3x3 covariance matrix, excluding symmetries:let mut xx = 0.0; let mut xy = 0.0; let mut xz = 0.0;let mut yy = 0.0; let mut yz = 0.0; let mut zz = 0.0;for p in points {let r = p - centroid;xx += r.x * r.x;xy += r.x * r.y;xz += r.x * r.z;yy += r.y * r.y;yz += r.y * r.z;zz += r.z * r.z;}let det_x = yy*zz - yz*yz;let det_y = xx*zz - xz*xz;let det_z = xx*yy - xy*xy;let det_max = max3(det_x, det_y, det_z);if det_max <= 0.0 {return None; // The points don't span a plane}// Pick path with best conditioning:let dir =if det_max == det_x {Vec3{x: det_x,y: xz*yz - xy*zz,z: xy*yz - xz*yy,}} else if det_max == det_y {Vec3{x: xz*yz - xy*zz,y: det_y,z: xy*xz - yz*xx,}} else {Vec3{x: xy*yz - xz*yy,y: xy*xz - yz*xx,z: det_z,}};Some(plane_from_point_and_normal(centroid, normalize(dir)))
}

---

原文链接：3D点云平面拟合 - BimAnt