目录
- 归并排序
- 概念
- 算法思想
- 第一步
- 第二步
- 第三步
- 算法步骤
- 代码实现
- 代码1
- 代码优化
- 时间复杂度
- 空间复杂度
- 特性总结
归并排序
概念
归并排序(Merge Sort)是一种基于分治策略的经典排序算法。它的基本思想是将待排序的数组划分成两个子数组,分别对这两个子数组进行递归排序,然后将已排序的子数组合并成一个有序的数组。归并排序的关键在于合并操作,这是该算法的核心。
算法思想
归并、归并,其实可以认为就是递归+合并。递归就是将待排序的数组通过递归,细分到子数组有序为止。最差的情况,如细分到数组只剩一个元素,那么该数组既可以认为是升序的,也可以认为是降序的,总而言之,是有序的。
然后将一个个有序的数组,进行合并,最终合并成一个有序的数组。因此该排序算法的核心便是合并算法。
我们借助数组arr = { 6 , 4 , 3 , 2 , 5 , 8 , 1 , 7 }。借用图形模拟演示下流程。
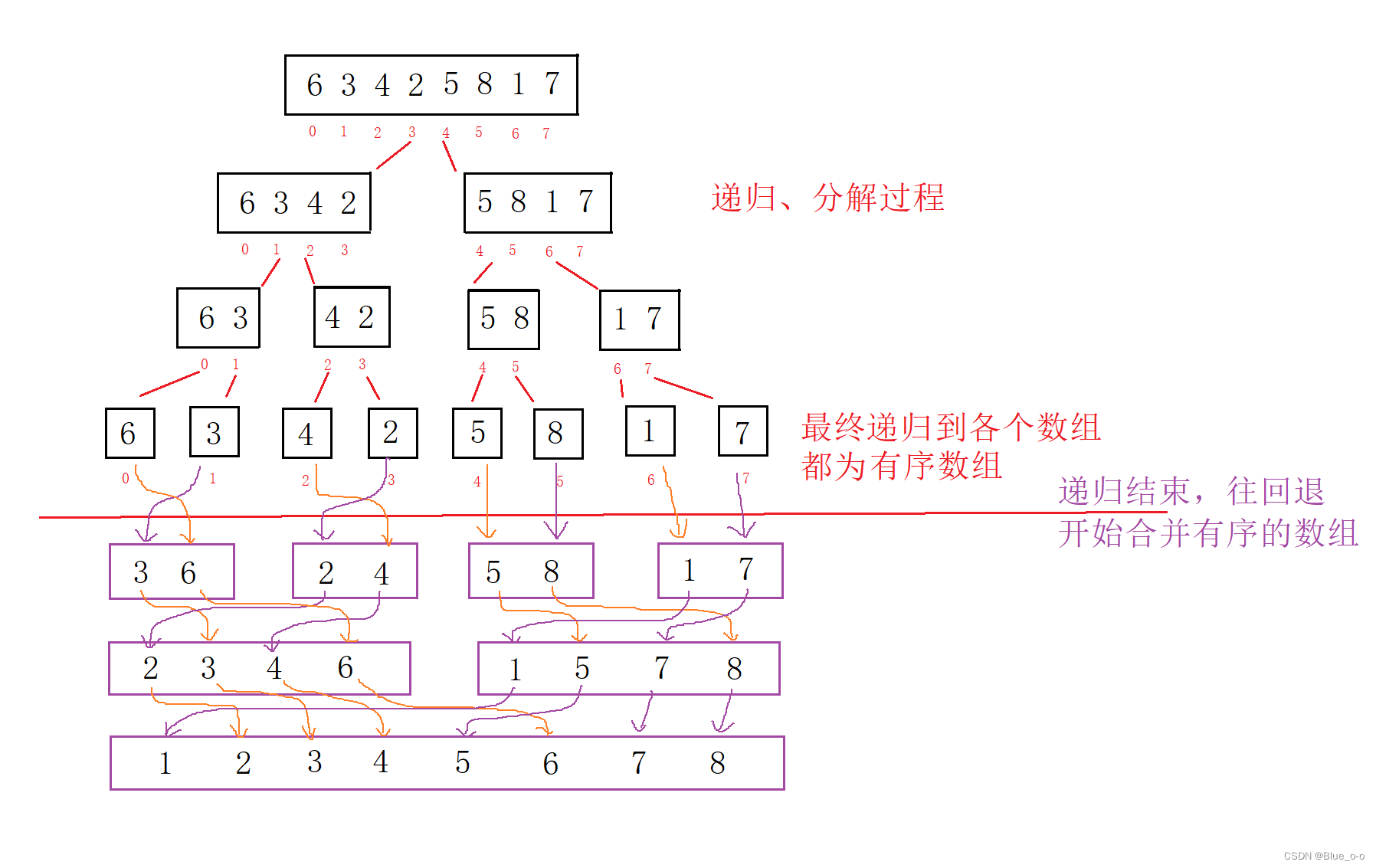
通过上图所示的流程图,或许看着比较通俗易懂,然后实际上用代码实现起来还是没有想象中的那么简单的。
第一步
首先,我们不可能如流程图演示一样,递归一次就开辟一些新的数组,而且频繁的开辟数组也会造成性能的浪费。因此,在一开始便会申请一块与待排序数组同样空间大小的临时数组tmp。
// 归并排序 - 递归实现
void MergeSort(int* a, int n)
{assert(a); // 确保数组不为空int* tmp = (int*)malloc(sizeof(int) * n);free(tmp); // 申请的空间,没用时要主动释放
}
解决了临时空间的问题,下一步我们将着手解决递归和合并的问题。
第二步
因为待排序的数据与后序递归细分到有序数组都是一样的问题,我们可以统一给它们划分成一个子问题,如以下的_MergeSort()函数:
// 归并排序 - 递归实现
void MergeSort(int* a, int n)
{assert(a);int* tmp = (int*)malloc(sizeof(int) * n);_MergeSort(a, 0, n - 1, tmp); // 子问题,解决递归和合并的问题free(tmp);}
因为递归划分数组时,是根据数组下标进行划分的,因此子函数设计时,传入数组下标的范围更佳,同时要将临时数组tmp也传过去。
第三步
如下,对数组进行划分,分别用left 和 right 接收传入的数组下标的范围,然后通过下标算出数组的中间下标值,用 变量mid接收,根据变量mid,将数组划分为两个区间,区间范围为:[ left , mid ] 、 [ mid+1 , right ] 。
而对于[ left , mid ] 和 [ mid+1 , right ] 两个子数组若是有序,则可以进行合并;如果还没有序时,依旧是子问题,这便是递归的由来。
子函数_MergeSort(),传入的参数依旧是待排序数组的下标范围,和临时辅助的数组tmp。如下代码所示:
// 时间复杂度:O(N*logN)
// 空间复杂度:O(N)
void _MergeSort(int* a, int left, int right, int* tmp)
{int mid = (left + right) / 2;// 分割为两个区间[left,mid] [mid+1,right]//[left,mid] [mid+1,right] 有序,则可以合并,他们还没有序时,子问题解决_MergeSort(a, left, mid, tmp);_MergeSort(a, mid + 1, right, tmp);
}观察以上的代码,我们发现,
1、递归函数中,缺少了结束条件,这将导致一直递归个不停,从而导致栈溢出,致使程序崩溃。而如何确定结束条件呢?回顾流程图,当数组中只有一个元素时,便可以认为数组是有序的了,即当待排序数组的下标范围, left >= right 时便可以结束递归,返回,进行合并了。
2、缺少合并的步骤。
因此,要解决以上两个问题,如下:
// 时间复杂度:O(N*logN)
// 空间复杂度:O(N)
void _MergeSort(int* a, int left, int right, int* tmp)
{if (left >= right)return;int mid = (left + right) / 2;// 分割为两个区间[left,mid] [mid+1,right]//[left,mid] [mid+1,right] 有序,则可以合并,他们还没有序时,子问题解决_MergeSort(a, left, mid, tmp);_MergeSort(a, mid + 1, right, tmp);/* 当执行到这里时,数组[left,mid] 和 [mid+1 , right] 已经有序,因此下面将是退出递归、合并数组的步骤 */// 归并:递归往回退 ([left,mid]、[mid+1,right]两个区间已经有序)int begin1 = left, end1 = mid;int begin2 = mid+1, end2 = right;int index = begin1; // 此处注意,tmp起始位置在 leftwhile (begin1 <= end1 && begin2 <= end2){// 在两个数组中,依次找最小的数存入临时数组tmpif (a[begin1] < a[begin2])tmp[index++] = a[begin1++];elsetmp[index++] = a[begin2++];}// 一组数组归并完,将另一组数组剩下的全部归并到后面,结束的那一组将不会进入while循环while (begin1 <= end1)tmp[index++] = a[begin1++];while (begin2 <= end2)tmp[index++] = a[begin2++];// 把归并好的在tmp的数据,再拷贝回到原数组for (int i = left; i <= right; i++)a[i] = tmp[i];}
以上,需要注意的是:
1、当待排序的数组还未有序时,统一归纳为子问题,继续递归下去。直到待排序数组有序时(数组只有一个元素)才开始递归返回,接着执行数组的合并。
2、需要将待合并的两个数组,挨个选取两个数组中最小(升序)/最大(降序)的数放入临时数组tmp中。同时需要注意,临时数组tmp的下标问题。
3、将两个待合并的数组,有序的合并到临时数组tmp,返回上一级递归前,需要将临时数组中合并好的、排好序数组,拷贝回原数组。
以上便是对于归并算法的大体流程,下面是对于该算法的步骤大体总结。
算法步骤
1、分割数组: 将待排序的数组划分为两个相等(或近似相等)大小的子数组。这一步采用分治策略,递归地对子数组进行分割,直到每个子数组包含一个元素。
2、递归排序: 对分割后的子数组进行递归排序。这是通过再次调用归并排序来实现的。
3、合并操作: 将已排序的子数组合并成一个有序数组。合并操作是归并排序的关键步骤,它涉及比较已排序的子数组的元素,并按顺序将它们合并到一个新的数组中。
结合以上的全部学习,让我们给出完整的代码,进行学习上的整合。
代码实现
代码1
// 时间复杂度:O(N*logN)
// 空间复杂度:O(N)
void _MergeSort(int* a, int left, int right, int* tmp)
{if (left >= right)return;int mid = (left + right) / 2;// 分割为两个区间[left,mid] [mid+1,right]//[left,mid] [mid+1,right] 有序,则可以合并,他们还没有序时,子问题解决_MergeSort(a, left, mid, tmp);_MergeSort(a, mid + 1, right, tmp);/* 分解 + 合并 */// 归并:递归往回退 ([left,mid]、[mid+1,right]两个区间已经有序)int begin1 = left, end1 = mid;int begin2 = mid+1, end2 = right;int index = begin1; // 此处注意,tmp起始位置在 leftwhile (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2])tmp[index++] = a[begin1++];elsetmp[index++] = a[begin2++];}// 一组数组归并完,将另一组数组剩下的全部归并到后面,结束的那一组将不会进入while循环while (begin1 <= end1)tmp[index++] = a[begin1++];while (begin2 <= end2)tmp[index++] = a[begin2++];// 把归并好的在tmp的数据,再拷贝回到原数组for (int i = left; i <= right; i++)a[i] = tmp[i];}// 归并排序 - 递归实现
void MergeSort(int* a, int n)
{assert(a);int* tmp = (int*)malloc(sizeof(int) * n);_MergeSort(a, 0, n - 1, tmp);free(tmp);}
以上便是对于归并算法的具体代码实现。其中,为了更好的函数封装性。我们可以将具体的合并过程,封装成一个合并函数,使代码可读性更强。如下:
代码优化
// 合并处理函数
void MergeArr(int* a, int begin1, int end1, int begin2, int end2, int* tmp)
{int left = begin1, right = end2;int index = begin1; // 此处注意,tmp起始位置在 leftwhile (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2])tmp[index++] = a[begin1++];elsetmp[index++] = a[begin2++];}// 一组数组归并完,将另一组数组剩下的全部归并到后面,结束的那一组将不会进入while循环while (begin1 <= end1)tmp[index++] = a[begin1++];while (begin2 <= end2)tmp[index++] = a[begin2++];// 把归并好的在tmp的数据,再拷贝回到原数组for (int i = left; i <= right; i++)a[i] = tmp[i];
}// 时间复杂度:O(N*logN)
// 空间复杂度:O(N)
void _MergeSort(int* a, int left, int right, int* tmp)
{if (left >= right)return;int mid = (left + right) / 2;// 分割为两个区间[left,mid] [mid+1,right]//[left,mid] [mid+1,right] 有序,则可以合并,他们还没有序时,子问题解决_MergeSort(a, left, mid, tmp);_MergeSort(a, mid + 1, right, tmp);/* 分解 + 合并 */// 归并:递归往回退 ([left,mid]、[mid+1,right]两个区间已经有序)MergeArr(a, left, mid, mid + 1, right, tmp);}// 归并排序 - 递归实现
void MergeSort(int* a, int n)
{assert(a);int* tmp = (int*)malloc(sizeof(int) * n);_MergeSort(a, 0, n - 1, tmp);free(tmp);}以上便是封装性更佳的归并算法。
时间复杂度
O(N*logN)
归并排序有点类似于二叉树中的后序遍历。先将数组平分、平分,直到最后不能再分时,再合并返回。
因为递归的高度为logN,而合并的过过程,每一层可以归纳统计认为是N。
因此归并排序的时间复杂度为:O(N*logN)。
空间复杂度
O(N)
该算法需要用到额外开辟的数组。数组大小为待排序数组的大小。故空间复杂度为O(N)。
(N为待排序数组的个数)
特性总结
1、 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问
题。
2、时间复杂度:O(N*logN)
3、空间复杂度:O(N)
4、稳定性:稳定


)
)
这一编译过程中的步骤)





 函数创建 Vnodes)


![[足式机器人]Part2 Dr. CAN学习笔记-动态系统建模与分析 Ch02-7二阶系统](http://pic.xiahunao.cn/[足式机器人]Part2 Dr. CAN学习笔记-动态系统建模与分析 Ch02-7二阶系统)





