与多臂老虎机问题不同,马尔可夫决策过程包含状态信息以及状态之间的转移机制。如果要用强化学习去解决一个实际问题,第一步要做的事情就是把这个实际问题抽象为一个马尔可夫决策过程。
马尔可夫决策过程描述
马尔可夫决策过程以智能体在与环境交互的过程中,学习的过程。智能体:充当做出决策、动作,并在交互过程中学习的角色。环境:智能体与之交互的一切外在事物,不包括智能体本身。
例如弹钢琴,我们本身为作为决策和学习的智能体,与之交互的钢琴是环境。我们通过钢琴发出的声音来判断按的力度是否合理,可以对下次弹的动作进行修正,这就是反馈。
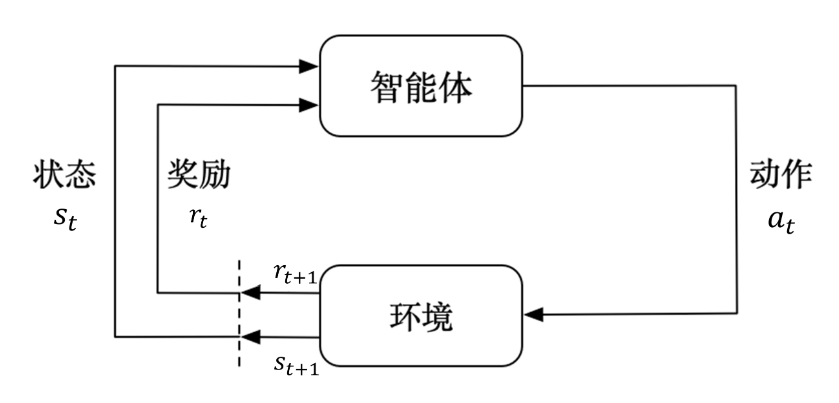
智能体与环境每次交互以时步表示,以t表示时步, t = 0 , 1 , 2.... t=0,1,2.... t=0,1,2....,每一步代表交互一次,而不是现实世界中过一秒。在每个时步t中,智能体可以观测或接收当前环境的状态 s t s_t st ,根据 s t s_t st 执行动作 a t a_t at 。执行动作 a t a_t at 后会得到奖励 r t + 1 r_{t+1} rt+1 ,同时环境会因为动作 a t a_t at 的影响进行改变,成为新的状态 s t + 1 s_{t+1} st+1 ,在下一时步被观测到,并进行循环。,即:
s 0 , a 0 , r 1 , s 1 , a 1 , r 2 , . . . , s t , a t , r t + 1 s_0,a_0,r_1,s_1,a_1,r_2,...,s_t,a_t,r_{t+1} s0,a0,r1,s1,a1,r2,...,st,at,rt+1
奖励可能是正的,也可能是负的,如同上课被老师表扬或批评。
马尔可夫性质
马尔可夫性质如下式所示:
P ( s t + 1 ∣ s t ) = P ( S t + 1 ∣ s 0 , s 1 , . . . , s t ) P(s_{t+1}|s_t)=P(S_{t+1}|s_0,s_1,...,s_t) P(st+1∣st)=P(St+1∣s0,s1,...,st)
即在 s t s_t st 发生的情况下 s t + 1 s_{t+1} st+1 发生的概率与 s 0 , s 1 , . . . , s t s_0,s_1,...,s_t s0,s1,...,st 都发生(或已知)的情况下相同,因此可以理解为,未来的状态只与当前的状态 s t s_t st 有关,不受过去状态的影响,允许我们在没有考虑系统完整的历史下进行预测和控制。但棋类游戏等需要了解历史走子情况,可以在后续的学习中靠决策模型、深度学习等解决。
但我们要注意,具有马尔可夫性不代表与历史完全没有关系,虽然 t + 1 t+1 t+1 时刻的状态只与 t t t 时刻的状态有关系,但是 t t t 时刻包含了 t − 1 t-1 t−1 时刻的状态与信息。马尔可夫性简化了运算,只需要知道当前状态(已经包含了历史信息),不需要将以前的历史信息与状态带入运算了。
状态转移矩阵
在大多数强化学习场景中,状态一般是有限的,我们成为有限状态马尔可夫决策过程(finite MDP)。既然状态数量是有限的,可以通过状态流向图表示智能体与环境交互过程中的走向,可以构建马尔可夫链。
我们举一个例子,假设学生正在上课,一般来讲从老师的角度来说学生会有三种状态,认真听讲、玩手机和睡觉,分别用 s 1 s_1 s1 , s 2 s_2 s2 和 s 3 s_3 s3 表示。
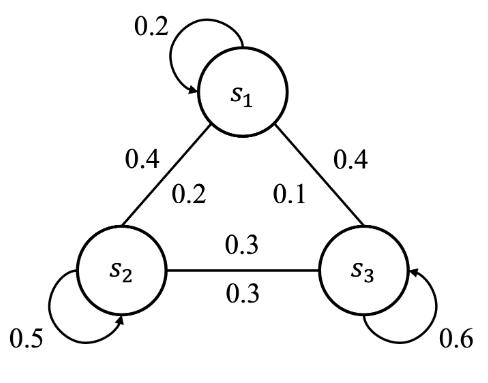
学生认真听课时处于状态 s 1 s_1 s1,会有0.2的概率继续认真听讲,分别有0.4和0.4的概率会去玩手机 s 2 s_2 s2 或者睡觉 s 3 s_3 s3 ,可以表示为
P 12 = P ( S t + 1 = s 2 ∣ S t = s 1 ) = 0.4 P_{12}=P(S_{t+1}=s_2|S_{t}=s_1)=0.4 P12=P(St+1=s2∣St=s1)=0.4
拓展到所有的状态:
P s s ′ = P ( S t + 1 = s ′ ∣ S t = s ) P_{ss'}=P(S_{t+1}=s'|S_t=s) Pss′=P(St+1=s′∣St=s)
即表示当前状态是s,下一个状态是s’的概率
可以列成下表:
| S t + 1 = s 1 S_{t+1}=s_1 St+1=s1 | S t + 1 = s 2 S_{t+1}=s_2 St+1=s2 | S t + 1 = s 3 S_{t+1}=s_3 St+1=s3 | |
|---|---|---|---|
| S t = s 1 S_t=s_1 St=s1 | 0.2 | 0.4 | 0.4 |
| S t = s 2 S_t=s_2 St=s2 | 0.2 | 0.5 | 0.3 |
| S t = s 3 S_t=s_3 St=s3 | 0.1 | 0.3 | 0.6 |
在数学上也可以使用矩阵来表示:
P s s ′ = [ 0.2 0.4 0.4 0.2 0.5 0.3 0.1 0.3 0.6 ] P_{ss'}=\begin{bmatrix} 0.2 & 0.4 & 0.4\\ 0.2 & 0.5 & 0.3\\ 0.1 & 0.3 & 0.6 \\ \end{bmatrix} Pss′= 0.20.20.10.40.50.30.40.30.6
通用的表示方法为:
P s s ′ = ( p 11 p 12 ⋯ p 1 n p 21 p 22 ⋯ p 2 n ⋮ ⋮ ⋱ ⋮ p n 1 p n 2 ⋯ p n n ) P_{ss^{\prime}}=\begin{pmatrix}p_{11}&p_{12}&\cdots&p_{1n}\\p_{21}&p_{22}&\cdots&p_{2n}\\\vdots&\vdots&\ddots&\vdots\\p_{n1}&p_{n2}&\cdots&p_{nn}\end{pmatrix} Pss′= p11p21⋮pn1p12p22⋮pn2⋯⋯⋱⋯p1np2n⋮pnn
其中, p 12 = P ( s 2 ∣ s 1 ) p_{12}=P(s_2|s_1) p12=P(s2∣s1),即在状态 s 1 s_1 s1 的情况下,转化为状态 s 2 s_2 s2 的概率。
这个矩阵就叫做状态转移矩阵(State Transition Matrix),某一状态的所有状态转移概率之和是1,状态转移矩阵是环境的一部分,与智能体无关。以刚刚的例子描述,老师无法决定学生的状态,只能根据学生的状态做决策,如学生玩手机,老师可以提醒他,让他认真听讲。
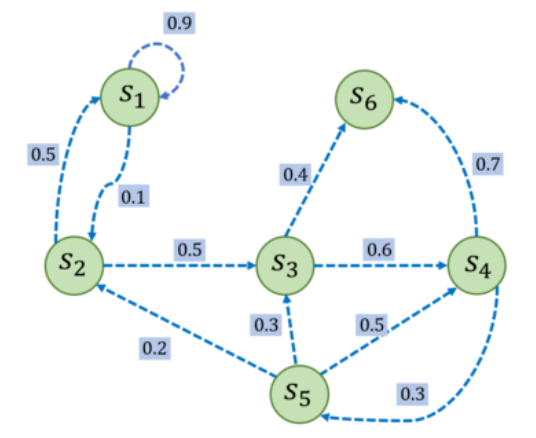
举一个小例子,大家试试手,写下他的状态转移矩阵吧!
P = [ 0.9 0.1 0 0 0 0 0.5 0 0.5 0 0 0 0 0 0 0.6 0 0.4 0 0 0 0 0.3 0.7 0 0.2 0.3 0.5 0 0 0 0 0 0 0 1 ] \mathcal{P}=\begin{bmatrix}0.9&0.1&0&0&0&0\\0.5&0&0.5&0&0&0\\0&0&0&0.6&0&0.4\\0&0&0&0&0.3&0.7\\0&0.2&0.3&0.5&0&0\\0&0&0&0&0&1\end{bmatrix} P= 0.90.500000.10000.2000.5000.30000.600.500000.300000.40.701
s 6 s_6 s6 不转移到其它状态,我们称其为终止状态。给定一个马尔可夫过程,我们就可以从某个状态出发,根据它的状态转移矩阵生成一个状态序列(episode),这个步骤也被叫做采样(sampling)。例如,从 s 1 s_1 s1 出发,可以生成序列 s 1 → s 2 → s 3 → s 6 s_1\to s_2\to s_3 \to s_6 s1→s2→s3→s6
回报
在一个马尔可夫奖励过程中,从第t时刻状态 S t S_t St开始,直到终止状态,所有奖励之和为回报return,用 G t G_t Gt 表示,最简单的回报公式如下文所示:
G t = r t + 1 + r t + 2 + . . . + r T G_t =r_{t+1}+r_{t+2}+...+r_T Gt=rt+1+rt+2+...+rT
T为最后一个时步,即最大的步数(也就是完成了T步,第一个动作 a 0 a_0 a0 完成得到的第一个奖励是 r 1 r_1 r1 ,第T个动作,奖励为 r T r_T rT ),这是描述玉有限步骤,如一局游戏。如果为持续性任务,那么 T → ∞ T \to \infty T→∞ 。
接下来我们引入折扣因子的概念(discount factor) γ \gamma γ :
G t = r t + 1 + γ r t + 2 + γ 2 r t + 3 + ⋯ = ∑ k = 0 T = ∞ γ k r t + k + 1 G_t=r_{t+1}+\gamma r_{t+2}+\gamma^2r_{t+3}+\cdots=\sum_{k=0}^{T=\infty}\gamma^kr_{t+k+1} Gt=rt+1+γrt+2+γ2rt+3+⋯=k=0∑T=∞γkrt+k+1
γ \gamma γ 取值范围为0-1,表示对未来奖励的关注程度,越接近1,对所有未来奖励的关注度越高,可以将本时步的回报 G t G_t Gt 与下一个时步 G t + 1 G_{t+1} Gt+1 有关系:
G t = r t + 1 + γ r t + 2 + γ 2 r t + 3 + γ 3 r t + 4 + ⋯ = r t + 1 + γ ( r t + 2 + γ r t + 3 + γ 2 r t + 4 + ⋯ ) = r t + 1 + γ G t + 1 \begin{aligned} G_{t}& = r_{t+1}+\gamma r_{t+2}+\gamma^2r_{t+3}+\gamma^3r_{t+4}+\cdots \\ &=r_{t+1}+\gamma\left(r_{t+2}+\gamma r_{t+3}+\gamma^2r_{t+4}+\cdots\right) \\ &=r_{t+1}+\gamma G_{t+1} \end{aligned} Gt=rt+1+γrt+2+γ2rt+3+γ3rt+4+⋯=rt+1+γ(rt+2+γrt+3+γ2rt+4+⋯)=rt+1+γGt+1
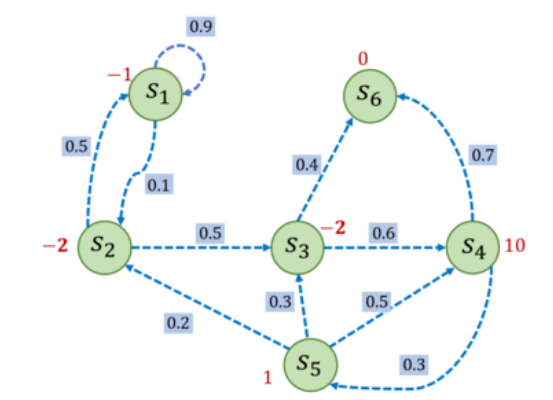
下面举个例子,每个状态旁边的红字为奖励,如果设置折扣因子为0.5,则以序列 s 1 → s 2 → s 3 → s 6 s_1\to s_2\to s_3 \to s_6 s1→s2→s3→s6为例子,设 s 1 s_1 s1 为起始状态,那么 G 1 = − 1 + 0.5 × ( − 2 ) + 0. 5 2 × ( − 2 ) = − 2.5 G_1=-1+0.5×(-2)+0.5^2×(-2)=-2.5 G1=−1+0.5×(−2)+0.52×(−2)=−2.5
import numpy as np
np.random.seed(0)
# 以刚刚的例子定义状态转移概率矩阵
P = [[0.9, 0.1, 0.0, 0.0, 0.0, 0.0],[0.5, 0.0, 0.5, 0.0, 0.0, 0.0],[0.0, 0.0, 0.0, 0.6, 0.0, 0.4],[0.0, 0.0, 0.0, 0.0, 0.3, 0.7],[0.0, 0.2, 0.3, 0.5, 0.0, 0.0],[0.0, 0.0, 0.0, 0.0, 0.0, 1.0],
]
P = np.array(P)
# 定义奖励函数与折扣因子
rewards=[-1,-2,-2,10,1,0]
gamma=0.5
# 给定一个序列,并计算回报
def computeReturn(startIndes,chain,gamma):G=0#按照公式,从后往前计算奖励for i in reversed(range(startIndes,len(chain))):G=gamma*G+rewards[chain[i]-1]ilist.append(i)return G
# 一个状态序列,s1-s2-s3-s6
chain = [1, 2, 3, 6]
startIndes = 0
ilist=[]
G = computeReturn(startIndes, chain, gamma)
print("根据本序列计算得到回报为:%s。" % G)
print(f'i执行的顺序{ilist}')
根据本序列计算得到回报为:-2.5。
i执行的顺序[3, 2, 1, 0]
此外,在马尔可夫链(马尔可夫过程)的基础上增加奖励元素就会形成马尔可夫奖励过程(Markov reward process, MRP)。可以使用五元组描述马尔可夫决策过程 < S , A , R , P , γ > <S,A,R,P,\gamma> <S,A,R,P,γ> ,其中 S 表示状态空间,即所有状态的集合,A 表示动作空间,R 表示奖励函数,P 表示状态转移矩阵, γ \gamma γ 表示折扣因子。

![[嵌入式C][入门篇] 快速掌握基础2 (数据类型、常量、变量)](http://pic.xiahunao.cn/[嵌入式C][入门篇] 快速掌握基础2 (数据类型、常量、变量))
![[NAND Flash 5.3] QLC NAND 已来未热,是时候该拥抱了?](http://pic.xiahunao.cn/[NAND Flash 5.3] QLC NAND 已来未热,是时候该拥抱了?)




技术汇总梳理)
)
:c++ 隐式转换与explicit关键字)



)





