考虑同一个的问题:将由个词元组成的序列映射到另一个长度相同的序列,其中的每个输入词元或输出词元由
维向量表示。
我们将比较能够解决上述问题的三种常用方法:卷积神经网络(CNN)、循环神经网络(RNN)和自注意力(self-attention),从三个维度比较这三种架构:计算复杂度、顺序操作和最大路径长度。
其中,讨论顺序操作是因为顺序操作会妨碍并行计算。任意的序列位置组合之间的路径越短,越能更轻松地学习序列中的远距离依赖关系。
1、卷积神经网络(CNN)
考虑⼀个卷积核⼤⼩为的卷积层。(后续文章中将介绍关于使⽤卷积神经⽹络处理序列的详细信息)⽬前只需要知道的是,由于序列⻓度是
,输⼊和输出的通道数量都是
,所以卷积层的计算复杂度为
。 如图所⽰,卷积神经⽹络是分层的,因此为有
个顺序操作,最⼤路径⻓度为
。例如,
和
处于图中卷积核⼤⼩为3的双层卷积神经⽹络的感受野内。

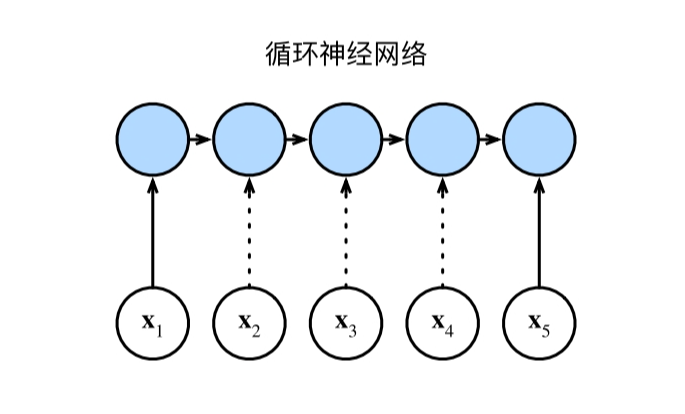
2、循环神经网络(RNN)
当更新循环神经⽹络的隐状态时,权重矩阵和
维隐状态的乘法计算复杂度为
。由于序列⻓度为
, 因此循环神经⽹络层的计算复杂度为
。根据图,有
个顺序操作⽆法并⾏化,最⼤路径⻓度 也是
。
3、自注意力(self-attention)
在⾃注意⼒中,查询、键和值都是矩阵。考虑缩放的”点-积“注意⼒,其中
矩阵乘 以
矩阵。之后输出的
矩阵乘以
矩阵。因此,⾃注意⼒具有
计算复杂性。正如在图中所讲,每个词元都通过⾃注意⼒直接连接到任何其他词元。因此,有
个顺序操作可以并⾏计算,最⼤路径⻓度也是
。

4、小结
总⽽⾔之,卷积神经⽹络和⾃注意⼒都拥有并⾏计算的优势,⽽且⾃注意⼒的最⼤路径⻓度最短,但是因为其计算复杂度是关于序列⻓度的⼆次⽅(⾃注意⼒具有计算复杂性),所以在很⻓的序列中计算会⾮常慢。







)


)

ojserver)






在EventLoop的任务队列中添加新任务)