目录
引言
波前传感器
编辑
关于相位计算问题补充
关于结构图的修正
光束质量评价指标
Zernike多项式
编辑Zernike多项式法生成相位
光强分布求波前相位-GS
更快的迭代方法SPGD
基于Zernike模式的SPGD
引言
我们还是先从第一篇文献开始理解展开今天分享的一些重要部分。
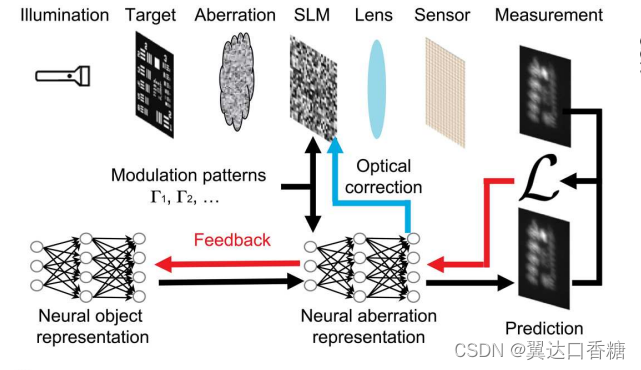
这个部分不详细介绍了,第一次介绍的时候,我感觉这篇文献出现了一些误解。这篇文献提出了这种方法是起源与OA的方法,和第二篇方法其实还不一样。这种方法其实和OA方法是同宗同源的。这次分享还是围绕这次的构架的几个点展开的:
1、波前无传感器自适应调节
2、光束质量评价指标
3、相位问题
4、光强问题
波前传感器
这个调节思路其实和波前整形是不一样的,波前是调节初始光引导光穿过散射介质的研究,而自适应调节更像是波后调节--因为OA的初始用途就是天文学中断流扰动问题。在OA中调节原理还区分有无波前传感器的区别。这种区别更像是反馈调节的信息区别,波前传感器可以探知到波前畸变的信息,而没有波前传感器的话,这是大部分的实验室常见的研究方向。这种方向其实是通过CCD或者其他图像探测设备来优化探测的某一指标。
无波前传感原理图
对探测器采集图像获得的畸变光强分布,利用选取的性能指标,通过波前控制器的控制算法计算得到下一步需要校正的面型,产生控制信号,再由波前控制器驱动校正器(DM)
校正,经过一步步的迭代,使得性能指标朝着极值方向,直至达到我们想要的性能后停止。

有波前传感系统原理图
由波前探测、控制和校正三大部分依次工作,传感器探测波前畸变信息,并传递给控制器使其通过相应的控制算法,产生校正器要施加的控制信号,从而能够实时的校正畸变。相比于前面所讲的无波前探测自适应通过某一性能指标进行迭代,波前校正量与待校正波前畸变之间的相关性不足,导致波前残差收敛慢(校正带宽低),效率低等缺点。而有波前传感器波前校正量是对待校正波前畸变探测后得到的,在理想情况下,两者之间是高度相关的,所以可以通过一次(一个控制周期)校正就能达到较高的精度,实时性高。
因此,这里重点研究指标是无波前传感器叠加图像探测器,所以在正式文案的第一个点就是探讨OA优化指标、波前整形指标、还有最近前沿的优化指标。
关于相位计算问题补充
对于使用CCD设备来说,探测器可以探测强度,其实就根本没办法直接探测到相位的变化的。但是就这个问题而言,其实是在OA领域有解决方案的。这种方案就是利用光强反向算出Zernike多项式,将多种Zernike分量叠加可以生成总的相位。这种方法其实非常有意思,在上面这张结构图的中,是一种神经网络叠加Zernike的相位。
关于结构图的改进
下图是第一次分享的时候制作的SVG图片,当时我第一次认为是同时使用两路神经网络来反向生成图片,这在论文后面附加解释中也是按照这种思路来理解。但是通过阅读OA的理解深入以后,这个相位和光强还可以做一个不一样的处理。首先是我知道了光强可以反推相位,然后是相位可以反推的。那么是不是可以只需要留一个就行了,然后利用这个关系互推就行,这个后面可以再深入再考虑。

光束质量评价指标
最常用的的几种性能指标函数:
1、波前整形性能指标:
2、OA领域五种指标:
1、光强均匀度
光强均匀度定义为平均强度与峰值强度
之比,用于描述激光束近场分布均匀性
2、斯特列尔比(Strehl Ratio)
斯特列尔比(SR)是光束经过有畸变系统后的峰值光强与无畸变系统后
的峰值光强比。即
3、桶中功率比(BQ)
桶中功率比又称环围功率比,定义为相同桶尺寸内理想光斑环围功率与实际
光斑环围功率比的方根值
4、像清晰度函数
像清晰度函数即光斑中的每一点光强平方之和,值越大,表示校正效果越好,
越理想
5、相关系数
相关系数即实际光斑与理想光斑的相似程度,值越大,表示校正效果越好,表达式为
其中为菲涅耳衍射公式计算得到的理想远场光斑分布,
为每次迭代所得的实际光斑分布。相比于其他指标,相关系数指标在收敛效果上差,但其在收敛速度上存在明显的优势。
3、图像引导评价指标
1、熵焓:
2、像素光强:
3、静态指标
4、动态评估
Zernike多项式
Zernike条纹多项式又称为“University of Arizona”多项式,由James C. Wyant教授提出,它属于Zernike标准多项式的另一种表达。 在三维测量中,当真实相位被截断时,真实相位和包裹相位
之间关系如下:
表示真实相位被包裹的过程,可以表示为:
通常,大多数包裹的相位图都是平滑的、连续的,因此真实的相位图可以用一系列正交Zernike多项式进行表示:
式中表示单位圆中定义的第i个Zernike多项式,
表示对应的系数,
(通常设为36)表示多项式的个数。Zernike多项式定义在极坐标下可表示为:
式中代表Zernike多项式径向多项式,
代表距离原点的径向距离,
和
代表角度函数,
代表角度频率,
代表与
轴的夹角。
表示序号,
表示角度频率,
为方位频率
和
是Zernike多项式在极坐标下的一个分量。它与径向多项式
和角度函数的乘积给出了Zernike多项式在极坐标下的值:
Zernike多项式还可以进一步表示为:
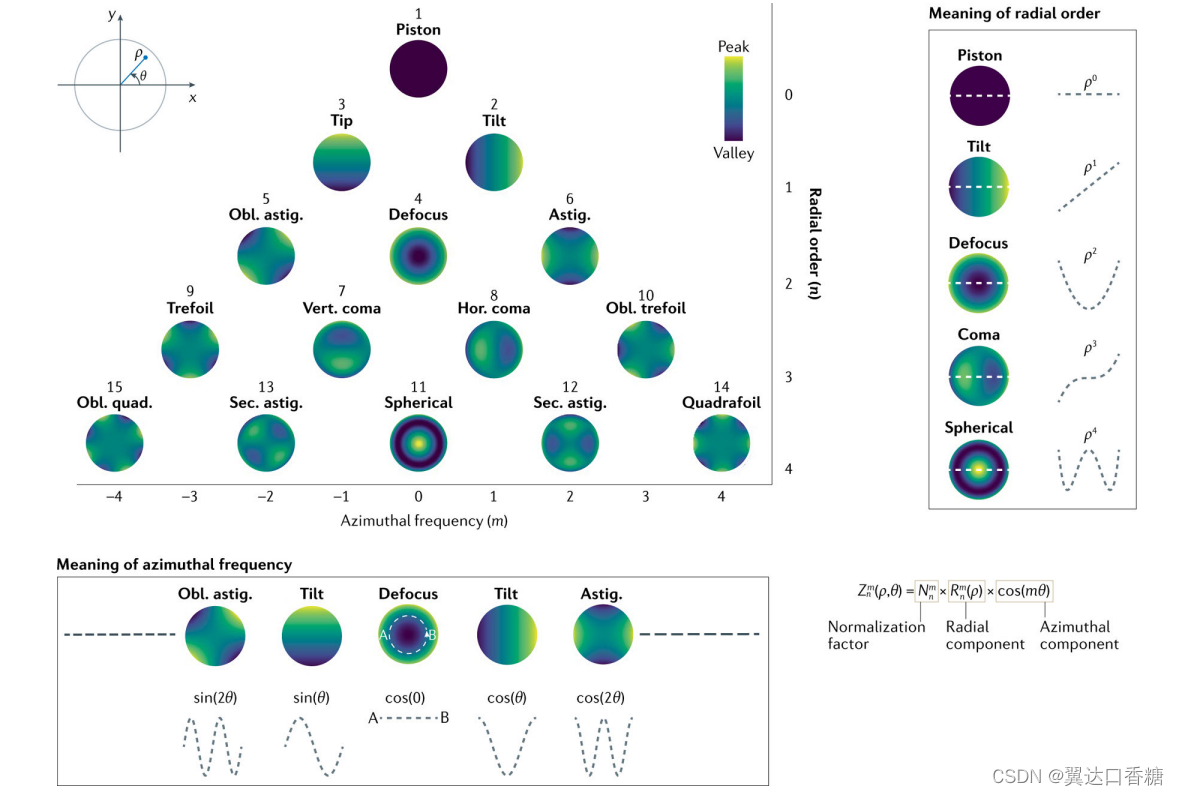
不同阶数的Zernike多项式在极坐标下的表达式,对应于不同的像差。下列是生成的前60阶Zernike像差,可以看出,低阶项较为平滑,细节不足,随着阶数的增加,细节增加。

Zernike像差解析表达式

前60阶Zernike多项式相位分布图
这些多项式根据其径向阶n和方位角频率m进行组织。径向分量描述了多项式如何随半径ρ而变化。例如,径向阶为2的模意味着描述该模的多项式有一个数学项,其中最高幂是2,即它有一个项。正数代表余弦变化,负数代表正弦变化。方位角频率描述了多项式如何随角度
而变化。例如,值为2表示多项式随
而变化。
基于Zernike多项式拟合的相位展开状态空间模型
可以是数学公式公式,也可以是神经网络
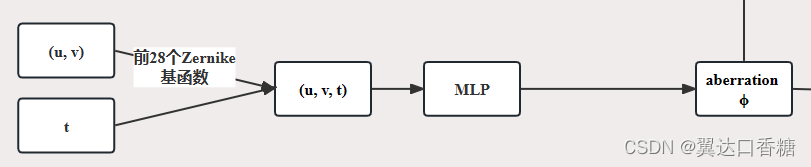
Zernike多项式法生成相位
利用Zernike生成相位屏,不同于傅里叶变换法(功率谱法)生成相位屏,此方法的低频充分,但存在高频不足的问题,需要增加阶数进行补偿。这种方法是从计算各阶系数入手,而非功率谱的相位阵列,要考虑各阶的相关,先通过相位功率谱函数求得协方差
的相位结构函数,当
为奇数数时,协方差为零,为偶数时为
其中为Gamma函数,n、m为第j项Zernike多项式的径向和角向频率数。
可以看出,协方差矩阵不全为零,即Zernike多项式之间并非完全统计独立的,这将为随机数分布的产生带来问题,所以要借助转换,而K-L函数的向量是完全不相关的,作为很好的选择,可以先计算出其独立变量的系数B,再经过转换,得到Zernike系数A
其中是幺正矩阵,且满足
为对角矩阵,
通过奇异值
分解可以求得幺正矩阵X,。
由于Zernike一阶项为活塞像差,不影响相位分布,所以从第二项开始考虑,协方差矩阵
由A和B的关系易的一个新的协方差矩阵
由于S是对角矩阵,所以B是不相关的统计独立的高斯随机变量,均值为零,方差由对角矩S阵给出。
光强分布求波前相位-GS
从如何从测得的光强分布求波前相位的思考,对基于焦平面成像的波前探测技术进行了研究。对近轴传输的波动方程
其中,对光场取共轭后,运算可得
由上式可知,某一平面上的相位分布,可以通过可探测的传输轴上的两个截面的光强分布求得,但解析解难求。1972年,由Gerchberg及Saxton提出了GS算法,算法利用迭代的思想,即由已知的像平面和出瞳上的光强分布作为约束条件,设置循环条件多次迭代得到畸变光束的瞬时相位分布,然后与初始相位做差可得到相位畸变,对相位畸变取共轭后加载至波前校正器可实现畸变校正补偿。
其中为湍流导致的波前畸变,
为计算得到的相位畸变的共轭,
为校正残差。所以校正会有误差存在,可以用校正后的光场分布与理想情况比较,相位畸变误差
其中为校正后光场分布,
为理想光场分布。
已知近场和远场的光强分布,首先给定一个初始相位分布,根据光束而定,一般选为零相位面,与近场振幅分布
构成入射光的复振幅分布
即初始为平面波入射,对其做傅里叶变换,得到焦面复振幅分布
振幅由测得的
替换,再进行傅里叶逆变换得到下一次的迭代的相位,回到公式
,进行新一轮的迭代,直到达到预定的近似程度或迭代次数的条件时,输出此时的相位。
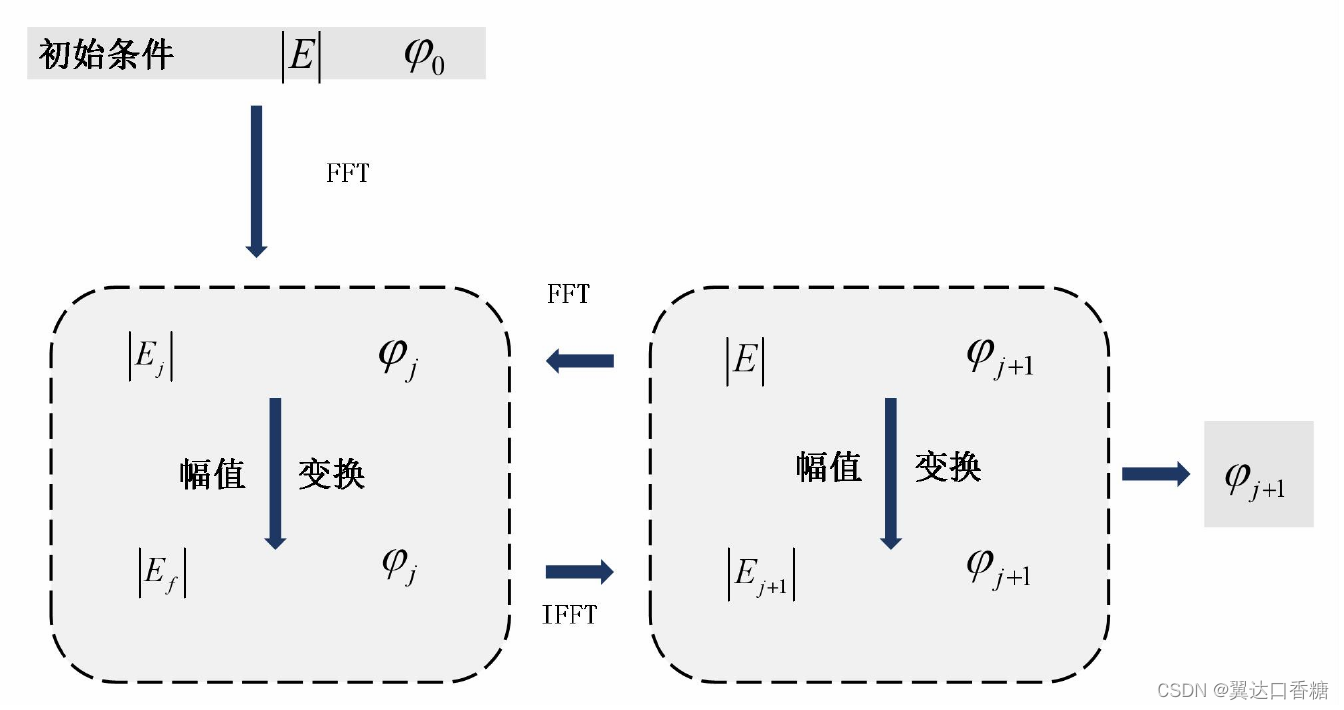
GS算法的具体流程如图所示,下述为传统GS算法的具体实施过程:
两个可测约束条件为:透镜入射前的振幅分布,后焦面的振幅分布
。
(1)对一个振幅为相位随机分布
的光波即物光波进行傅里叶变换,得到像平面的光波。
(2)将得到的像平面的光波的相位保留,振幅由测得的后焦面振幅替换,在进行傅里叶变换。
(3)将得到的近场的相位保留,振幅由测得替换,作为下次迭代初始条件,进行迭代,使得振幅分布不断接近真实值,达到预定的近似程度或迭代次数的条件时,输出此时的相位。
更快的迭代方法SPGD
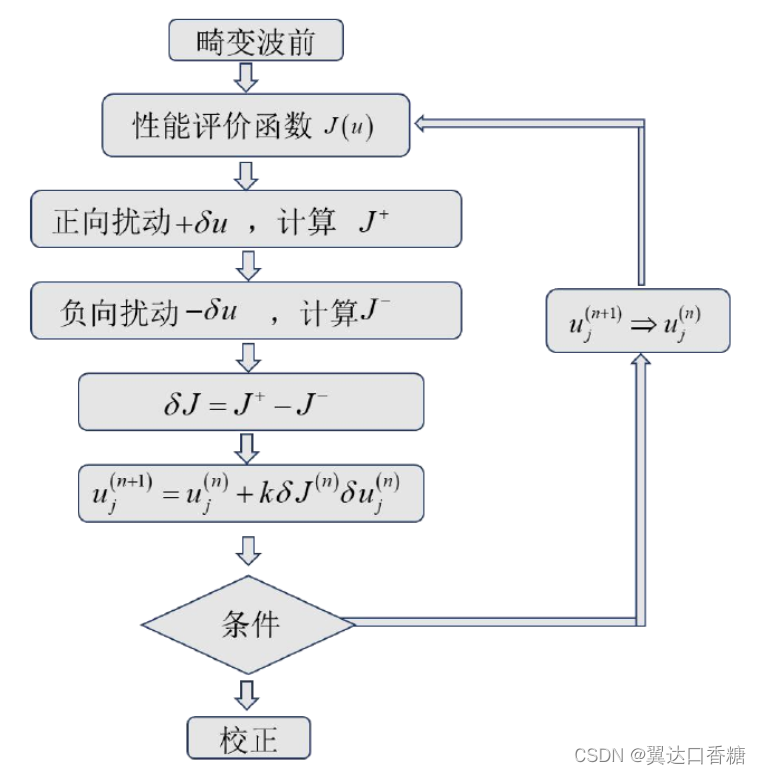
除了上面利用相位信息方法,最常用的就是1997年提出的随机并行扰动梯度下降(SPGD)算法,该算法可调参数少,实现起来较为简单,对动态波前畸变校正效果已经经过多年研究,证实了其效率和优越性。是目前最为常用的无模型控制方法。作为一种盲优化算法,无需知道控制电压与评价函数之间的关系,只需根据性能指标的变化来确定最优的控制电压的搜索方向,每次通过控制电压对变形镜施加随机微小扰动,通用性强,但由于波前校正量与待校正波前畸变之间的相关性不足,需要进行多次迭代计算,因此其收敛速度相对较慢。
对于N个单元的无波前探测的AO系统,将扰动并行施加到N个单元。数学证明,对于相互统计独立且随机的扰动
,在不影响收敛的前提下,可以将各扰动看成伯努利分布,即相同扰动幅值取正负的概率相同
其中为波前校正器的控制信号。系统性能指标
为控制信号
的函数,AO的目标即通过算法迭代获得合适的控制信号,从
得到最优
。性能指标变化
量为
其中k为增益系数,正负由性能指标的决定,性能指标向极大值优化时取正,否则,取负。
基于Zernike模式的SPGD
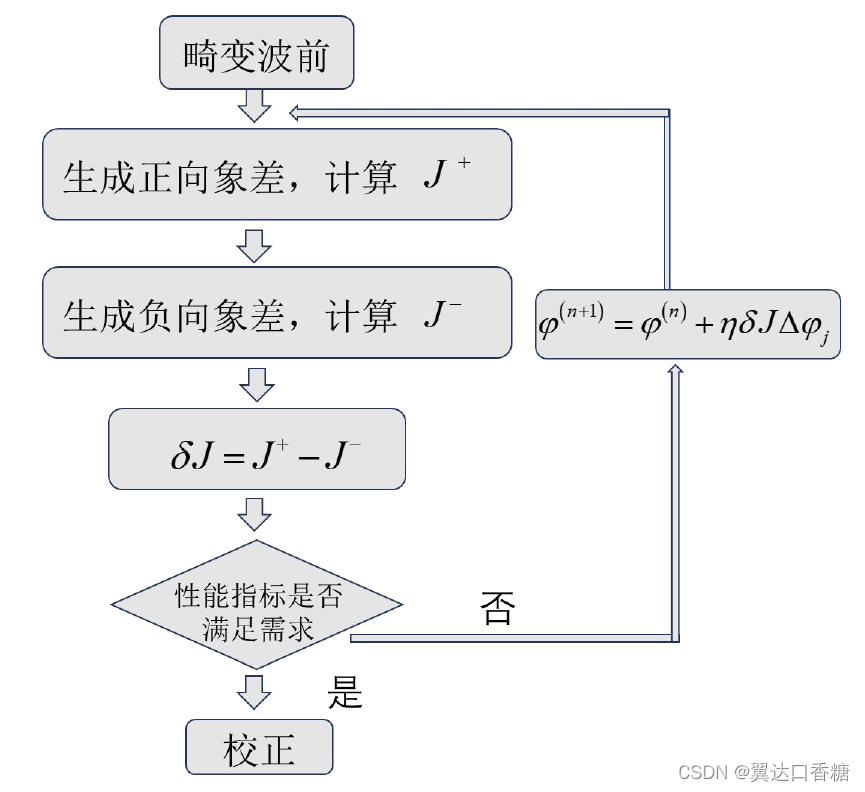
通过Zernike相位屏的生成占比,可以看到,对湍流引起的波前畸变中,低阶像差在湍流中的占比大,权重高,本文基于Zernike多项式的特殊性,提出用Zernike多项式作为扰动项,来优化SPGD算法的迭代次数。对低阶像差进行迭代,速度快、适用范围广、实验工作量小,对第i阶Zernike像差校正,分别生成此阶数的正负单位像差,利用变形镜拟合Zernike像差,根据探测的光斑信息,判断性能指标的变化,生成下一次迭代的面型,原理与传统的相同,只是扰动对象由变形镜拟合的连续的Zernike像差代替由变形镜随机驱动器的电压。

)

)
















