一、7种算法简介
1、红狐优化算法RFO
2、蜣螂优化算法DBO
3、哈里斯鹰优化算法HHO
4、麻雀搜索算法SSA
5、差分进化算法DE
6、灰狼优化算法GWO
7、鱼鹰优化算法OOA
二、CEC2017简介
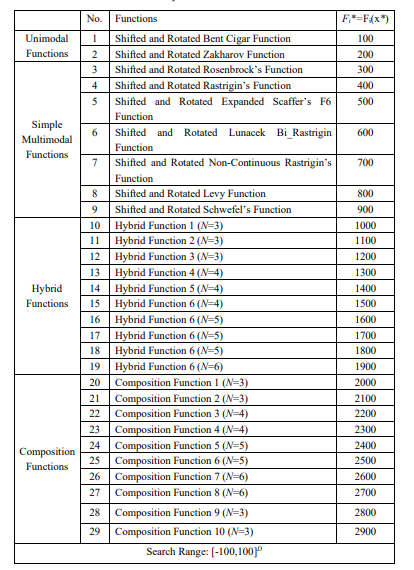
参考文献:
[1]Awad, N. H., Ali, M. Z., Liang, J. J., Qu, B. Y., & Suganthan, P. N. (2016). “Problem definitions and evaluation criteria for the CEC2017 special session and competition on single objective real-parameter numerical optimization,” Technical Report. Nanyang Technological University, Singapore.
三、7种算法求解CEC2017
(1)部分Python代码
import cec2017.functions as functions
import numpy as np
import matplotlib.pyplot as plt
from RFO import RFO
from SSA import SSA
from OOA import OOA
from DBO import DBO
from DE import DE
from GWO import GWO
from HHO import HHO
plt.rcParams['font.sans-serif']=['Microsoft YaHei']
#主程序
function_name =5 #CEC2017 测试函数 1-29
SearchAgents_no = 50#种群大小
Max_iter = 100#最大迭代次数
dim=30;#维度只能是 10/30/50/100
lb = -100*np.ones(dim)#下界
ub = 100*np.ones(dim)#上界
fobj= functions.all_functions[function_name-1]BestX1,BestF1,curve1 = SSA(SearchAgents_no, Max_iter,lb,ub,dim,fobj)#问题求解
BestX2,BestF2,curve2 = OOA(SearchAgents_no, Max_iter,lb,ub,dim,fobj)#问题求解
BestX3,BestF3,curve3 = DBO(SearchAgents_no, Max_iter,lb,ub,dim,fobj)#问题求解
BestX4,BestF4,curve4 = DE(SearchAgents_no, Max_iter,lb,ub,dim,fobj)#问题求解
BestX5,BestF5,curve5 = GWO(SearchAgents_no, Max_iter,lb,ub,dim,fobj)#问题求解
BestX6,BestF6,curve6 = HHO(SearchAgents_no, Max_iter,lb,ub,dim,fobj)#问题求解
BestX7,BestF7,curve7 = RFO(SearchAgents_no, Max_iter,lb,ub,dim,fobj)#问题求解
#画收敛曲线图
Labelstr=['SSA','OOA','DBO','DE','GWO','HHO','RFO']
Colorstr=['r','g','b','k','c','m','y']
if BestF1>0:plt.semilogy(curve1,color=Colorstr[0],linewidth=2,label=Labelstr[0])plt.semilogy(curve2,color=Colorstr[1],linewidth=2,label=Labelstr[1])plt.semilogy(curve3,color=Colorstr[2],linewidth=2,label=Labelstr[2])plt.semilogy(curve4,color=Colorstr[3],linewidth=2,label=Labelstr[3])plt.semilogy(curve5,color=Colorstr[4],linewidth=2,label=Labelstr[4])plt.semilogy(curve6,color=Colorstr[5],linewidth=2,label=Labelstr[5])plt.semilogy(curve7,color=Colorstr[6],linewidth=2,label=Labelstr[6])
else:plt.plot(curve1,color=Colorstr[0],linewidth=2,label=Labelstr[0])plt.plot(curve2,color=Colorstr[1],linewidth=2,label=Labelstr[1])plt.plot(curve3,color=Colorstr[2],linewidth=2,label=Labelstr[2])plt.plot(curve4,color=Colorstr[3],linewidth=2,label=Labelstr[3])plt.plot(curve5,color=Colorstr[4],linewidth=2,label=Labelstr[4])plt.plot(curve6,color=Colorstr[5],linewidth=2,label=Labelstr[5])plt.plot(curve7,color=Colorstr[6],linewidth=2,label=Labelstr[6])plt.xlabel("Iteration")
plt.ylabel("Fitness")
plt.xlim(0,Max_iter)
plt.title("CEC2017-F"+str(function_name))
plt.legend()
plt.savefig(str(function_name)+'.png')
plt.show()
#
(2)部分结果
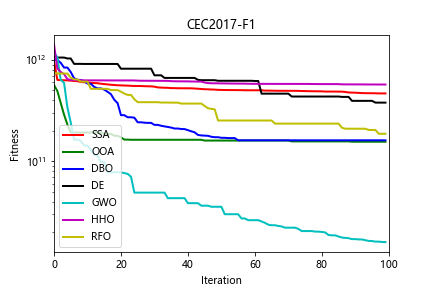


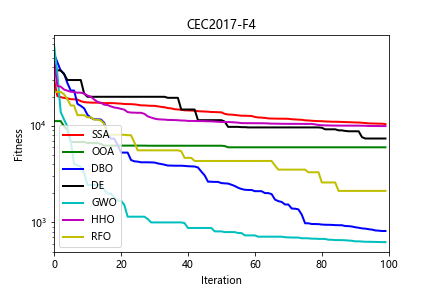
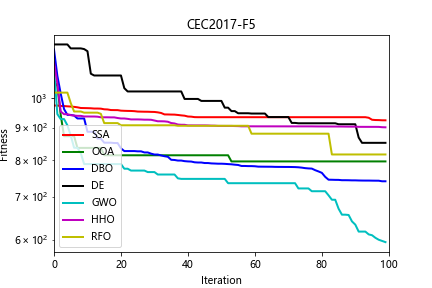
四、完整Python代码








| 在RAG管道中实现上下文压缩和过滤)



—— 代码的使用)





)

