对于环境中的静态障碍物,我们构造几何自由空间来约束自我车辆的完整模型以保证安全。
对于动态障碍物,我们使用凸多边形来覆盖其形状。
然后,我们约束小车与障碍物多边形在每一时刻的符号距离[1]的下界近似,以保证小车的安全。
最小控制努力轨迹类[2]用于参数化轨迹以加快优化过程。
进一步,将原约束规划问题转化为无约束规划问题,并采用拟牛顿方法[3]进行鲁棒求解。
第三节介绍了自动驾驶汽车的时空轨迹规划。
瞬时状态约束和动态避障约束分别在第四节和第五节讨论。
在第六节中,我们重新表述了轨迹优化。
VII给出了基准和真实世界的实验。本文在第八节结束。
讨论了完整的运动规划流水线,并介绍了类车机器人的差分平面模型。然后,我们给出了平面输出空间中考虑人的舒适性、执行时间和可行性约束的轨迹优化问题的表达式。
最后分析了该问题的梯度传播链,为后续的数值优化提供了依据。
时空最优轨迹规划
A.规划管线
整个管道采用分层结构,如图3所示。在实际应用中,建议的规划器与前端规划器合作,前端规划器的主要作用是提供初始猜测。在结构化的道路环境中,我们的规划师被整合到一个多层的规划框架中[19],其中行为策略规划器用于提供前端输出。在没有参考线的非结构化环境中,我们采用轻量级hybridA*算法寻找无碰撞路径,并由所提出的规划器进一步优化。我们定义了一个额外的变量η∈{−1,1}来表征运动方向,η =−1和η = 1分别表示车辆的前后运动。此外,η由前端输出决定,并在后端优化过程之前加上前缀。
B.差分平面车辆模型
本文采用了简化的自行车运动模型
用笛卡尔坐标系来描述四轮车辆。
假设汽车为前轮驱动和转向,具有完美的滚动和无打滑,模型如图4所示。状态向量为
其中为后轮中心位置,v为车身框架的纵向速度,at为经度加速度,an为纬度加速度,φ为前轮转向角度,κ为曲率。
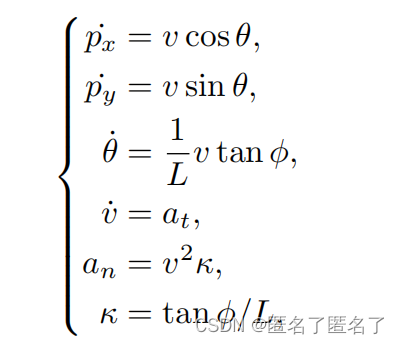
其中L是汽车的轴距长度,CoG是重心的缩写。由于对差分平面汽车模型的深入研究[51],我们选择平面输出为具有物理意义,σ = p是汽车后轮中心的位置。除px、py外,其他变量变换可表示为:
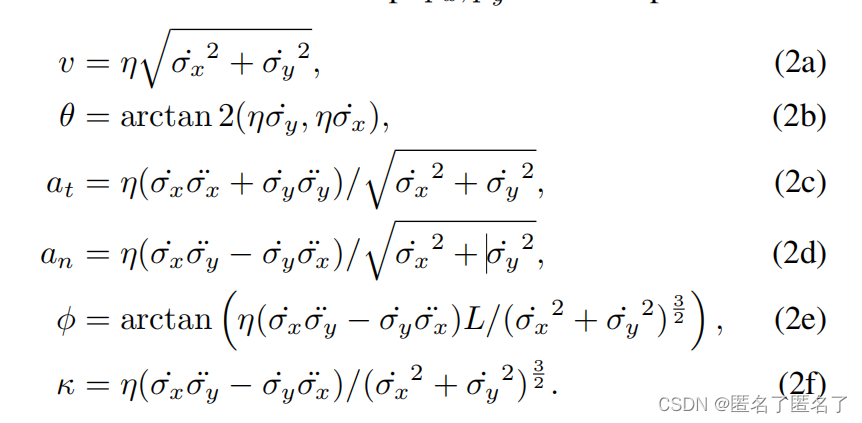
因此,利用自然的微分平坦性,我们可以利用平坦输出及其有限导数来表征车辆的任意状态量,从而简化了轨迹规划,便于优化。
C.整车平坦输出优化方案
其中n为轨迹段的数目,β(t)为自然基。系数矩阵
然后,轨迹第i段的第j段可写为 ,
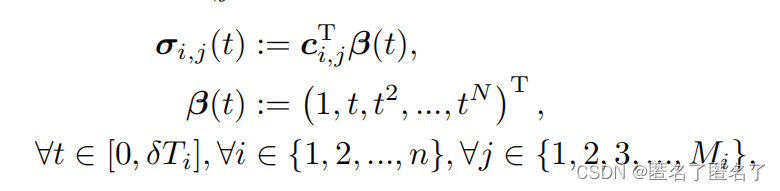
考虑避障约束和动态可行性约束,涉及时间正则化的最小控制努力问题可以表示为非线性约束优化:
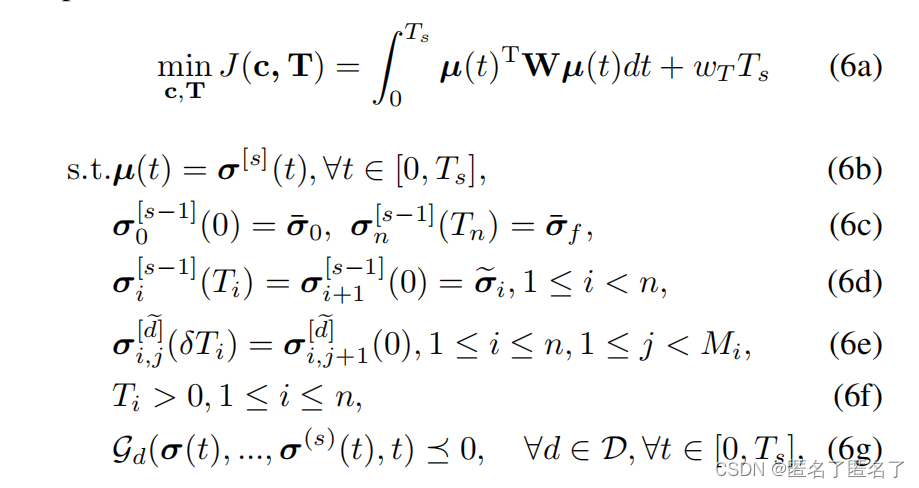
是一个惩罚控制的对角线矩阵。
等式(6c)为边界条件
特定的约束条件等式(6d)
D = {d: d = v,at,an,κ,ζ,Θ}包括动态可行性(v,at,an,κ)、静态和动态避障(ζ,Θ)
可行性约束条件等式(6g)施加在整个轨迹
D.梯度推导
瞬时状态约束
A.动态可行性
经度速度限制:对于自动驾驶,由于交通规则、物理车辆性能和环境不确定性等实际因素,经度速度总是需要限制在一个合理的范围内。然后,将在一个约束点处的经度速度的约束函数定义如下
B. 避免静态障碍
在本小节中,我们分析地提出了基于环境中自由空间的几何表示的有效可计算的静态安全约束。首先对语义环境进行分解,提取安全空间,构造一个由一系列凸多边形组成的驾驶走廊。然后,推导了在行驶走廊中建立全车模型的充分必要条件,并用于构造静态无碰撞约束
在进行特定的推导之前,我们将介绍约束建模的管道。我们首先将前端生成的无碰撞路径离散为与后端优化中约束点数量相同的采样点。然后,结合环境信息,利用[60]方法或根据采样点直接展开生成自由凸多边形。因此,通过将全车辆模型限制在8个约束点,每个约束点限制到相应的凸多边形,保证了整个轨迹是安全的.
还可以与其他常见的地图表示相结合,以保证静态避障,如欧几里得符号距离场(ESDF)。直观地说,我们可以从ESDF地图中获得梯度信息,以推动车辆的整个刚体远离障碍物
动态避障
动态回避约束函数的动态回避约束函数。
A.距离表示
B. 对动态避障的约束






| 在RAG管道中实现上下文压缩和过滤)



—— 代码的使用)





)


