前言

B树和B+树属于树形查找算法中的一种，主要用于数据库系统、文件系统和磁盘存取等方面，都是用于存储和索引大量的数据，以提高检索效率。例如，在磁盘存储中，通过将数据分散到多个磁盘块中，并使用树形结构来组织这些磁盘块，从而提高了查找速度和查找效率。若设B树中所有结点的孩子结点个数的最大值为m，则该B树是一棵m阶B树，另外B+树则是B树的变形。

一、B树

（一）B树的概念

二叉排序树也称为查找树（注意：与二分查找的判定树不同），其中各结点值的大小关系是：左子树<根结点<右子树，且左、右子树也是一棵二叉排序树满足其条件。

前面给过二叉查找树的定义，简单的来说，B树是二叉查找树的推广，即一棵m阶B树可看作一棵m叉查找树，但两者有些方面不同，如下：
1、结点与关键字不同：二叉查找树遵循二叉树的原则，每个结点最多只有两个孩子结点，且每个结点只包含一个关键字；而B树的每个结点最多有m个结点，即最多含有m-1个关键字。
2、平衡性：二叉查找树不一定是一棵平衡二叉树，查找过程中查找效率可能随着查找树的结构变化；而B树是一棵多路平衡查找树，通过限制结点的子树和关键字数量，使B树的高度保持相对稳定，从而提高查找效率。B树也正是在保持平衡的前提下能够更高效地处理大量数据，从而非常适合应用在需要高效存储和访问大量数据的场景中。

（二）B树的性质

B树中与二叉查找树相同的性质，二叉查找树各结点值的大小关系是：左子树<根结点<右子树，而B树中关键字的值的大小关系是：子树1<关键字1<子树2<关键字2<子树3…，一棵m阶B树中，除了根结点外所有结点中关键字个数为：⌈m/2⌉-1 ≤ n ≤ m-1。例如，一棵5阶B树中，除了根结点外所有结点中关键字的个数为2 ≤ n ≤ 4，即关键字个数最少为2，最多为4。

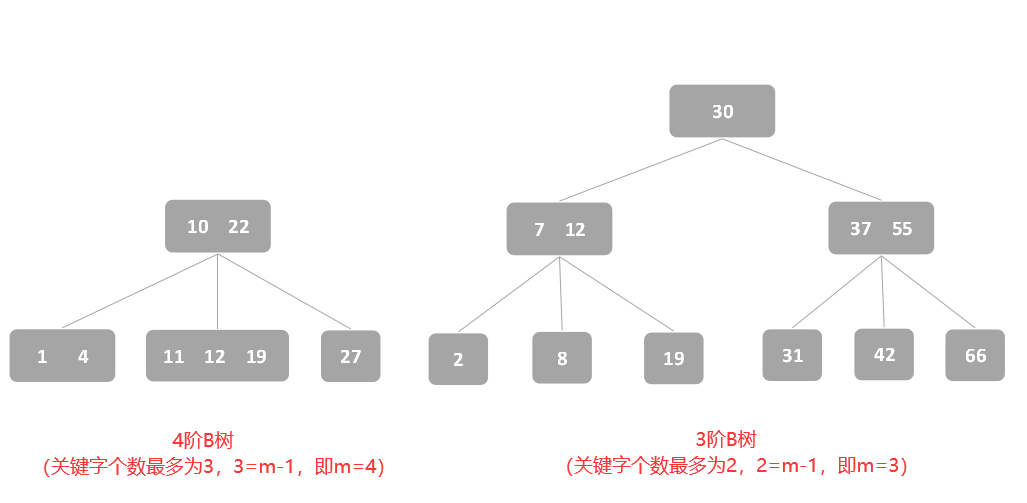
1、m阶B树中，根结点至多有m棵子树，若B树的根结点不是终端结点，则该B树至少有两棵子树。
2、B树中结点内关键字均以升序或降序排列。
3、B树是一棵多路平衡查找树，所有结点的平衡因子均为0。
4、m阶B树中，若根结点没有关键字，则B树无子树，B树为空；若有关键字，由于子树个数等于关键字个数加1，所以子树一定大于或等于两棵。
5、m阶B树中，根结点最少含1个关键字，而除根结点外，每个非叶子结点至少有⌈m/2⌉棵子树，且至少有⌈m/2⌉-1个关键字；由于最少情况下，根结点至少有一个关键字，所以B树中所有结点包括的关键字个数至少为(n-1)(⌈m/2⌉-1)+1个。
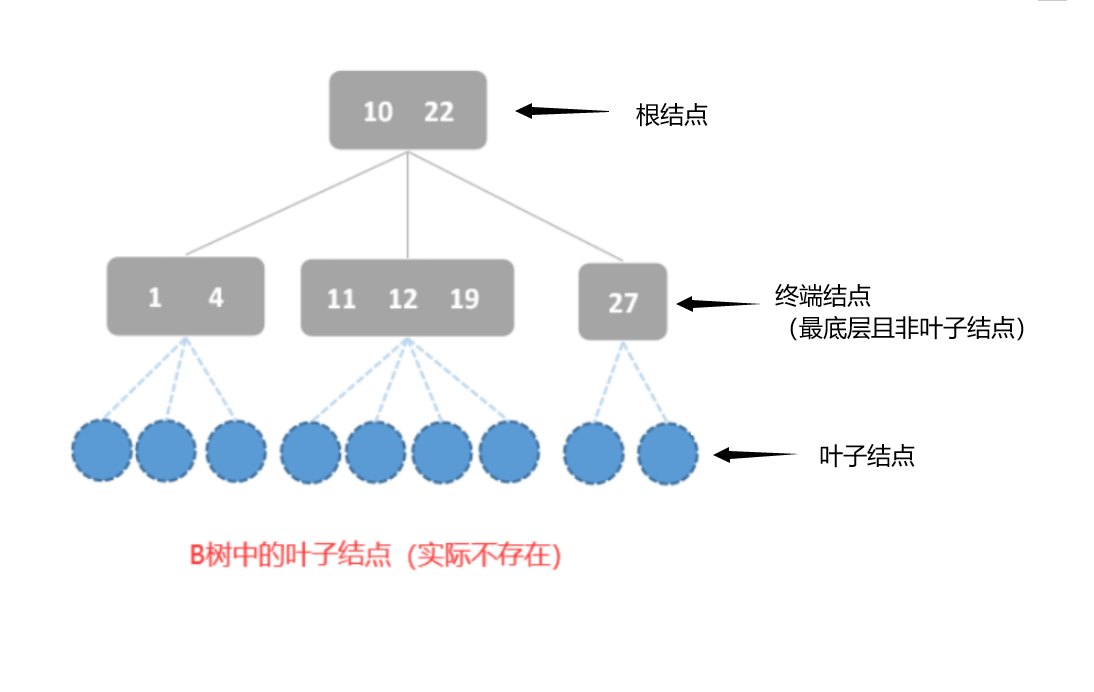
6、结点的孩子结点的个数等于该结点关键字的个数加1，即具有n个关键字的m阶B树，应有n+1个叶结点。另外，B树中所有的叶子结点均在一层上，且不带任何信息，这一点与二分查找判定树中查找失败的结点类似，实际上这些叶子结点不存在，代表查找失败的情况，如下：

（三）B树的高度

在求B树的高度时，不计入叶子结点，若设m阶B树中包括n(n≥1)个关键字，其高度为h，可得到B树的最小高度和最大高度范围区间：log_m(n+1) ≤ h ≤ log_⌈m/2⌉[(n+1)/2]+1。

⌈ ⌉表示向上取整，取比自己大的最小整数，⌊ ⌋表示向下取整，取比自己小的最大整数。

（四）B树的查找

B树的查找类似二叉查找，首先在B树中查找结点，然后在结点所包含的关键字K₁,…,K_n中查找给定的关键字，可通过顺序查找或二分查找进行查找，若找到等于给定值的关键字，则查找成功；否则，继续查找，直至找到或指针为空时，此时查找失败，即查找到B树的叶子结点时失败。

（五）B树的插入

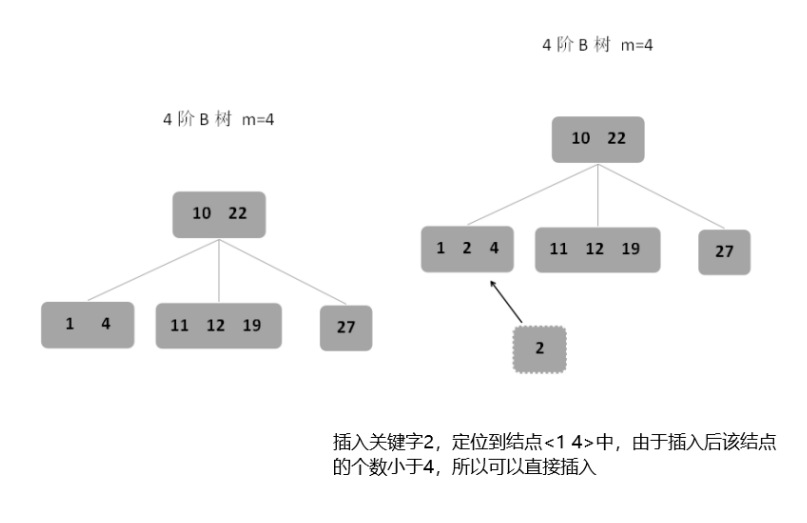
B树的插入操作不仅需要找到要插入的位置（定位），而且需判断插入后是否会导致不满足B树的定义，由于B树中查找成功结点的关键字个数在 ⌈m/2⌉-1 ≤ n ≤ m-1间，如下：
1、第一种情况：若插入后结点的关键字个数小于m，则直接插入。

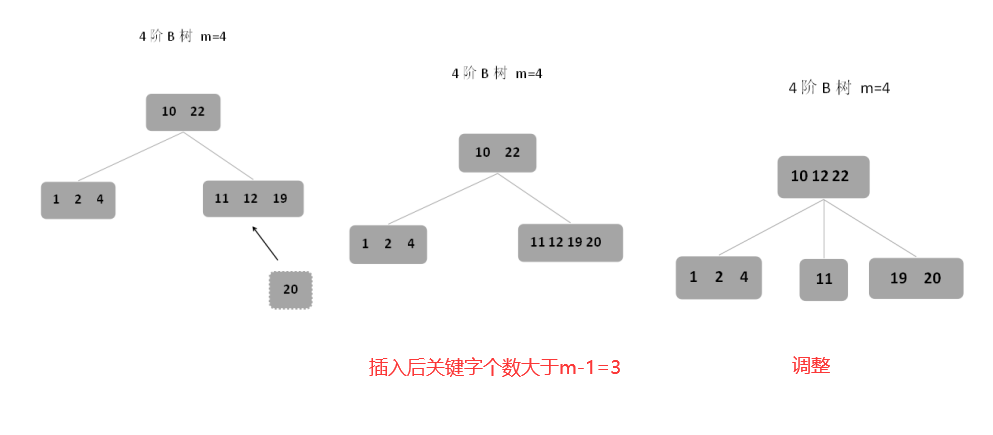
2、第二种情况：若插入后结点的关键字个数大于m-1，则需要进行调整，从关键字中间位置⌈m/2⌉处将关键字分为两部分，左半部分放在原结点中，右半部分放在新的相邻右边结点中，中间关键字元素⌈m/2⌉上移到原结点的父结点中，另外，若父结点的空间也不够，则继续按照以上方式进行调整。

（六）B树的删除

B树的删除分两种情况，如下：
1、第一种情况：
若要删除的关键字在终端结点中时：
（1）若要删除的关键字所在结点的关键字个数大于或等于⌈m/2⌉时，即关键字删除后结点仍满足相应的关键字个数，则可直接删去。
（2）若要删除的关键字当前所在结点的关键字个数等于⌈m/2⌉-1时，且左/右兄弟很充裕时，即其关键字个数大于或等于⌈m/2⌉时，需要进行调整（向兄弟借），用当前结点的前驱/后继、前驱的前驱/后继的后继代替，从而满足B树的定义。

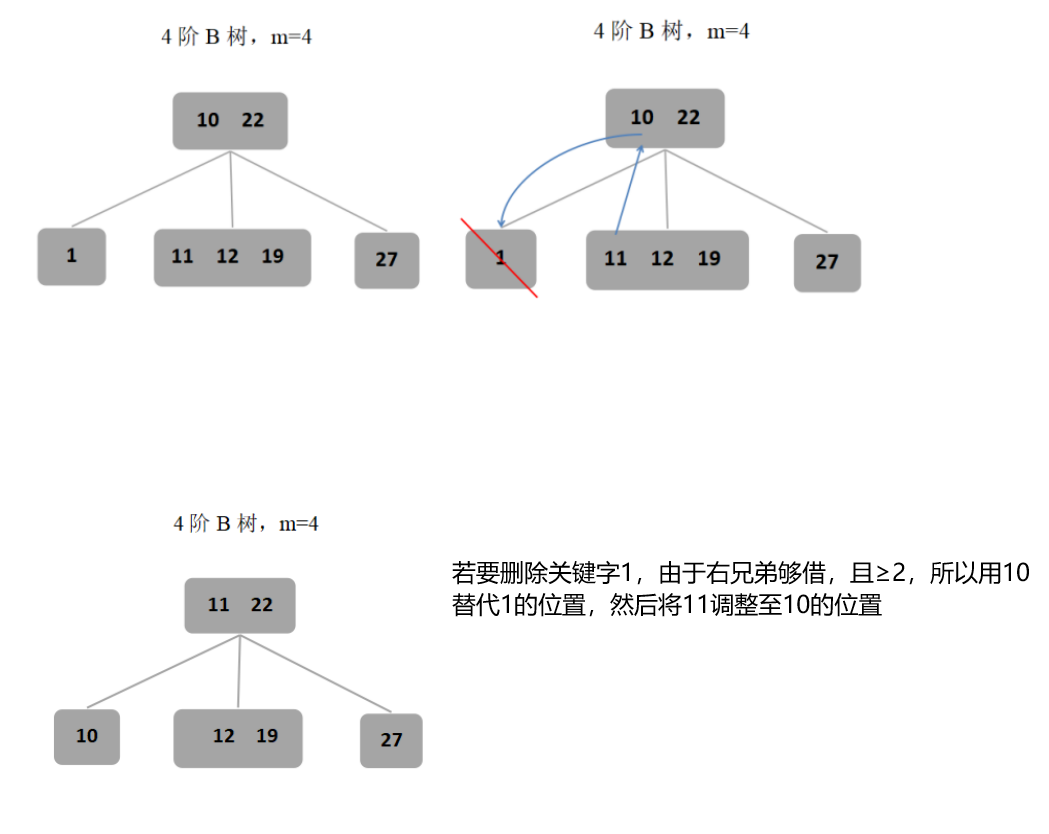
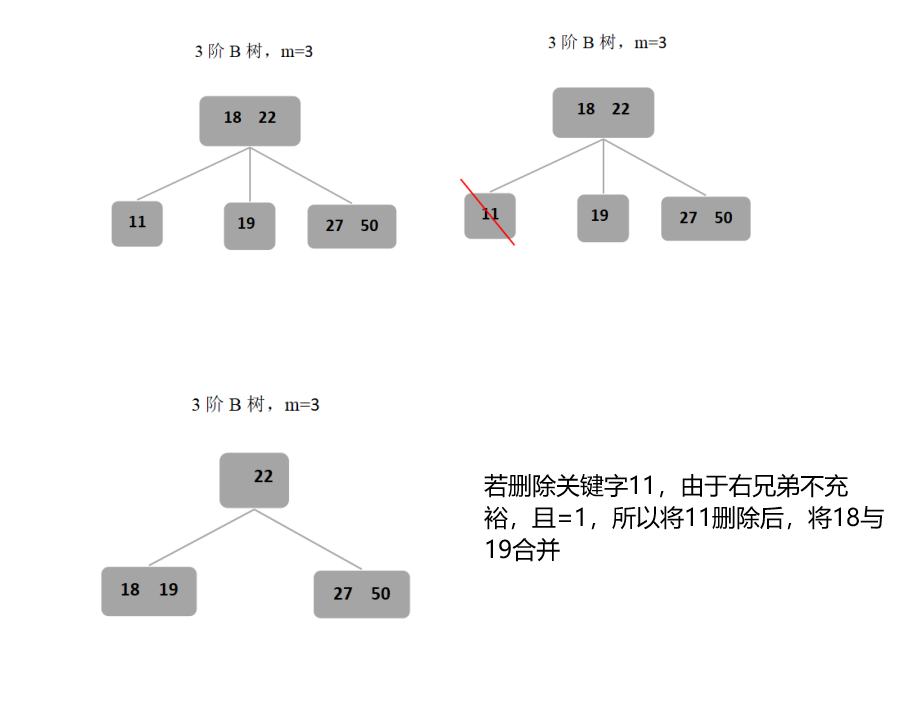
（3）若要删除的关键字当前所在结点的关键字个数等于⌈m/2⌉-1时，且左/右兄弟不是很充裕时，即其关键字个数只等于⌈m/2⌉-1时，则将关键字删除后需要进行合并，即与当前结点的兄弟结点以及双亲结点中的关键字合并。

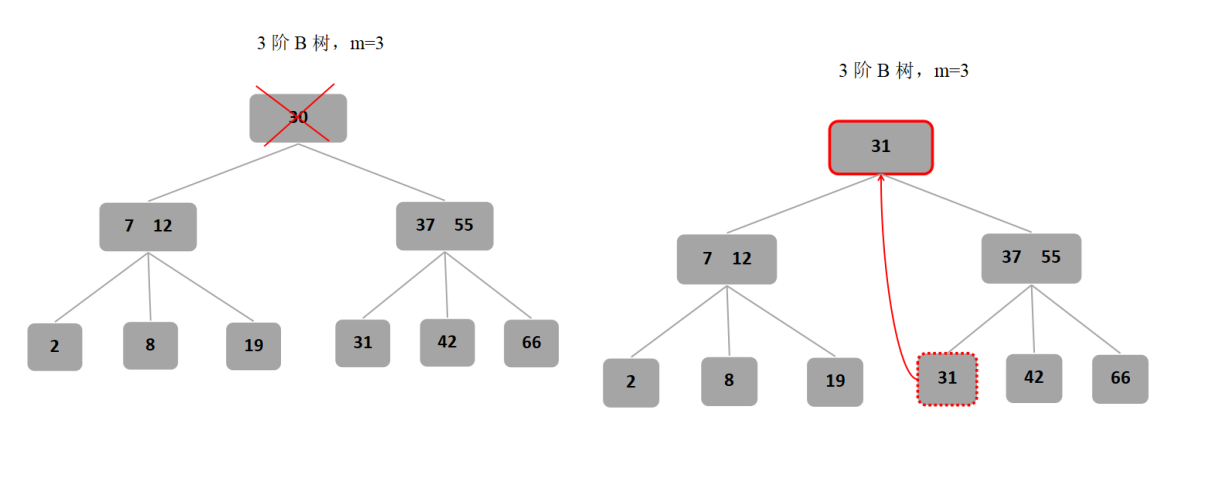
2、第二种情况：
若要删除的关键字不在终端结点中时，用该关键字的直接前驱或直接后继代替，转换成第一种情况，再进行删除。

二、B+树

（一）B+树的概念

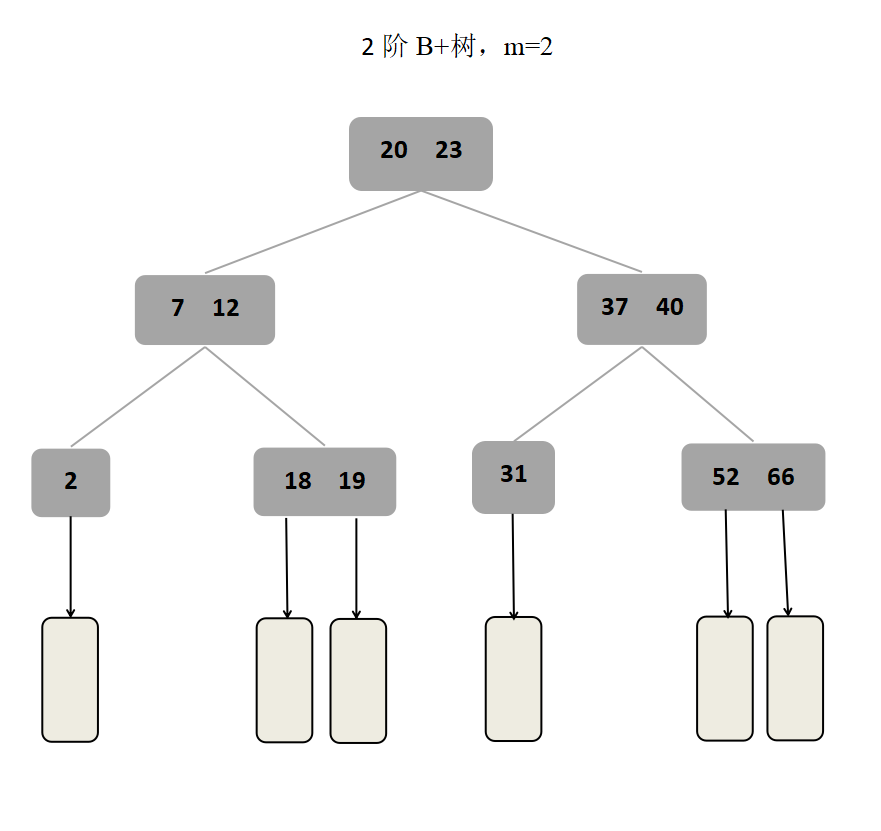
B+树可以由分块查找推广，所以也称为多级分块查找，即m阶B+树，它是B树的变形，与B树相同，B树和B+树都是平衡的多叉树，都用在文件索引结构和数据库索引中，但B+树更加适用。B树的结点包含关键字对应记录的存储地址，且B树中的叶子结点不带信息，而B+树的叶子结点带信息，而其中其他的非叶子结点只是作索引作用。

（二）B+树的性质

B+树中，n个关键字对应n棵子树，即每个关键字对应一棵子树，且子树的个数与结点的关键字个数相等，每个分支结点至少有 ⌈m/2⌉棵子树。

B树与B+树中结点的关键字个数对比如下表：

名称	B树	B+树
根结点关键字个数	1 ≤ n ≤ m-1	2 ≤ n ≤ m
非根结点关键字个数	⌈m/2⌉-1 ≤ n ≤ m-1	⌈m/2⌉ ≤ n ≤ m

（三）B+树的查找

B树支持随机查找，而B+树支持顺序查找和随机查找。

B树不支持顺序查找的原因是查找时可能查找到树中的任何一层，所以其查找速度和稳定性没有B+树高。