
前言
本篇博客讲解数组实现二叉树的顺序结构
文章目录
- 一、二叉树的顺序结构及实现
- 1.1 二叉树的顺序结构
- 1.2 堆的概念
- 1.3 堆的实现
- 1.3.1 初始化堆
- 1.3.2 向堆中插入元素
- 1.3.3 从堆顶删除
- 1.3.4 其他操作
- 1.3.5 完整代码
- Heap.h
- Heap.c
- 1.4 堆的应用
- 1.4.1 堆排序
- 1.4.2 TOP-K问题
一、二叉树的顺序结构及实现
1.1 二叉树的顺序结构
一般来说,顺序结构(数组)通常会用来实现完全二叉树,顺序结构用来实现不完全二叉树不是好的想法,因为会浪费许多空间。

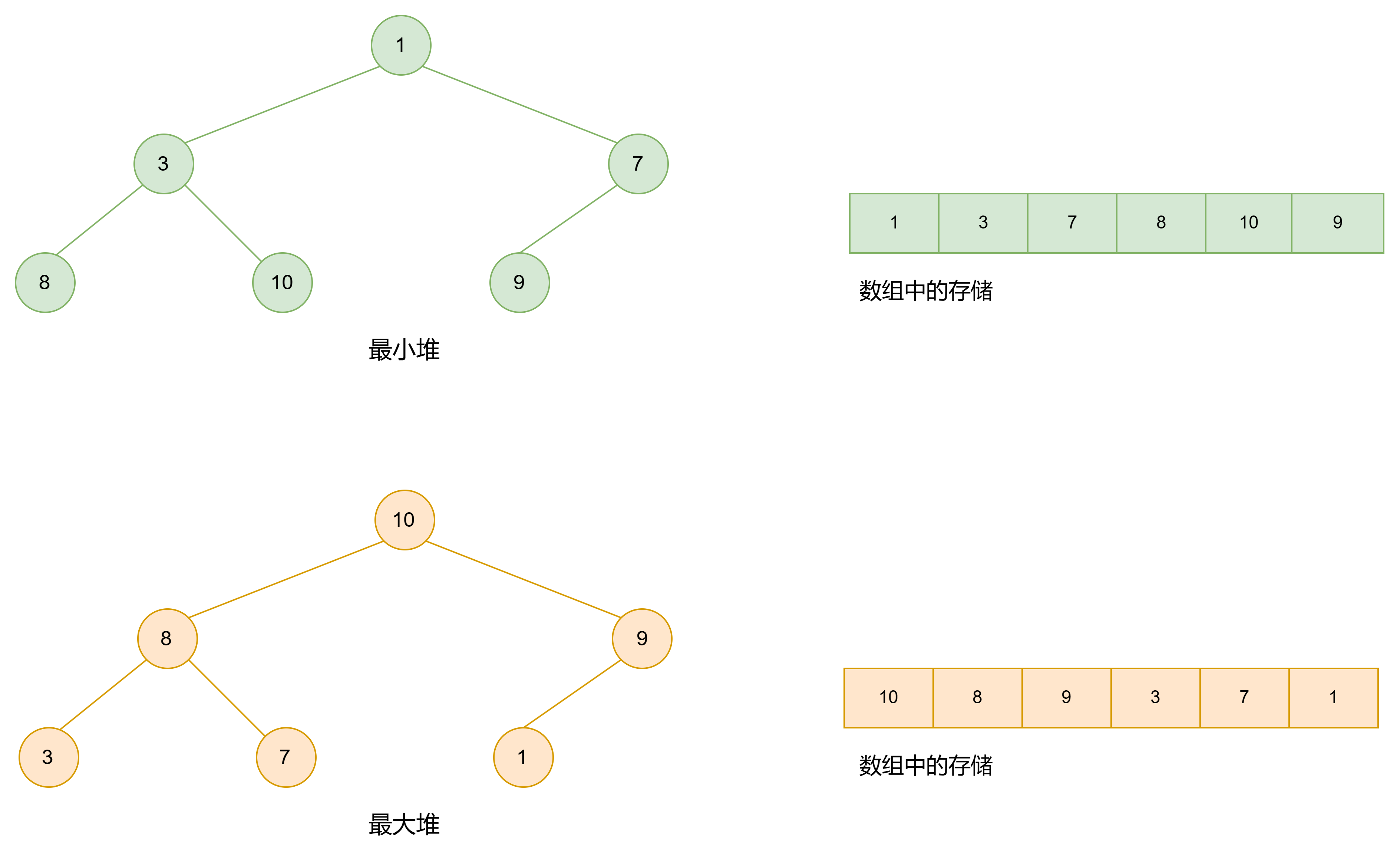
1.2 堆的概念
堆(Heap)是一种特殊的树形数据结构,堆常常被用于优先队列的实现,因为它支持快速查找和删除具有最高或最低优先级的元素。堆分为最大堆和最小堆,这两者都是二叉堆的一种形式。同时堆是完全二叉树。
最大堆和最小堆:
-
最大堆(Max Heap): 在最大堆中,父节点的值大于或等于其每个子节点的值。这意味着树的根节点包含最大的值。
-
最小堆(Min Heap): 在最小堆中,父节点的值小于或等于其每个子节点的值。这样,树的根节点包含最小的值。
堆一般是一个完全二叉树,但并不要求是满二叉树。
1.3 堆的实现
// 堆的数据类型
typedef int HPDataType;// 堆的结构体
typedef struct Heap {HPDataType* a; // 数组,用于存储堆的元素int size; // 当前堆中的元素个数int capacity; // 堆的容量,即数组的大小
} HP;
1.3.1 初始化堆
void HeapInit(HP* php) {assert(php);php->a = NULL;php->size = 0;php->capacity = 0;
}
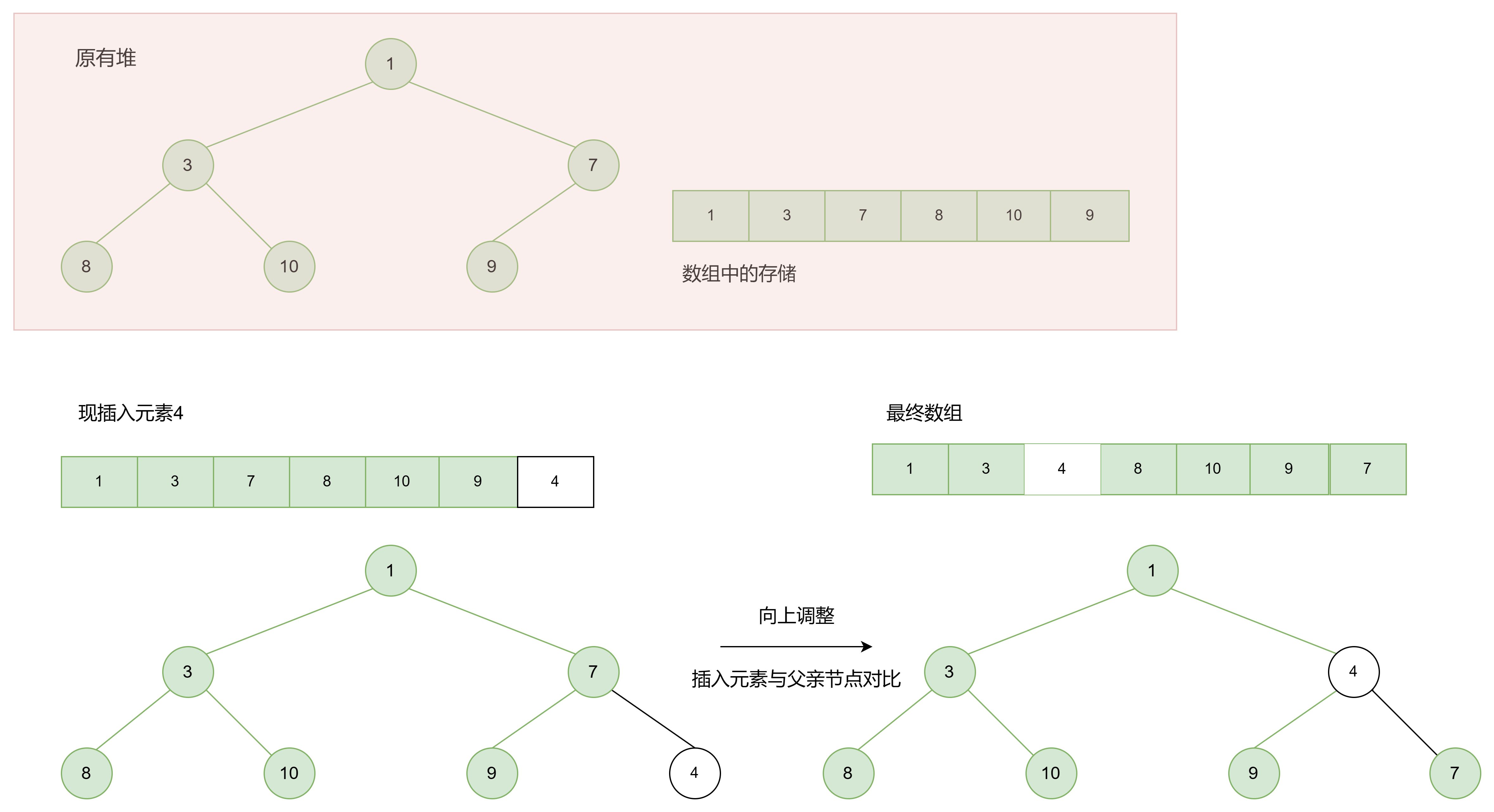
1.3.2 向堆中插入元素
这里以最小堆为例
代码实现:
//元素交换位置
void Swap(HPDataType* p1 , HPDataType* p2) {HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}//向上调整
void AdjustUp(HPDataType* a, int child) {int parent = (child - 1) / 2;//parent为父亲节点while (child > 0) {//a[child] < a[parent]小堆排序;a[child] > a[parent]大堆排序if (a[child] < a[parent]) {Swap(&a[child],&a[parent]);child = parent;parent = (parent - 1) / 2;}else {break;}}
}// 入堆操作
void HeapPush(HP* php, HPDataType x) {assert(php);// 如果堆满了,扩容if (php->size == php->capacity) {int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a , newCapacity * sizeof(HPDataType));if (tmp == NULL) {perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newCapacity;}// 将新元素放入堆尾php->a[php->size] = x;php->size++;// 进行上调操作,保持堆的性质AdjustUp(php->a, php->size - 1);
}
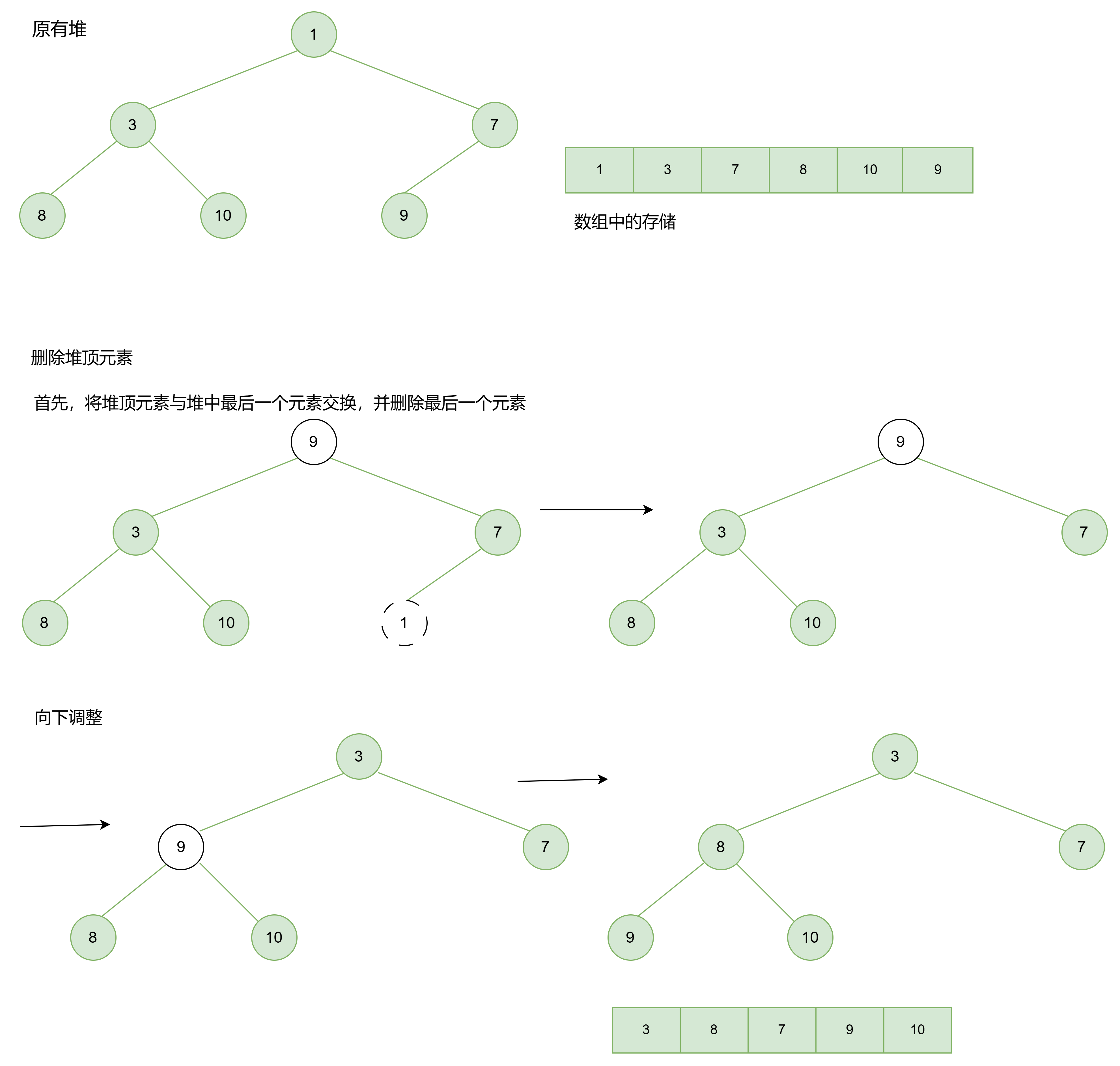
1.3.3 从堆顶删除
删除堆顶元素的思路通常涉及将堆顶元素与堆中最后一个元素交换,然后删除最后一个元素,最后执行一次向下调整(AdjustDown)操作,以维护堆的性质。
代码实现:
//向下调整
void AdjustDown(int* a, int size, int parent) {int child = parent * 2 + 1;while (child < size) {//a[child + 1] < a[parent]小堆排序;a[child + 1] > a[parent]大堆排序if (child + 1 < size && a[child + 1] < a[child]) {++child;}//a[child] < a[parent]小堆排序;a[child] > a[parent]大堆排序if (a[child] < a[parent]) {Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else {break;}}
}//删除堆顶元素
void HeapPop(HP* php) {assert(php);assert(php->size > 0);//堆顶与最后一个元素交换Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}1.3.4 其他操作
//销毁堆
void HeapDestroy(HP* php) {assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}//获取堆顶元素
HPDataType HeapTop(HP* php) {assert(php);assert(php->a);return php->a[0];
}//元素个数
size_t HeapSize(HP* php) {assert(php);return php->size;
}//判断堆是否为空
bool HeapEmpty(HP* php) {assert(php);return php->size == 0;
}1.3.5 完整代码
Heap.h
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>// 堆的数据类型
typedef int HPDataType;// 堆的结构体
typedef struct Heap {HPDataType* a; // 数组,用于存储堆的元素int size; // 当前堆中的元素个数int capacity; // 堆的容量,即数组的大小
} HP;// 初始化堆
void HeapInit(HP* php);// 销毁堆
void HeapDestroy(HP* php);// 向堆中插入元素
void HeapPush(HP* php, HPDataType x);// 从堆中删除元素
void HeapPop(HP* php);// 获取堆顶元素
HPDataType HeapTop(HP* php);// 获取堆的大小
size_t HeapSize(HP* php);// 判断堆是否为空
bool HeapEmpty(HP* php);
Heap.c
#include "Heap.h"void HeapInit(HP* php) {assert(php);php->a = NULL;php->size = 0;php->capacity = 0;
}void HeapDestroy(HP* php) {assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}void Swap(HPDataType* p1 , HPDataType* p2) {HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustUp(HPDataType* a, int child) {int parent = (child - 1) / 2;while (child > 0) {//a[child] < a[parent]小堆排序;a[child] > a[parent]大堆排序if (a[child] < a[parent]) {Swap(&a[child],&a[parent]);child = parent;parent = (parent - 1) / 2;}else {break;}}
}void HeapPush(HP* php, HPDataType x) {assert(php);if (php->size == php->capacity) {int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a , newCapacity * sizeof(HPDataType));if (tmp == NULL) {perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}void AdjustDown(int* a, int size, int parent) {int child = parent * 2 + 1;while (child < size) {//a[child + 1] < a[parent]小堆排序;a[child + 1] > a[parent]大堆排序if (child + 1 < size && a[child + 1] < a[child]) {++child;}//a[child] < a[parent]小堆排序;a[child] > a[parent]大堆排序if (a[child] < a[parent]) {Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else {break;}}
}void HeapPop(HP* php) {assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}HPDataType HeapTop(HP* php) {assert(php);assert(php->a);return php->a[0];
}size_t HeapSize(HP* php) {assert(php);return php->size;
}bool HeapEmpty(HP* php) {assert(php);return php->size == 0;
}1.4 堆的应用
1.4.1 堆排序
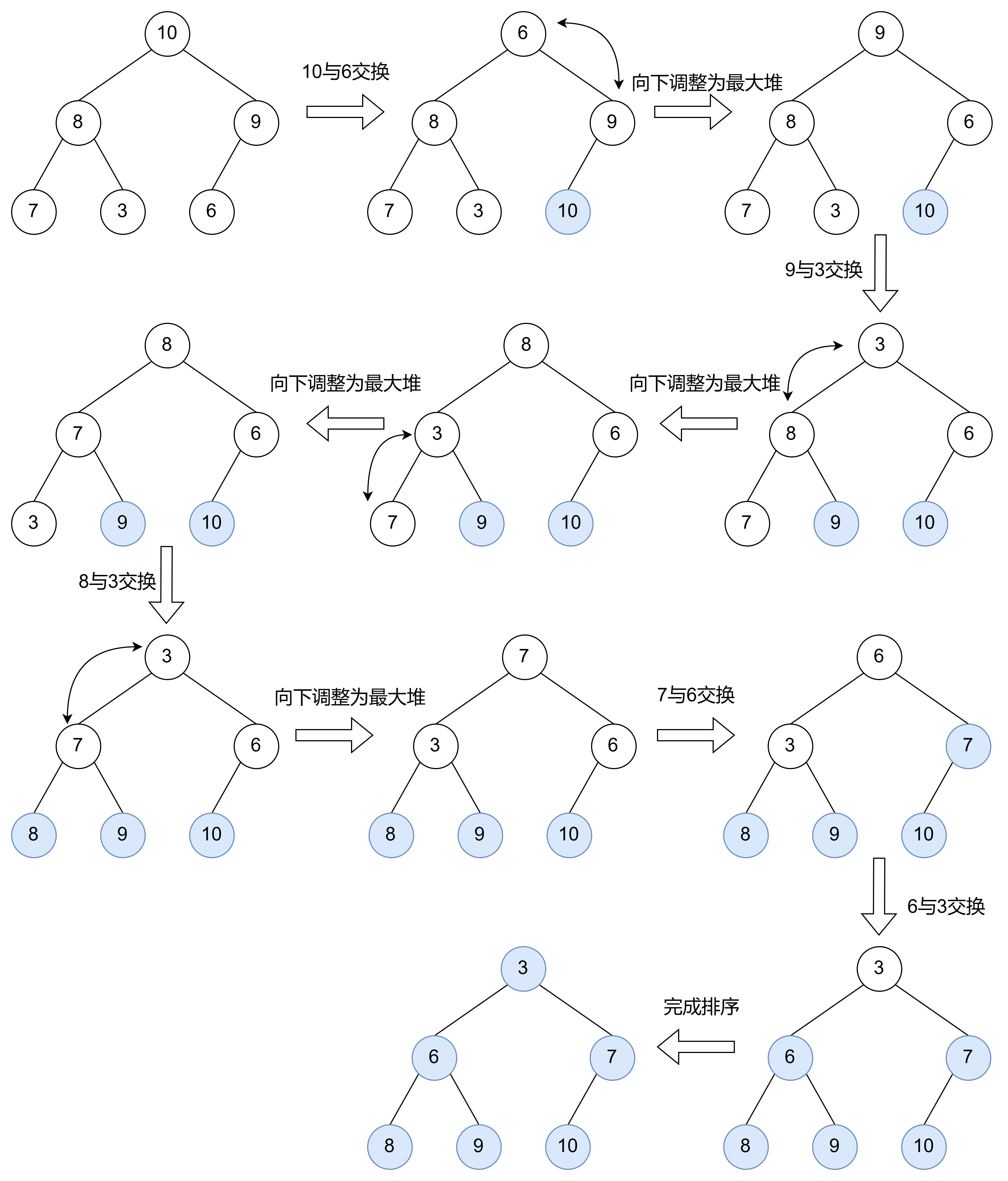
根据堆的特性,可以用堆来进行排序,过程如下:
-
建堆: 将待排序的数组构建成一个最大堆或最小堆。
-
排序: 利用删除堆顶元素的思想,交换堆顶元素(根节点)与数组末尾元素,然后重新调整堆,使其保持最大堆或最小堆的性质。这个步骤只需要执行 n - 1 次,其中 n 是数组的长度。每次执行后,最大(或最小)元素会被移到数组的末尾。重复步骤 2 直到整个数组有序。
代码实现: 基于堆的实现
#include "Heap.h"//降序
void HeapSort(int* a, int n) {//建小堆,向上调整,时间复杂度O(N*logN)for (int i = 1; i < n; i++) {AdjustUp(a, i);}向下调整,时间复杂度O(N)//for (int i = (n - 1 - 1) / 2; i >= 0; --i) {// AdjustDown(a, n, i);//}int end = n - 1;while (end > 0) {Swap(&a[0], &a[end]);//向下调整AdjustDown(a, end, 0);--end;}
}int main() {int a[] = { 1,5,4,3,6,9,10 };int n = sizeof(a)/sizeof(a[0]);HeapSort(a, n);int i = 0;while (i < n) {printf("%d ",a[i]);i++;}return 0;
}
输出结果:

在建立堆时,有向上调整和向下调整两种方式:
//向上调整,时间复杂度O(N*logN)for (int i = 1; i < n; i++) {AdjustUp(a, i);}//向下调整,时间复杂度O(N)for (int i = (n - 1 - 1) / 2; i >= 0; --i) {AdjustDown(a, n, i);}
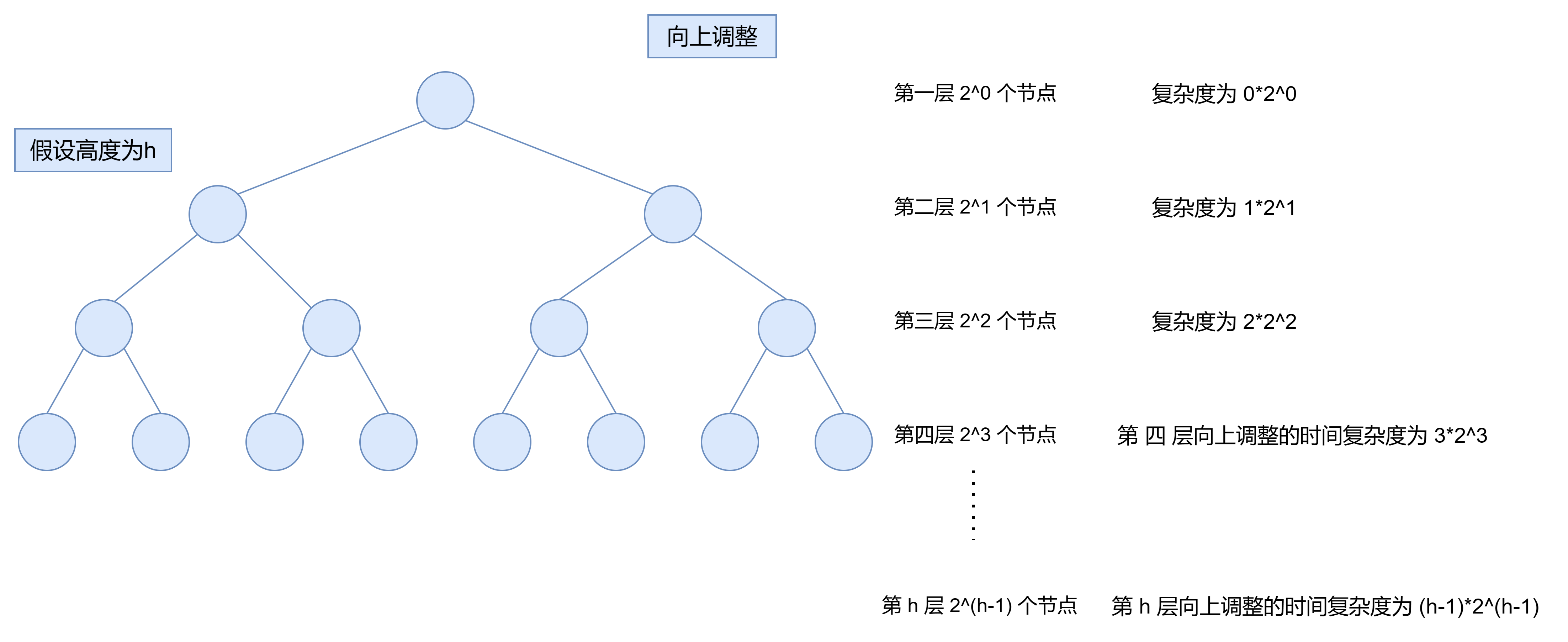
向上调整的时间复杂度为 T ( h ) = 1 × 2 1 + 2 × 2 2 + 3 × 2 3 + . . . . . . + ( h − 1 ) × 2 ( h − 1 ) T(h)=1×2^1+2×2^2+3×2^3+......+(h-1)×2^{(h-1)} T(h)=1×21+2×22+3×23+......+(h−1)×2(h−1),通过错位相减后得到 T ( h ) = − ( 2 h − 1 ) + 2 h ( h − 1 ) + 1 T(h)=-(2^h-1)+2^{h(h-1)}+1 T(h)=−(2h−1)+2h(h−1)+1。
因为树的高度h与节点数N之间的关系是 2 h − 1 = N 2^h-1=N 2h−1=N和
h = l o g 2 ( N + 1 ) h=log_2(N+1) h=log2(N+1)。用N代替h得到,时间复杂度 T ( N ) = − N + ( N + 1 ) ( l o g 2 ( N + 1 ) − 1 ) + 1 , 近似于 O ( N ) = N ∗ l o g 2 N T(N)=-N+(N+1)(log_2(N+1)-1)+1,近似于O(N)=N*log_2N T(N)=−N+(N+1)(log2(N+1)−1)+1,近似于O(N)=N∗log2N

向下调整的时间复杂度为 T ( h ) = ( h − 1 ) × 2 1 + ( h − 2 ) × 2 2 + ( h − 3 ) × 2 3 + . . . . . . + 1 × 2 ( h − 1 ) T(h)=(h-1)×2^1+(h-2)×2^2+(h-3)×2^3+......+1×2^{(h-1)} T(h)=(h−1)×21+(h−2)×22+(h−3)×23+......+1×2(h−1),通过错位相减后得到 T ( h ) = 2 h − 1 − h T(h)=2^h-1-h T(h)=2h−1−h。
同样,用N代替h得到,时间复杂度 T ( N ) = N − l o g 2 ( N + 1 ) , 近似于 O ( N ) = N T(N)=N-log_2(N+1),近似于O(N)=N T(N)=N−log2(N+1),近似于O(N)=N
因此,得出结论,在使用堆进行排序时,利用向下调整法来构建堆更加高效。
1.4.2 TOP-K问题
Top-k 问题是在一组数据中找出前 k 个最大或最小的元素的问题。这个问题在实际应用中经常出现,例如在搜索引擎中找出前 k 个相关度最高的页面,或者在数据分析中找出前 k 个热门商品。
最直观的方法是对整个数据集进行排序,然后取前 k 个或后 k 个元素。这种方法的时间复杂度通常为 O(n log n),其中 n 是数据集的大小。这在 k 远小于 n 的情况下是不划算的。
我们可以通过维护一个大小为 k 的最小堆,可以在 O(n log k) 的时间内找到前 k 个最大元素。
方法如下:
-
创建一个大小为 k 的堆: 初始化一个大小为 k 的堆,如果是求前 k 个最小元素,则使用最大堆(大顶堆),如果是求前 k 个最大元素,则使用最小堆(小顶堆)。
-
将前 k 个元素插入堆中: 遍历数组的前 k 个元素,依次插入堆中。
-
遍历数组的剩余元素: 从第 k+1 个元素开始遍历数组(对于大量数据显然是不合适的,所以可以从文件中挨个读取),对于每个元素,如果它比堆顶元素大(或小,取决于是求最大还是最小元素),则替换堆顶元素,并重新调整堆,以保持堆的性质。
-
输出结果: 遍历堆中的元素,即为前 k 个最大或最小元素。
要在大量数据中找出前k个最大的数字,如果全部放到数组中,所需要的空间很大,因此我们可以生成一个包含大量随机数据的文件。
代码如下:
//头文件中需要包含的头文件
//#include <time.h>// 随机生成大量数据
void CreateDate() {int n = 100000;srand(time(0));const char* file = "date.txt";FILE* fin = fopen(file, "w");if (fin == NULL) {perror("fopen error");return;}for (int i = 0; i < n; i++) {//保证生成的随机数小于100000int x = (rand() + i) % 100000;fprintf(fin, "%d\n", x);}fclose(fin);
}// 从文件中读取数据并输出前k个最大值
void PrintfTopK(const char* file, int k) {FILE* fout = fopen(file, "r");if (fout == NULL) {perror("fopen error");return;}int* heap = (int*)malloc(sizeof(int) * k);if (heap == NULL) {perror("malloc error");return;}// 初始化堆for (int i = 0; i < k; i++) {fscanf(fout, "%d", &heap[i]);AdjustUp(heap, i);}int x = 0;// 逐个读取文件中的数据while (fscanf(fout, "%d", &x) != EOF) {// 如果读取的数比堆顶元素大,则更新堆if (x > heap[0]) {heap[0] = x;AdjustDown(heap, k, 0);}}// 输出前k个最大值for (int i = 0; i < k; i++) {printf("%d ", heap[i]);}free(heap);fclose(fout);
}// 主函数
int main() {// 生成随机数据文件CreateDate();// 输出文件中的前5个最大值PrintfTopK("date.txt", 5);return 0;
}
我们要查看所有的数据,依此判断是否成功找出前k个最大数是不容易的,所以我们在生成的文件中,将5个随机生成的数改成比100000大的数,当我们输出时,只需要检查最大的5个数是不是这几个,即可知道排序是否正确。
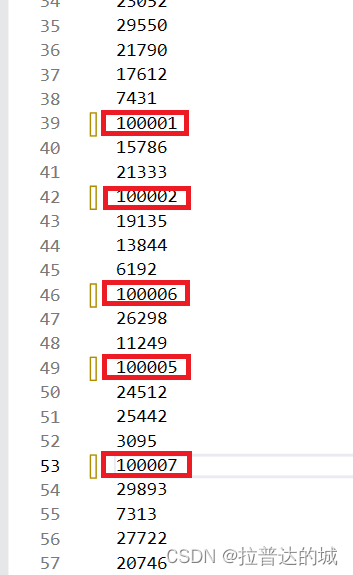
输出结果:


如果你喜欢这篇文章,点赞👍+评论+关注⭐️哦!
欢迎大家提出疑问,以及不同的见解。






常用方法和使用例子)








)

)
)
