CGAL的无限制的Delaunay图

本章描述了构建L∞距离下线段Delaunay图的算法和几何特征。这些特征还包括绘制L∞距离下线段Delaunay图对偶（即L∞距离下线段Voronoi图）边缘的方法。L∞算法和特征依赖于欧几里得（或L2）距离下的线段Delaunay图算法和特征。L∞度量中的分段Voronoi图在VLSI设计中具有应用。

在定义部分，我们给出了一些定义。在软件设计部分，我们解释了算法和特征的设计。

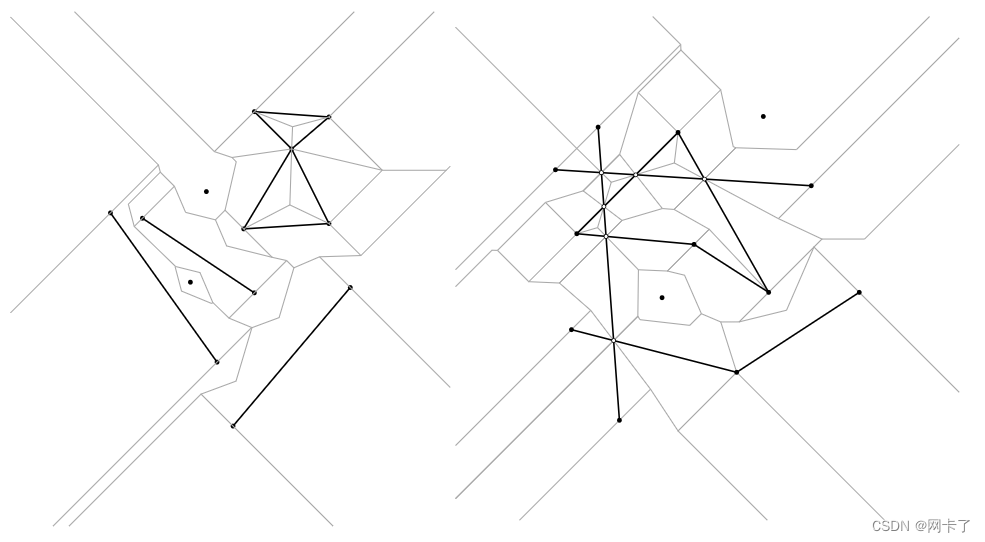
一组弱（左）和强（右）相交点的L∞分段Voronoi图。

1、定义

如果一对分段站点有一个公共点，并且这个公共点不在两个站点的任何内部，则称它们为弱相交。如果一对分段站点相交，并且它们有一个以上的公共点，或者它们的公共点位于两个站点中的至少一个内部，则称它们为强相交。如果一组分段站点中的所有对都是弱相交（强相交）或不相交，则称其为弱相交（强相交）。见图。

给定平面上的两点p=(px,py)，q=(qx,qy)，它们的L∞距离为

d∞（p，q）=max（|px-qx|，|py-qy|）。

不难看出，与定点c相距相等固定L∞距离r的点的几何轨迹是中心为c、边长为2r的轴平行正方形（L2中的类似物是中心为c、直径为2r的圆）。

如果我们假设站点的一般位置，那么两点之间或一点与一段之间的 L∞ 等分线是多边形链；示例见图。这与 L2 沃罗诺伊图形成鲜明对比，其中一点与一段之间的等分线是抛物线弧。在 L∞ 沃罗诺伊图中，如果输入站点的坐标是有理数，则图中的顶点坐标也是有理数，而 L2 图则不是这样。有关 L∞ 等分线和图的更多详细信息，请参见。

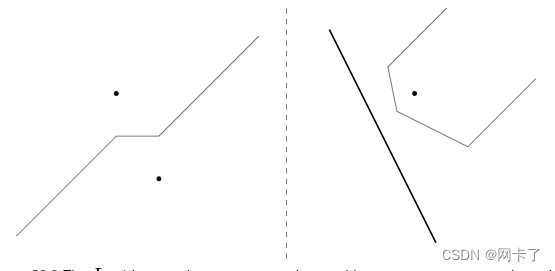
L∞平分两点之间以及线段和点之间的距离。

与L2设置相比，L∞设置中的一个非常重要的区别是，在一些特殊的非一般位置情况下，两个站点之间的L∞平分线可以是二维的。由于这在绘制图表时会产生问题，我们通过将平分线二维区域的一部分分配给平分线的两个站点，对这些平分线进行一维化。此外，在采用L∞图表的VLSI应用中，这种图表的简化是可以接受的。

如果两个不同的点p，q共享一个坐标，则它们的L∞平分线是二维的，如图52.3所示。在这种特殊情况下，我们通过取这两个点的欧几里得平分线来一维化平分线。

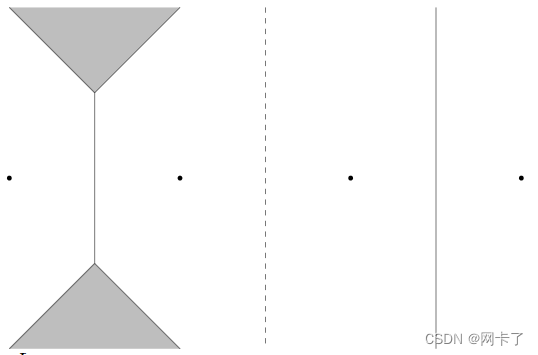
具有相同y坐标的两点之间的L∞平分线及其一维化。

同样地，如图所示，轴平行线段内部与其端点之一之间的平分线也是二维的。我们通过取穿过端点并与线段垂直的线来一维化该平分线。

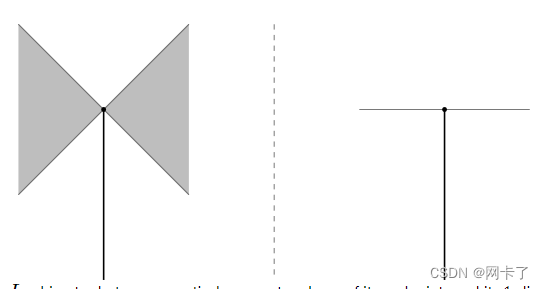
垂直线段与其一个端点之间的L∞平分线及其一维化。

2、软件设计

一般来说，L∞分段Delaunay图的算法和特征的软件设计依赖于L2分段Delaunay图的相应算法和特征。我们将L∞类实现为2D分段Delaunay图包中相应L2类的子类。与相应的L2类相比，L∞类的名称在图后包含额外的_Linf。

L∞图构造的复杂度顺序与L2图相同，因此我们建议最终用户参考[2]进行复杂度分析。

2.1、线段Delaunay图

Voronoi图适配器包中的Voronoi_diagram_2类可用于从L∞段Delaunay图（或层次结构）中获取L∞段Voronoi图。

2.2、线段Delaunay图特征

与L2的情况一样，几何谓词非常复杂，我们不会为最终用户提供细节。我们的实现尽可能重复使用L2特性，但存在很大差异。我们支持几何和算术过滤，就像L2谓词一样。

与L2设置类似，SegmentDelaunayGraphLinfTraits_2概念有四个模型，其中两个支持强相交位点（Segment_Dlaunay_graph_Linf_traits_2、Segment_DLaunay_graph_Linf_filtered_traits_2），并且其中两个不支持交叉位点（Sement_DlaunaY_graph_Linf_traits_without_interctions_2、Segment-Dlaunay_Grah_Linf_ffiltered_trats_without _interctionS_2）。请参阅Delaunay图形包手册的优化内存分配小节，该小节解释了何时使用这些特性中的每一个。