1. 前言

汉诺塔问题是一个经典的递归问题，源于印度的一个古老传说。这个问题的特点是其独特的解决方式，需要将一堆盘子从一个柱子移动到另一个柱子，每次只能移动一个盘子，并且不能将一个较大的盘子放在较小的盘子上面。这个问题的解决方案不仅展示了数学的逻辑美，也为我们提供了一个理解递归和栈结构的好机会。

2. 导入汉诺塔问题

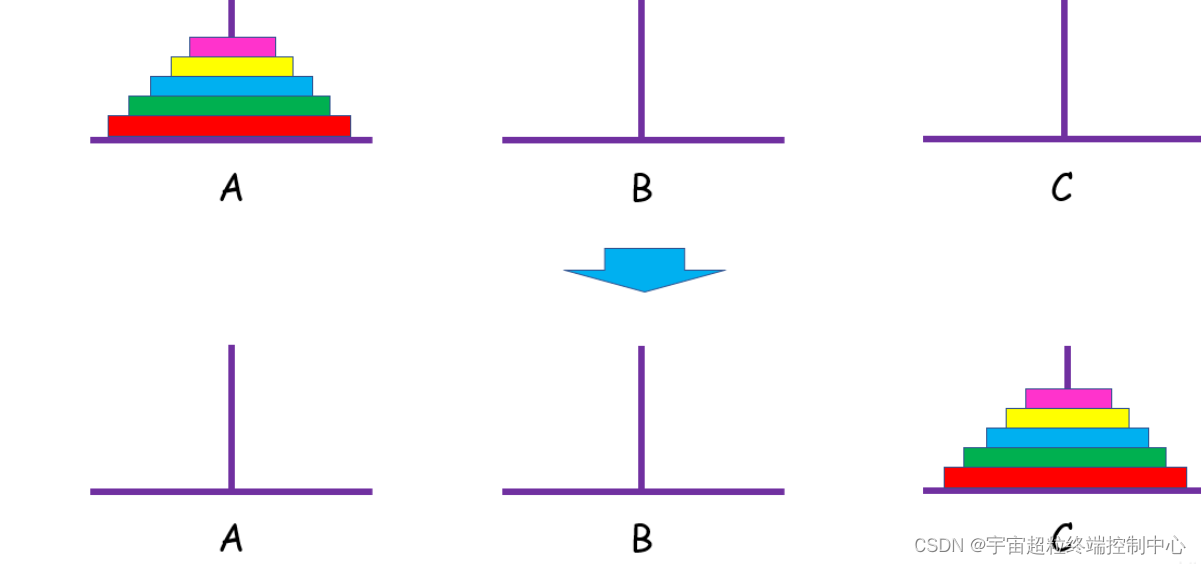
汉诺塔问题的描述如下：有三根柱子，A、B、C。A柱子上从下往上按大小顺序叠放着n个圆盘，目标是将这n个圆盘移动到C柱子上。移动过程中必须遵守以下规则：

1. 一次只能移动一个圆盘。
2. 大圆盘不能叠放在小圆盘上。
3. 可以利用B柱子作为辅助柱子。

对于任何一个具体的步骤，实际上都需要进行3次移动：

• 将上面的 n-1 个盘子从起始柱子（如 A）移到另一个柱子（如 B）；
• 将最大的盘子从起始柱子移到目标柱子（如 C）；
• 最后，将 n-1 个盘子从临时柱子（如 B）移到目标柱子（如 C）。

这种分步骤、分阶段的解决方式正是递归的精髓。在C语言中，我们可以通过定义递归函数来实现这一过程。

3.预备知识

在开始解决汉诺塔问题之前，我们需要了解一些关键概念和基础知识。这些概念将帮助我们更好地理解问题，并为其解决方案打下基础。

递归

递归是函数直接或间接调用自身的一种编程技术。它允许我们将一个复杂问题分解为更小的子问题，并从解决这些子问题开始解决原始问题。在汉诺塔问题中，递归将帮助我们将问题分解为移动一个或没有盘子的小步骤。

栈

栈是一种后进先出（LIFO）的数据结构，用于存储临时数据。它的工作原理类似于一堆盘子，只能从顶部添加或移除元素。在汉诺塔问题中，栈将用于存储需要移动的盘子的柱子编号，以支持递归操作。

通过理解递归和栈的概念，我们可以更好地理解和解决汉诺塔问题。这些概念不仅在解决汉诺塔问题时有用，而且在许多其他算法和数据结构问题中也非常重要。

4.分析讲解

将 A 座上 2 个盘子移到 B 座上（借助 C）
将 A 座上 1 个盘子移到 C 座上
将 B 座上 2 个盘子移到 C 座上（借助 A）

其中第 2 步可以直接实现。第 1 步又可用递归方法分解为：

将 A 上 1 个盘子从 A 移到 C
将 A 上 1 个盘子从 A 移到 B
 将 C 上 1 个盘子从 C 移到 B

第 3 步可以分解为：

 将 B 上 1 个盘子从 B 移到 A
 将 B 上 1 个盘子从 B 移到 C
 将 A 上 1 个盘子从 A 移到 C

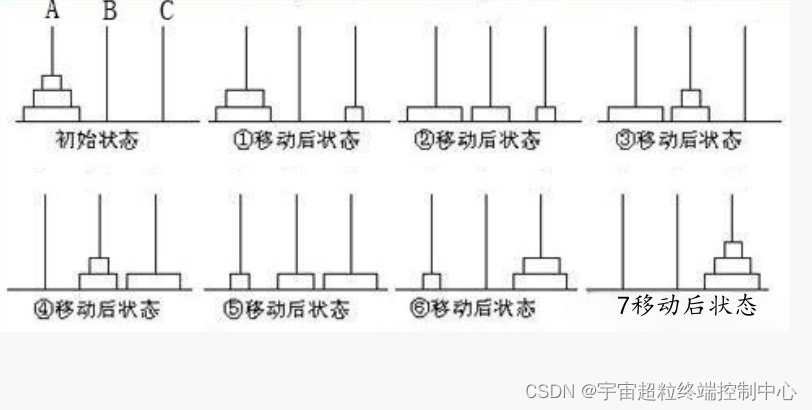
将以上综合起来，可以得到移动 3 个盘子的步骤：

A ->C
A->B
C->B
A->C
B->A
B->C
A->C

共经历了 7 步。
由此可以推出：移动 n 个盘子要经历 2^n-1 步。如移动 4 个盘子需要经历 15 步，移动 5 个盘子需要经历 31 步，移动 80 个盘子需要经历 2^80-1 步。

我们已经知道 3 个盘子如何移动，n 个盘子的移动方法和上面 3 个盘子的移动方法相比，道理是一样的。采用递归的方法解决n 个盘子的移动问题。将 n 个盘子从 A 座移到 C 座可以分解为以下 3 个步骤：

将 A 座上 n-1 个盘子移到 B 座上（借助 C）
将 A 座上剩下的 1 个盘子移到 C 座上
将 B 座上 n-1 个盘子移到 C 座上（借助 A）

上面第 1 步和第 3 步，都是把 n-1 个盘从一个座移到另一个座上，采取的办法是一样的，只是座的名字不同而已。为使之一般化，可以将第 1 步和第 3 步表示为：
将“one”座上 n-1 个盘移到“two”座（借助“three”座）。

5.算法代码

#include <stdio.h>//定义move函数，将一个盘子从x座移到y座上 
void move(char x, char y)
{printf("%c-->%c\n",x,y);   //输出移盘方案。x,y代表A，B，C座之一，根据每次的不同情况分别取A，B，C代入 
}void hanoi(int n, char one, char two, char three) //将n个盘从one座借助two座，移到three座 
{if(n==1)move(one, three);else{hanoi(n-1, one, three, two); //将 A 座上 n-1 个盘子移到 B 座上（借助 C）move(one, three);//将 A 座上剩下的 1 个盘子移到 C 座上hanoi(n-1, two, one, three);//将 B 座上 n-1 个盘子移到 C 座上（借助 A）} } main()
{int m;printf("input the number of disks:");scanf("%d",&m);   //盘子的数量 printf("The step to moving %d disks:\n",m);hanoi(m,'A','B','C');}

运行示例结果：

input the number of disks:3
The step to moving 3 disks:
A-->C
A-->B
C-->B
A-->C
B-->A
B-->C
A-->C