目录
1.课题概述
2.系统仿真结果
3.核心程序与模型
4.系统原理简介
4.1 双闭环PI控制器设计
4.2 SVPWM技术
4.3 控制系统实现
5.完整工程文件
1.课题概述
基于双闭环PI和SVPWM的PMSM控制器simulink建模与仿真。系统包括逆变桥、PMSM、park变换、clark变换、SVPWM、PI控制器、信号测量等单元模块的Simulink模型。在这个模型中,我们将实现双闭环控制——转速环和电流环都采用PI比例积分控制。这种控制策略可以使电机在不同负载情况下都能够快速和稳定地达到给定的转速和电流值。
2.系统仿真结果




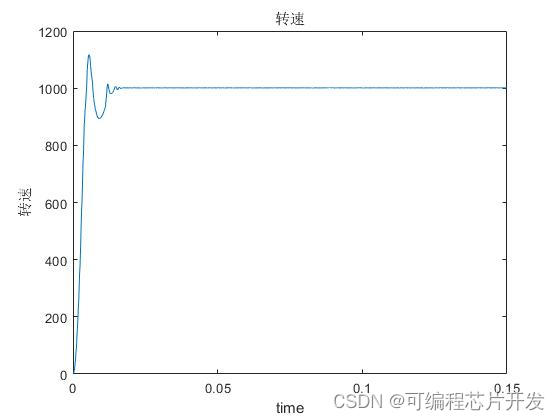
3.核心程序与模型
版本:MATLAB2022a
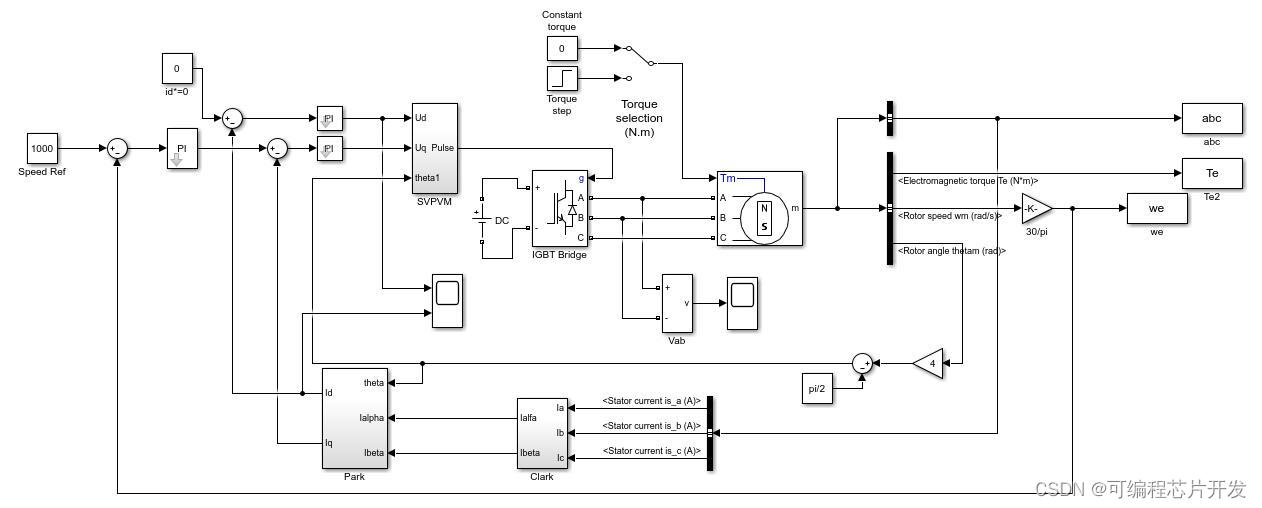
4.系统原理简介
永磁同步电机(PMSM)由于其高效率、高功率密度和优秀的动态性能,在电动汽车、工业自动化等领域得到了广泛应用。为了实现PMSM的高性能控制,通常采用矢量控制策略,并结合空间矢量脉宽调制(SVPWM)技术。而在控制器设计中,双闭环PI(比例-积分)控制器因其结构简单、调整方便、鲁棒性好等优点,被广泛应用于电机控制系统。
4.1 双闭环PI控制器设计
双闭环PI控制器包括速度环和电流环。速度环作为外环,用于控制电机的转速;电流环作为内环,用于控制电机的电流。通过双闭环结构,可以实现对电机转速和电流的精确控制。
速度环PI控制器:速度环PI控制器的输入为参考转速与实际转速的差值,输出为参考交轴电流。
电流环PI控制器:电流环PI控制器包括直轴电流环和交轴电流环。直轴电流环用于控制直轴电流,以实现磁场定向控制;交轴电流环用于控制交轴电流,以实现转矩控制。
4.2 SVPWM技术
SVPWM(空间矢量脉宽调制)技术是一种高效的PWM调制方法,用于将直流电压逆变为三相交流电压。与传统的SPWM(正弦波脉宽调制)相比,SVPWM具有更高的直流电压利用率和更好的动态性能。SVPWM的基本原理是通过合成不同的电压矢量来逼近理想的圆形旋转磁场。在实际应用中,通常采用查表法或实时计算法来实现SVPWM。
4.3 控制系统实现
基于双闭环PI和SVPWM的PMSM控制系统实现过程如下:
采集电机的转速、电流等反馈信息;
根据给定的参考转速和实际转速计算速度误差;
将速度误差输入到速度环PI控制器中计算参考交轴电流;
根据给定的参考直轴电流和实际直轴电流计算直轴电流误差;
将直轴电流误差输入到直轴电流环PI控制器中计算直轴电压参考值;
将参考交轴电流和实际交轴电流输入到交轴电流环PI控制器中计算交轴电压参考值;
根据直轴和交轴的电压参考值进行SVPWM调制生成PWM波形;
将PWM波形作用于逆变器的开关管驱动电机运转;
重复以上步骤实现闭环控制。
5.完整工程文件
v




原装出厂Win10系统镜像)



——23. 变量与函数(一))

)








