字符串下标从 1 开始。
字符串 s 的长度为 n。
" 后缀 i" 代指以第 i 个字符开头的后缀,存储时用 i 代表字符串 s 的后缀 s[i ... n]。
后缀数组(Suffix Array)主要关系到两个数组:sa 和 rk。
后缀数组sa,sa[i] 表示将所有后缀排序后第 i 小的后缀的编号;
排名数组 rk, rk[i] 表示后缀 i 的排名。
这两个数组满足性质:sa[rk[i]]=rk[sa[i]]=i。


/**
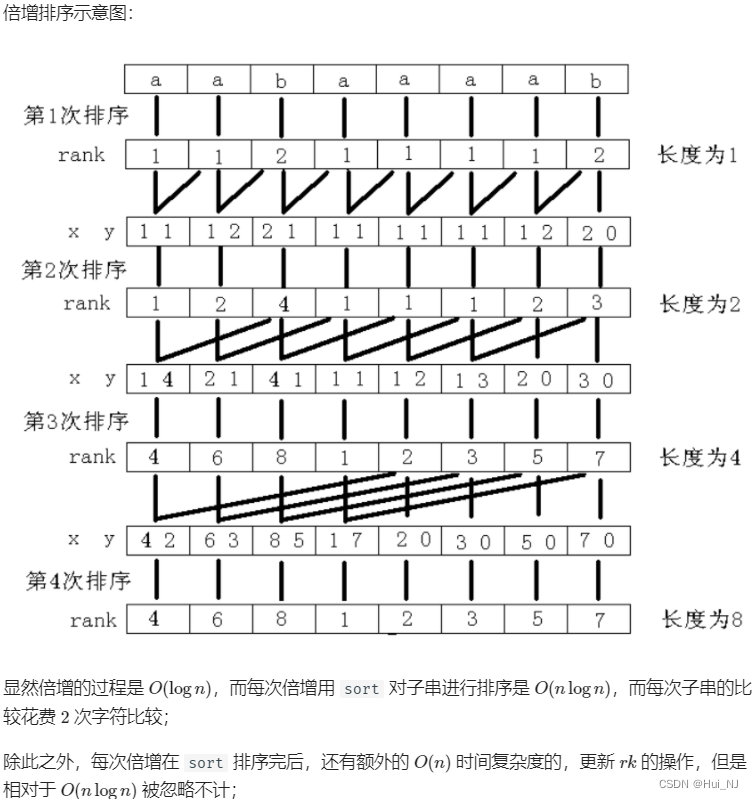
* 倍增的过程是 O(log n),而每次倍增用 sort 对子串进行排序是 O(n\log n),而每次子串的比较花费 2 次字符比较;
* 这个算法的时间复杂度就是 O(n\log^2n)。
*/
// 常规解法, 倍增快速排序
#include <iostream>
#include <string.h>
#include <algorithm>
using namespace std;
const int MAXN = 1000010;
char str[MAXN];
int sa[MAXN]; // 后缀数组sa[i]表示将所有后缀排序后,第i小的后缀的编号
// 为了防止访问 rk[i+k] 导致数组越界,开两倍数组, 省去越界检测,简化程序。
int rk[MAXN << 1]; // 后缀i的排名,常称为排名数组
int oldrk[MAXN << 1];
int k;
int main()
{
cin >> str + 1;
int i = 0, len = strlen(str+1);
// 初始化后缀树组与排名数组
for (i = 1; i <= len; ++i)
{
sa[i] = i;
rk[i] = str[i];
}
// 倍增排序
for (k = 1; k < len; k <<= 1)
{
/**
* 每个后缀子串的次序可以表示为一个二元组(x, y), x表示前半段的次序号,y表示后半段的次序号
* 由于上一次的排序结果已知(即前半段x的排序已知),故只要对后半段进行比较就可以得到当前子串的次序
* 第n次排序表示对每个后缀子串的前1~2^(n-1)个字符进行排序
* 比较二元组(x, x+k) 与 (y, y+k)
* 如果第一关键字相等,则比较第二关键字,关键字小的排名更靠前
*/
sort(sa+1, sa+len+1, [](int x, int y) {
return rk[x] == rk[y] ? rk[x+k] < rk[y+k] : rk[x] < rk[y];
}
);
// 由于计算 rk 的时候, 原来的 rk 会被覆盖,要先复制一份
memcpy(oldrk, rk, sizeof(rk));
int num = 0; // 当前最大的次序号
// 按照sa从小到大给后缀子串更新次序
for (i = 1; i <= len; ++i)
{
// 如果与前一个二元组不相同,则产生新的次序号
if (oldrk[sa[i]] == oldrk[sa[i-1]] && oldrk[sa[i]+k] == oldrk[sa[i-1]+k])
rk[sa[i]] = num;
else
rk[sa[i]] = ++num;
}
cout << "k: " << k << endl;
cout << "sa: ";
for (i = 1; i <= len; ++i)
cout << sa[i] << " ";
cout << endl;
cout << "rk: ";
for (i = 1; i <= len; ++i)
cout << rk[i] << " ";
cout << endl;
}
for (i = 1; i <= len; ++i)
cout << sa[i] << " ";
cout << endl;
return 0;
}
/**
* input:
* aabaaaab
* output:
* k: 1
* sa: 1 4 5 6 2 7 8 3
* rk: 1 2 4 1 1 1 2 3
* k: 2
* sa: 4 5 6 1 7 2 8 3
* rk: 4 6 8 1 2 3 5 7
* k: 4
* sa: 4 5 6 1 7 2 8 3
* rk: 4 6 8 1 2 3 5 7
* 4 5 6 1 7 2 8 3
*/
// 倍增计数排序
/**
* 字符串str的下标从1开始,字符串的长度为len
* "后缀i"代指以第i个字符开头的后缀,存储时用i代表字符串s的后缀s[i...n]
* 后缀数组和排名数组满足: sa[rk[i]] == rk[sa[i]] == i
* 由于计算后缀数组的过程中排序的关键字是排名,值域为 O(n),并且是一个双关键字的排序,可以使用基数排序优化至 O(n)。
*/
#include <iostream>
#include <string.h>
#include <algorithm>
using namespace std;
const int MAXN = 1000010;
char str[MAXN];
int sa[MAXN]; // 后缀数组sa[i]表示将所有后缀排序后,第i小的后缀的编号
// 为了防止访问 rk[i+k] 导致数组越界,开两倍数组, 省去越界检测,简化程序。
int rk[MAXN << 1]; // 后缀i的排名,常称为排名数组
int oldrk[MAXN << 1];
int oldsa[MAXN];
int cnt[MAXN]; // 计数排序用于计数
const int MaxKey = 127; // the maximum value of ASCII is 127
int main()
{
cin >> str + 1;
int i = 0, len = strlen(str+1);
// 统计str中字符的计数分布
for (i = 1; i <= len; ++i)
++cnt[rk[i] = str[i]];
// 统计关键字小于等于i的计数分布
for (i = 1; i <= MaxKey; ++i)
cnt[i] += cnt[i-1];
// 升序计数排序sa
for (i = len; i >= 1; --i)
sa[cnt[rk[i]]--] = i;
memcpy(oldrk+1, rk+1, sizeof(int)*len);
int num = 0; // 当前的最大次序号
// 第一次排序只有一个关键字
for (i = 1; i <= len; ++i)
if (oldrk[sa[i]] == oldrk[sa[i-1]])
rk[sa[i]] = num;
else
rk[sa[i]] = ++num;
for (int k = 1; k < len; k <<= 1)
{
// 对第二关键字:oldsa[i] + k 进行计数排序
memset(cnt, 0, sizeof(cnt));
memcpy(oldsa+1, sa+1, sizeof(int)*len);
for (i = 1; i <= len; ++i)
++cnt[rk[oldsa[i]+k]];
// 首轮排序后,cnt的最大下标不超过len
for (i = 1; i <= len; ++i)
cnt[i] += cnt[i-1];
for (i = len; i >= 1; --i)
sa[cnt[rk[oldsa[i]+k]]--] = oldsa[i];
// 对第一关键字:oldsa[i] 进行计数排序
memset(cnt, 0, sizeof(cnt));
memcpy(oldsa+1, sa+1, sizeof(int)*len);
for (i = 1; i <= len; ++i)
++cnt[rk[oldsa[i]]];
// 首轮排序后,cnt的最大下标不超过len
for (i = 1; i <= len; ++i)
cnt[i] += cnt[i-1];
for (i = len; i >= 1; --i)
sa[cnt[rk[oldsa[i]]]--] = oldsa[i];
memcpy(oldrk+1, rk+1, sizeof(int)*len);
num = 0; // 当前的最大次序号
for (i = 1; i <= len; ++i)
{
// 如果与前一个二元组不相同,则产生新的次序号
if (oldrk[sa[i]] == oldrk[sa[i-1]] && oldrk[sa[i]+k] == oldrk[sa[i-1]+k])
rk[sa[i]] = num;
else
rk[sa[i]] = ++num;
}
}
for (i = 1; i <= len; ++i)
cout << sa[i] << " ";
cout << endl;
return 0;
}
/**
* input:
* aabaaaab
* output:
* 4 5 6 1 7 2 8 3
*/
// 针对大数据做性能优化
/**
* https://www.luogu.com.cn/problem/P3809
* 字符串str的下标从1开始,字符串的长度为len
* "后缀i"代指以第i个字符开头的后缀,存储时用i代表字符串s的后缀s[i...n]
* 后缀数组和排名数组满足: sa[rk[i]] == rk[sa[i]] == i
* 由于计算后缀数组的过程中排序的关键字是排名,值域为 O(n),并且是一个双关键字的排序,可以使用基数排序优化至 O(n)。
* 针对大数据进行优化
*/
#include <iostream>
#include <string.h>
#include <algorithm>
using namespace std;
const int MAXN = 1000010;
char str[MAXN];
int sa[MAXN]; // 后缀数组sa[i]表示将所有后缀排序后,第i小的后缀的编号
// 为了防止访问 rk[i+k] 导致数组越界,开两倍数组, 省去越界检测,简化程序。
int rk[MAXN]; // 后缀i的排名,常称为排名数组
int oldrk[MAXN << 1];
int key1[MAXN]; // key1[i] = rk[oldsa[i]](作为基数排序的第一关键字数组)
int oldsa[MAXN];
int cnt[MAXN]; // 计数排序用于计数
/**
* 用函数 cmp 来计算是否重复
* 同样是减少不连续内存访问,在数据范围较大时效果比较明显。
*/
bool cmp(int x, int y, int k)
{
return oldrk[x] == oldrk[y] && oldrk[x + k] == oldrk[y + k];
}
int main()
{
cin >> str + 1;
int i = 0, len = strlen(str+1);
int MaxKey = 127; // the maximum value of ASCII is 127
// 统计str中字符的计数分布
for (i = 1; i <= len; ++i)
++cnt[rk[i] = str[i]];
// 统计关键字小于等于i的计数分布
for (i = 1; i <= MaxKey; ++i)
cnt[i] += cnt[i-1];
// 升序计数排序sa
for (i = len; i >= 1; --i)
sa[cnt[rk[i]]--] = i;
int num = 0; // 最大次序号
/**
* m=num 就是优化计数排序值域
* 每次对 rk 进行更新之后,我们都计算了一个 num,这个 num 即是 rk 的值域,将值域改成它即可。
*/
for (int k = 1 ;; k <<= 1, MaxKey = num)
{
/**
* 第二关键字无需计数排序, 第二关键字排序的实质,
* 其实就是把超出字符串范围(即 sa[i] + k > len)的 sa[i] 放到 sa 数组头部,然后把剩下的依原顺序放入
*/
for (num = 0, i = len; i > len - k; --i)
oldsa[++num] = i;
for (i = 1; i <= len; ++i)
if (sa[i] > k)
oldsa[++num] = sa[i] - k;
/**
* 对第一关键字:oldsa[i] 进行计数排序
* 将 rk[oldsa[i]] 存下来,减少不连续内存访问, 这个优化在数据范围较大时效果非常明显。
*/
memset(cnt, 0, sizeof(cnt));
for (i = 1; i <= len; ++i)
++cnt[key1[i] = rk[oldsa[i]]];
for (i = 1; i <= MaxKey; ++i)
cnt[i] += cnt[i-1];
for (i = len; i >= 1; --i)
sa[cnt[key1[i]]--] = oldsa[i];
memcpy(oldrk+1, rk+1, sizeof(int)*len);
num = 0; // 当前的最大次序号
for (i = 1; i <= len; ++i)
{
// 如果与前一个二元组不相同,则产生新的次序号
rk[sa[i]] = cmp(sa[i], sa[i - 1], k) ? num : ++num;
}
// 若其值域为 [1,n] 那么每个排名都不同,此时无需再排序
if (num == len)
break;
}
for (i = 1; i <= len; ++i)
cout << sa[i] << " ";
cout << endl;
return 0;
}
/**
* input:
* aabaaaab
* output:
* 4 5 6 1 7 2 8 3
*/
)












先来认识GTM架构)



![[2024区块链开发入门指引] - 比特币运行原理](http://pic.xiahunao.cn/[2024区块链开发入门指引] - 比特币运行原理)
)
