Attention机制

前置知识：RNN，LSTM/GRU

提出背景

Attention模型是基于Encoder-Decoder框架提出的。Encoder-Decoder框架，也就是编码-解码框架，主要被用来处理序列-序列问题。

Encoder：编码器，将输入的序列<x1,x2,x3…xn>编码，使其转化为一个语义编码C，这个C中就储存了序列<x1,x2,x3…xn>的信息。

Decoder：解码器，根据输入的语义编码C，然后将其解码成序列数据

编码方式有很多种，在文本处理领域主要有RNN、LSTM、GRU、BiRNN、BiLSTM、BiGRU等。解码方式主要有两种：

[论文1]Cho et al., 2014 . Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation.
[论文2]Sutskever et al., 2014. Sequence to Sequence Learning with Neural Networks.

论文1中指出，因为语义编码C包含了整个输入序列的信息，所以在解码的每一步都引入C。文中Ecoder-Decoder均是使用RNN，在计算每一时刻的输出yt时，都应该输入语义编码C，即ht=f(ht-1,yt-1,C)，p(yt)=f(ht,yt−1,C)。

$y_1=f(C) \\y_2=f(C,y_1) \\y_3=f(C,y_1,y_2)$

问题在于：语义编码C是由输入序列X的每个单词经过Encoder 编码产生的，这意味着不论是生成哪个单词，y1,y2还是y3，其实输入序列X中任意单词对生成某个目标单词yi来说影响力都是相同的（其实如果Encoder是RNN的话，理论上越是后输入的单词影响越大，并非等权）

论文2中的方式相对简单，只在Decoder的初始输入引入语义编码C，将语义编码C作为隐藏层状态值h0的初始值，p(yt)=f(ht,yt−1)。

问题在于：将整个序列的信息压缩在了一个语义编码C中，用一个语义编码C来记录整个序列的信息，如果序列是长序列，那么只用一个语义编码C来表示整个序列的信息肯定会产生大量损失，且容易出现梯度消失的问题。

Attention原理

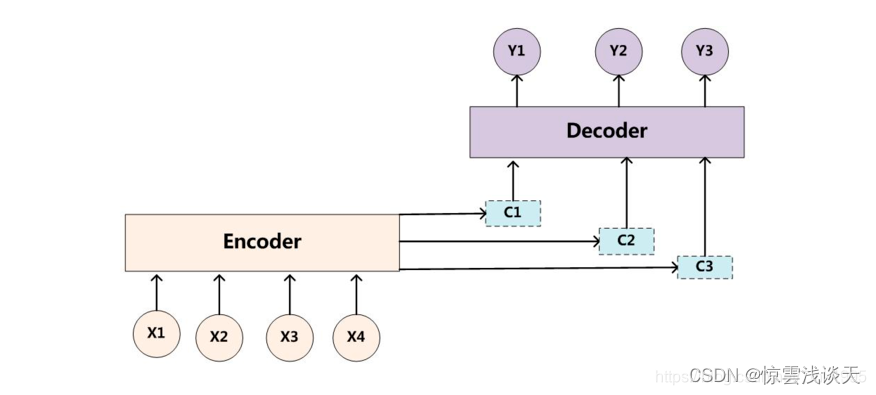
当一个语义编码C无法有效解决问题时，就尝试引入多个C。对于不同的预测Yi，注意力会集中在不同的C上，即由固定的中间语义C换成了根据当前输出单词来调整为加入注意力模型变化的Ci。

Yi是Decoder的当前输出单词，Ci是Decoder的当前注意力向量。Ci是根据Decoder的上一时刻的输出单词Yi-1和隐藏层Si-1计算出来的，它表示了Decoder对Encoder的输入序列的不同部分的关注程度。

在下文中，H和S都表示RNN隐藏层的值，H表示Encoder的第i个隐藏层的值，S表示Decoder的第i个隐藏层的值。

Yi是根据Ci和Si-1生成的，它表示了Decoder根据注意力向量选择合适的输入单词进行翻译的结果。

Si是根据Decoder的第i-1个隐藏层的值Si-1和第i-1个输出单词Yi-1计算出来的。具体的计算方法取决于Decoder使用的RNN的类型，比如LSTM或GRU。

为了体现出输入序列中不同单词对当前预测的影响程度不同，对于每一个预测输出Yi，Attention模型中都会给出一个概率分布：

$(X_j,p_j)$

其中，f(xj)即为对应隐藏层的值hj，用αi=[αi1,αi2,…,αin]表示注意力分配概率向量，即αij=pj，使得：

$C_i=\sum\limits_{j=1}^n\alpha_{ij}h_j$

在Attention机制中，Decoder的每个隐藏层Si都会与Encoder的所有隐藏层Hi进行相关性计算，得到一个注意力分配概率分布αi。然后，根据这个概率分布，对Encoder的隐藏层H进行加权求和，得到一个注意力向量Ci。这个向量就是Decoder的当前输出Yi所关注的Encoder的输入序列的语义表示。

求得语义编码Ci的关键在于计算Attention模型所需要的输入句子的单词注意力分配概率值，即α。

Decoder上一时刻的输出值Yi-1与上一时刻传入的隐藏层的值Si-1通过RNN生成Si，然后计算Hi与h1，h2，h3…hm的相关性，得到相关性评分[f1,f2,f3…fm]，然后对fj使用softmax激活就得到注意力分配αij。

此处使用的是Soft Attention，所有的数据都会注意，并计算出相应的注意力权值，不会设置筛选条件。

还有一种Hard Attention会在生成注意力权重后筛选掉一部分不符合条件的注意力，让它的注意力权值为0。

Attention机制本质思想

事实上，Attention机制并非一定基于Encoder-Decoder框架。

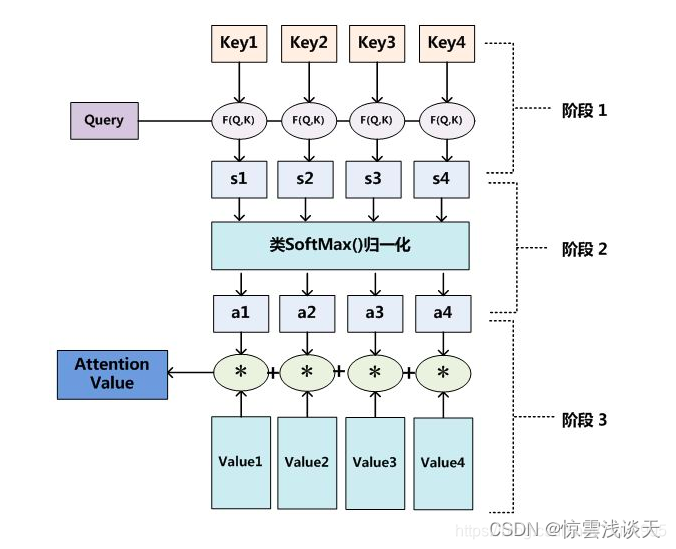
将Source中的构成元素想象成是由一系列的<Key,Value>数据对构成，此时给定Target中的某个元素Query，通过计算Query和各个Key的相似性或者相关性，得到每个Key对应Value的权重系数再加权求和即可得最终的Attention Value。

$Attention(query,source)=\sum\limits^{L_x}_{i=1}a_i*value_i \\a_i=f(\rho_i) \\\rho_i=\rho(query,key_i)$

Lx表示source的长度，ρ(q,ki)的计算如下：

内积： $\rho(q,k_i)=q·k_i$

Cosine相似性： $\rho(q,k_i)=\frac{q·k_i}{\parallel q \parallel·\parallel k_i \parallel}$

MLP网络： $\rho(q,k_i)=MLP(q,k_i)$

内积：Transformer使用的方法
Cosine相似性-余弦相似度：分子为点积，分母为向量的L2范数（各元素平方和的平方根）
MLP网络不常用

在得到相关性ρ之后，引入激活函数（如softmax），对相关性归一化，即将原始计算分值整理成所有元素权重之和为1的概率分布，同时利用激活函数的内在机制突出重要元素的权重。

$a_i=softmax(\rho_i)=\frac{e^{p_i}}{\sum^{L_x}_{j=1}e^{\rho_j}}$

Attention机制总结

相关性分析
归一化
加权求和

缺点

只能在Decoder阶段实现并行运算，Encoder部分依旧采用的是RNN、LSTM等顺序编码的模型，Encoder部分依然无法实现并行运算。
Encoder部分目前仍旧依赖于RNN，对于长距离的两个词相互之间的关系没有办法很好的获取。

改进：Self-Attention

在一般任务的Encoder-Decoder框架中，输入Source和输出Target内容是不一样的，比如对于英-中机器翻译来说，Source是英文句子，Target是对应的翻译出的中文句子，Attention机制发生在Target的元素和Source中的所有元素之间。

Self-Attention是在Source内部元素或者Target内部元素之间发生的Attention机制，也可以理解为Target=Source这种特殊情况下的注意力计算机制，相当于是Query=Key=Value，计算过程与Attention一样。

引入Self-Attention后会更容易捕获句子中长距离的相互依赖的特征，Self-Attention在计算过程中会直接将句子中任意两个单词的联系通过一个计算步骤直接联系起来，所以远距离依赖特征之间的距离被极大缩短，有利于有效地利用这些特征。除此外，Self Attention对于增加计算的并行性也有直接帮助作用。正好弥补了attention机制的两个缺点，这就是为何Self Attention逐渐被广泛使用的主要原因。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/590756.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！