数据结构大作业,基于图论中的最小生成树的图像分割。一个很古老的算法,精度远远不如深度学习算法,但是对于代码能力是一个很好的锻炼。
课设要求:
( 1 )输入:图像(例如教室场景图);
( 2 )使用基于基于图论、像素聚类和深度语义这三大类方法之一实现图像分割;
( 3 )输出: 展示原始图像和分割结果图,定义并展示分割指标判定分割好坏。
实现环境:python Numpy+PyQt5交互界面实现
参考文献 Efficient Graph-Based Image Segmentation | International Journal of Computer VisionThis paper addresses the problem of segmenting an image into regions. We define a predicate for measuring the evidence for a boundary between two regions u https://link.springer.com/article/10.1023/B:VISI.0000022288.19776.77
https://link.springer.com/article/10.1023/B:VISI.0000022288.19776.77
基于图论中的最小生成树的图像分割原理如下:
1. 模型构建
像素点:由图像的小方格组成的,这些小方块都有一个明确的位置和被分配的色彩数值,小方格颜色和 位置就决定该图像所呈现出来的样子。 颜色值:常用的颜色空间有 RGB、HSV 等,RGB 是我们接触最多的颜色空间,以 RGB 空间为例,由三个通道表示一幅图像,分别为红色(R),绿色(G)和蓝色(B)。这三种颜色的不同组合可以形成几乎所有的其它颜色。
要将图像数据转化为可用于图像分割的无向图数据结构,需要构建以下映射关系:
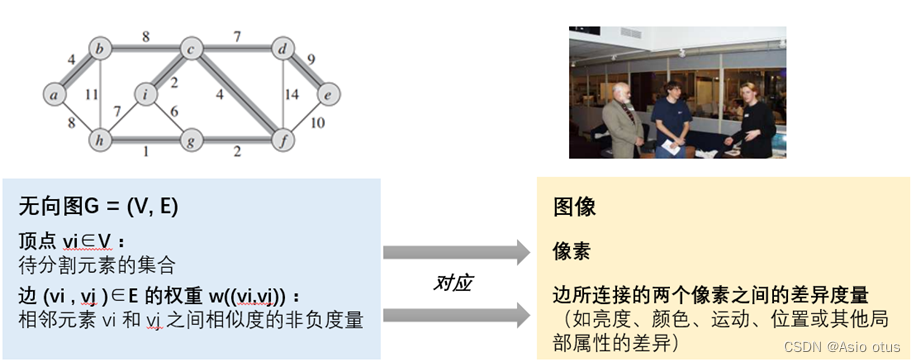
设假设 G = (V, E) 是一个无向图, 图像中的每个像素可以视为 图中的一个顶点,所有顶点 vi∈V 构成待分割顶点的集合,即未分割的图像。图像中两个相邻像素所对应的顶点vi,vj之间存在一条边 (vi , vj )∈E。边 (vi , vj )∈ E的所携带的权重 w((vi,vj)) 信息,即是该边所连接的相邻像素点 vi,vj之间的差异度量(如亮度、颜色、运动、位置或其他局部属性的差异)。基于图的图像分割的目标,既是将顶点集合 V 分割为多个分量(即区域)S,每个分量都对应图 G = (V, E ) 中的一个连通分量。判断顶点属于哪一分量的标准应当来自于顶点所连接的边的权重,同一区域中两个顶点之间的边应该具有相对较低的权重,而不同区域中顶点之间的边应该具有较高的权重。
2. 区域划分原理
在最开始的时候,每个像素点都是相互独立的,每个像素点都属于一个区域。根据最小生成树的原理, 在每次选择一条权重大于阈值的边之后,就会使得两个顶点所在的两个区域连通。在遍历完所有边之后,图 中就会形成若干个最小生成树,每一个最小生成树连通的顶点都属于同一个区域。 构建和划分过程如下图:
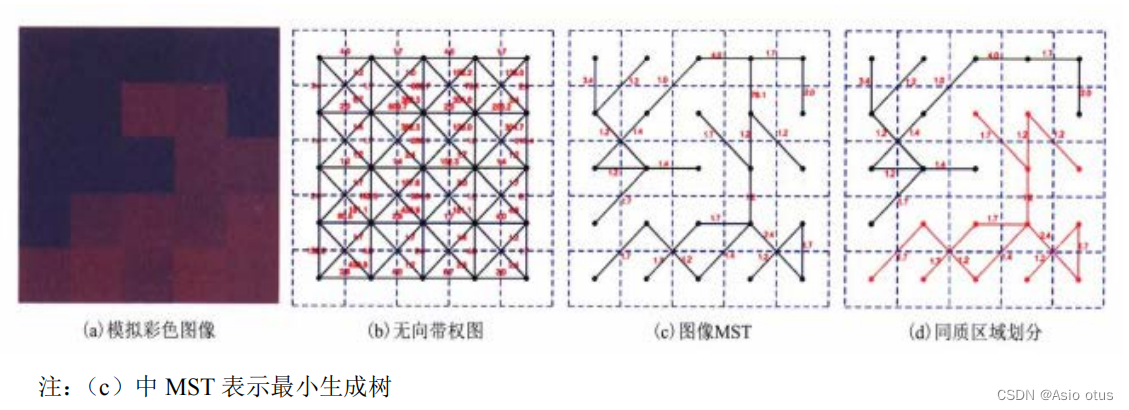
除此之外,最后可能还有若干个点或者较小的区域存在。这些区域往往是噪声点,需要将这些区域合并 到相邻的大区域,或者在最开始的时候对图像进行去噪处理。
算法流程
- 构建图:将图像中的像素表示为图的节点,并根据像素之间的相似性连接节点,形成图的边。常用的相似性度量包括颜色、纹理和空间距离等。
- 定义代价函数:根据图的节点和边的属性定义一个代价函数,该函数用于评估将图像分割为不同区域的代价。代价函数通常考虑区域内像素之间的相似性和区域之间的差异性。
- 优化过程:使用优化算法(如最小割和最大流算法)来最小化代价函数,从而得到最优的图像分割结果。优化过程通常涉及对图的节点和边进行切割,以使得代价函数最小化。
- 区域合并:在得到初步的图像分割结果后,可能会进行一系列的合并操作,以进一步提高分割的质量。合并操作通常基于一些合并准则,如区域相似性和区域大小等
代码下载链接:数据结构大作业基于图论的图像分割python+PyQt5交互界面资源-CSDN文库
)
C卷 (JavaPythonNode.jsC++))

(A-F))




-ARM Neon详细介绍)
)
![三、Mysql安全性操作[用户创建、权限分配]](http://pic.xiahunao.cn/三、Mysql安全性操作[用户创建、权限分配])


)





