PPO 近端策略优化算法
- PPO = 概率比率裁剪 + 演员-评论家算法
- 演员-评论家算法:多智能体强化学习核心框架
- 概率比率裁剪:逐步进行变化的方法
- PPO 目标函数的设计
- 重要性采样
- KL散度
PPO = 概率比率裁剪 + 演员-评论家算法
论文链接:https://arxiv.org/abs/1707.06347
OpenAI 提出 PPO 旨在解决一些在策略梯度方法中常见的问题,特别是与训练稳定性和样本效率有关的问题。
能在提高学习效率和保持训练稳定性之间找到平衡。
策略梯度方法的问题:
-
策略更新过快:
在传统的策略梯度方法中,如果每次更新都大幅度改变策略,可能会导致学习过程变得非常不稳定。
这种大幅更新可能会使得智能体忘记之前有效的策略,或者探索到低效的行为区域。 -
数据利用率低:
许多强化学习算法,特别是那些基于样本的算法,需要大量的数据才能学到有效的策略。
PPO试图通过更有效地使用数据来缓解这个问题,使得从每个数据样本中学到更多信息。 -
训练周期长:
由于数据利用率低,传统的强化学习算法通常需要很长的训练周期才能收敛到一个好的策略。
PPO通过改进学习算法来减少所需的训练时间。
PPO算法在演员-评论家的框架基础上,使用了 概率比率裁剪 技巧来控制策略更新的幅度,以确保训练的稳定性和性能。
演员-评论家算法:多智能体强化学习核心框架
请猛击:演员-评论家算法:多智能体强化学习核心框架
概率比率裁剪:逐步进行变化的方法
想象你有两个不同的蛋糕配方,这个比率就像是告诉你,使用新配方做蛋糕的可能性与旧配方相比有多大的变化。
如果我们的新策略和旧策略差别太大,那就像是突然完全改变蛋糕的配方,可能会做出一个很不一样的蛋糕,我们不确定它会好吃,还是不好吃。
所以,PPO通过计算概率比率来确保新策略不会偏离旧策略太远。
在每次策略更新时,它计算新策略和旧策略之间的比率,并通过限制这个比率的大小来裁剪更新幅度,以防止过大的改变。
解决如何安全地逐步进行变化,控制变化的方法。
具体请见目标函数的设计。
PPO 目标函数的设计
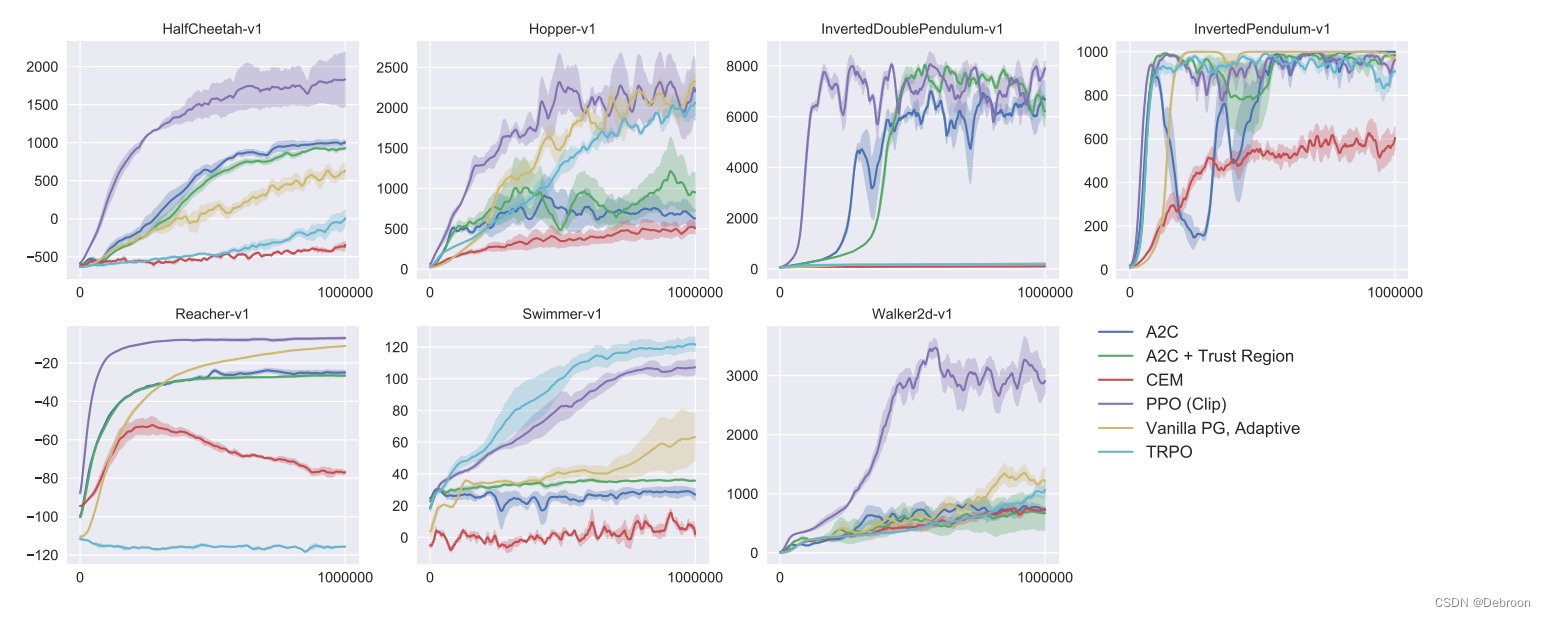
在测试中,PPO 基本在每个任务都是第一梯队。
那我们说一下 PPO 到底做了什么,居然比 A2C (另一种演员-评论家的改进算法)还要好。
近端,主要体现在其目标函数的设计上。
在PPO(近端策略优化)算法中,结合使用重要性采样和KL散度实现了主要的目标。
重要性采样:
- 探索与利用的平衡:重要性采样帮助算法判断新策略(新动作)与旧策略(旧动作)相比的效果。如果新策略比旧的好,算法会更倾向于采用新策略(这是“利用”)。但同时,算法也会尝试一些不同的策略(这是“探索”),以找到可能更好的解决方案。
- 渐进式更新:通过重要性采样,PPO能够逐渐、小心地改进策略,而不是一次性做出巨大的改变。这样的逐步改进有助于算法稳定地学习和适应新策略。
KL散度:
- 防止过度探索:KL散度用于确保新策略不会偏离旧策略太远。这个约束防止了算法在探索新策略时过度激进,从而避免了可能导致性能下降的大幅度策略变动。
- 维持学习的稳定性:通过限制新旧策略之间的差异,KL散度有助于保持学习过程的稳定性。这种稳定性对于复杂的学习任务特别重要,因为它减少了学习过程中的不确定性和波动。
重要性采样
你正在玩一个跳舞游戏。
在这个游戏里,你有一系列的舞蹈动作可以选择。
刚开始时,你只会一些基础的动作(这是你的“旧策略”)。
现在,你学会了一些新的、酷炫的舞蹈动作(这是你的“新策略”)。
在这个游戏里,你想要知道这些新动作是否真的比旧的好。
但是,你不能一次就完全改变你的舞蹈风格,因为这样你可能会跳得很差。
所以,你需要一种方法来慢慢地、安全地加入新动作。
使用重要性采样,你可以基于旧动作的经验来估计新动作的效果。
比如,如果新动作只是在旧动作的基础上做了一些小改动(比如多举了一下手),你可以推测这个新动作会有类似的效果。
通过比较,你可以决定哪些新动作真的相似,值得加入到你的舞蹈里,同时确保你的整体舞蹈还是很流畅。
不仅链接了新旧动作,还是渐进式更新。
在这个过程中,你不需要每次都完全重新学习动作。
相反,你只是在旧动作的基础上做一些小的调整。
这样,你可以逐渐地、稳步地改进你的动作,而不是一下子完全改变。
KL散度
你的舞蹈老师给了你一个规则:虽然可以尝试新动作,但是不能让你的舞蹈风格变化太大,否则会失去控制,可能跳得一团糟。
KL散度就像是舞蹈老师的一条规则,它告诉你新舞蹈和旧舞蹈之间的差别。
如果差别太大,就意味着你可能偏离了舞蹈的基本风格太远,需要调整一下。
这样,你就可以在尝试新动作的同时,保持你的舞蹈整体风格和质量。
仅仅使用重要性采样可能会导致策略变化过大,特别是在新策略与旧策略差异显著时。
KL散度提供了一种衡量策略之间差异的方法。
通过限制新旧策略之间的KL散度,PPO能够保证学习过程的连续性和平滑性,减少策略更新的剧烈波动。
数学公式:
- J P P O θ ′ ( θ ) = J θ ′ ( θ ) − β K L ( θ , θ ′ ) ⏟ Regularization = E ( s t , a t ) ∼ π θ ′ [ p θ ( a t ∣ s t ) p θ ′ ( a t ∣ s t ) A θ ′ ( s t , a t ) ] − β K L ( θ , θ ′ ) \begin{aligned} J_{\mathrm{PPO}}^{\theta^{\prime}}(\theta)& =J^{\theta^{\prime}}(\theta)-\underbrace{\beta\mathrm{KL}(\theta,\theta^{\prime})}_{\text{Regularization}} \\ &=\mathbb{E}_{(s_t,a_t)\sim\pi_{\theta^{\prime}}}\left[\frac{p_\theta\left(a_t\mid s_t\right)}{p_{\theta^{\prime}}\left(a_t\mid s_t\right)}A^{\theta^{\prime}}\left(s_t,a_t\right)\right]-\beta\mathrm{KL}(\theta,\theta^{\prime}) \end{aligned} JPPOθ′(θ)=Jθ′(θ)−Regularization βKL(θ,θ′)=E(st,at)∼πθ′[pθ′(at∣st)pθ(at∣st)Aθ′(st,at)]−βKL(θ,θ′)
这个公式是近端策略优化(PPO)算法中的一个重要部分,它包含了重要性采样和KL散度。
-
重要性采样:
- 公式的这部分: p θ ( a t ∣ s t ) p θ ′ ( a t ∣ s t ) \frac{p_\theta(a_t | s_t)}{p_{\theta'}(a_t | s_t)} pθ′(at∣st)pθ(at∣st),表示的是重要性采样比率。
- 这里, p θ ′ ( a t ∣ s t ) p_{\theta'}(a_t | s_t) pθ′(at∣st) 是旧策略(即上一次更新前的策略)在状态(s_t)下选择动作(a_t)的概率。
- p θ ( a t ∣ s t ) p_\theta(a_t | s_t) pθ(at∣st) 是新策略(即当前更新的策略)在相同状态下选择同一动作的概率。
- 通过这个比率,我们可以量化新旧策略之间在选择特定动作上的差异。
-
优势函数 A θ ′ ( s t , a t ) A^{\theta'}(s_t, a_t) Aθ′(st,at):
- 公式中的 A θ ′ ( s t , a t ) A^{\theta'}(s_t, a_t) Aθ′(st,at) 是优势函数,它评估在特定状态下采取某个动作相对于平均情况的好坏。
- 优势函数用于量化一个特定动作比平均情况要好或坏多少。
-
期望值 E \mathbb{E} E:
- E ( s t , a t ) ∼ π θ ′ [ … ] \mathbb{E}_{(s_t,a_t)\sim\pi_{\theta'}}[…] E(st,at)∼πθ′[…] 表示对于由旧策略 π θ ′ \pi_{\theta'} πθ′ 生成的状态和动作的期望值。
- 这意味着我们在计算这个公式时,考虑的是在旧策略下可能发生的所有状态和动作组合。
-
KL散度:
- 公式中的 K L ( θ , θ ′ ) \mathrm{KL}(\theta, \theta') KL(θ,θ′) 代表KL散度,它是一种衡量两个概率分布差异的方法。
- 在这里,它用来衡量新策略和旧策略之间的差异。
- β \beta β是一个调节参数,它控制了我们对策略变化的惩罚强度。KL散度越大,意味着新旧策略差异越大。
-
整体公式:
- 整个公式的第一部分, E ( s t , a t ) ∼ π θ ′ [ … ] \mathbb{E}_{(s_t,a_t)\sim\pi_{\theta'}}[…] E(st,at)∼πθ′[…],计算的是在旧策略下,采用新策略能带来多少优势。
- 第二部分, − β K L ( θ , θ ′ ) -\beta\mathrm{KL}(\theta, \theta') −βKL(θ,θ′),则是在控制新策略不要偏离旧策略太远的约束。
所以,这个公式基本上是在做两件事:
- 一方面,它试图找到一个新策略,使得在旧策略下的表现更好;
- 另一方面,它确保新策略不会与旧策略差异太大,从而保持学习的稳定性。










)







)
