前置知识

二叉树节点的定义

• 二叉树是递归定义的

/*** Definition for a binary tree node.（LeetCode）*/public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val = val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}

广度优先遍历搜索 Breath First Search (BFS)

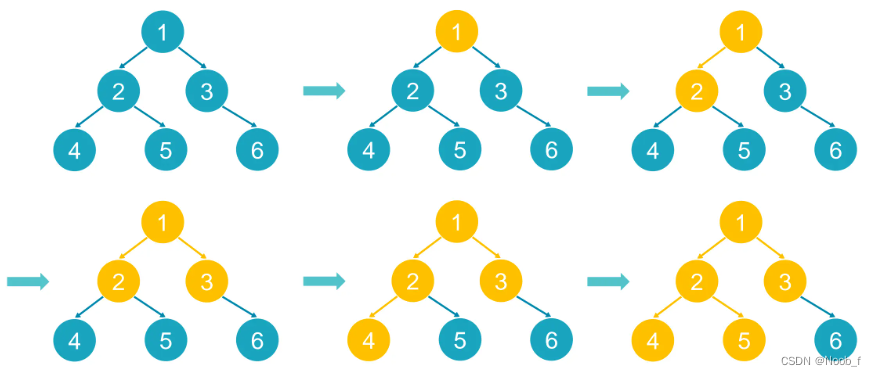
• BFS通常需要使用一个队列来维护搜索过程。
• 先进先出 First In First Out (FIFO)。

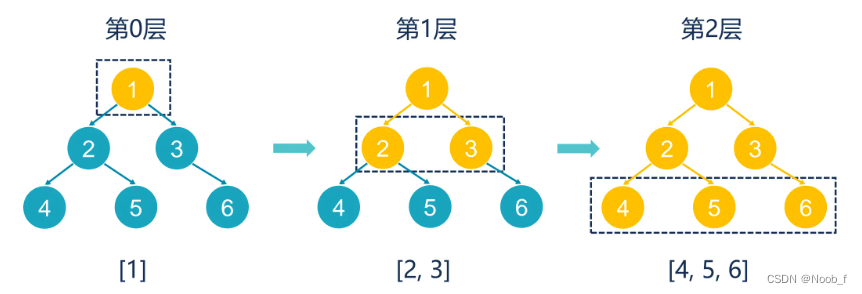
层序遍历 Level-order Traverse

• 树的广度优先遍历亦可称为层序遍历。
• 从上到下、从左到右访问树中的节点，每一层的节点都按顺序出现。
  

多源BFS

单源BFS：从某一个点开始（一个起点）。
多源BFS：从多个点同时开始走（多个起点）。

二叉树结构

LeetCode 2236. 判断根结点是否等于子结点之和

• 比较二叉树根节点的值val、左子树left和右子树right节点的值之和

class Solution {public boolean checkTree(TreeNode root) {if( root.val == root.left.val + root.right.val )return true;elsereturn false;}
}

二叉树的层序遍历

LeetCode 102. 二叉树的层序遍历

• 时间复杂度O(n)
• 空间复杂度O(n)

class Solution {public List<List<Integer>> levelOrder(TreeNode root) {// 遍历结果，注意题目输出格式List<List<Integer>> traverseResult  = new LinkedList<>();// 根节点为空的情况if ( root == null )return traverseResult;// BFS，使用队列Queue<TreeNode> queue = new LinkedList<>();// 前面判断了根节点为空，这里根节点入队列queue.add(root);// 借助队列层序遍历二叉树，直到所有节点出列while( !queue.isEmpty() ) {// 每层节点个数int levelCount = queue.size();// 该层每个节点值List<Integer> levelResult = new ArrayList<>();// 遍历该层节点for (int i=0; i<levelCount; i++) {// 队头节点出队列TreeNode node = queue.poll();// 出列节点值，加入List集合levelResult.add(node.val);// 左节点存在，入队if ( node.left != null ) {queue.add( node.left );}// 右节点存在，入队if ( node.right != null ) {queue.add( node.right );}}// 该层遍历结果traverseResult.add( levelResult );}return traverseResult;}
}

LeetCode 107. 二叉树的层序遍历 II

• BFS层序遍历，在遍历完一层节点之后，将存储该层节点值的列表添加到结果列表的头部。
• 时间复杂度O(n)
• 空间复杂度O(n)

class Solution {public List<List<Integer>> levelOrderBottom(TreeNode root) {// 遍历结果，注意题目输出格式、自底向上List<List<Integer>> traverseResult = new LinkedList<>();// 根节点为空的情况if ( root == null )return traverseResult;// BFS，使用队列Queue<TreeNode> queue = new LinkedList<>();// 前面判断了根节点为空，这里根节点入队列queue.add(root);// 借助队列层序遍历二叉树，直到所有节点出列while( !queue.isEmpty() ) {// 每层节点个数int levelCount = queue.size();// 该层每个节点值List<Integer> levelResult = new ArrayList<>();// 遍历该层节点for ( int i=0; i<levelCount; i++ ) {// 队头节点出队列TreeNode node = queue.poll();// 出列节点值，加入List集合levelResult.add(node.val);// 左节点存在，入队if ( node.left != null )queue.add(node.left);// 右节点存在，入队if ( node.right != null )queue.add(node.right);}// 该层遍历结果，将存储该层节点值的列表添加到结果列表的头部。traverseResult.add(0,levelResult);}return traverseResult;}
}

LeetCode 103. 二叉树的锯齿形层序遍历

• BFS层序遍历，利用双端队列交替顺序输出每层结果。
• 时间复杂度O(n)
• 空间复杂度O(n)

class Solution {public List<List<Integer>> zigzagLevelOrder(TreeNode root) {List<List<Integer>> traverseResult = new LinkedList<>();if ( root == null )return traverseResult;// BFS层序遍历，双端队列实现输出顺序交替Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);// true时从左往右，false时从右往左boolean flag = true;while( !queue.isEmpty() ) {int levelCount = queue.size();// 双端队列LinkedList<Integer> levelResult = new LinkedList<>();for(int i=0; i<levelCount; i++) {TreeNode node = queue.poll();// 从左往右，插入双端队列末尾if(flag)levelResult.offerLast(node.val);// 从右往左，插入双端队列头部elselevelResult.offerFirst(node.val);if ( node.left != null)queue.offer(node.left);if ( node.right != null )queue.offer(node.right);}traverseResult.add(levelResult);// 每层遍历完，修改标记flag = !flag;}return traverseResult;}
}

LeetCode 637. 二叉树的层平均值

• BFS，层平均值 = 每层节点值之和 / 每层节点数量
• 时间复杂度O(n)
• 空间复杂度O(n)

class Solution {public List<Double> averageOfLevels(TreeNode root) {List<Double> avgResult = new ArrayList<>();Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while( !queue.isEmpty() ) {int levelCount = queue.size();double levelSum = 0;for(int i=0; i<levelCount; i++) {TreeNode node = queue.poll();levelSum += node.val;if ( node.left != null )queue.offer(node.left);if ( node.right != null )queue.offer(node.right);}avgResult.add( levelSum / levelCount );}return avgResult;}
}

LeetCode 199. 二叉树的右视图

• BFS，记录下每层的最后一个元素。
• 时间复杂度O(n)
• 空间复杂度O(n)

class Solution {public List<Integer> rightSideView(TreeNode root) {List<Integer> rightResult = new ArrayList<>();if ( root == null )return rightResult;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while ( !queue.isEmpty() ) {int levelCount = queue.size();for(int i=0; i<levelCount; i++) {TreeNode node = queue.poll();// 每层最右侧节点if ( node.left != null )queue.offer(node.left);if ( node.right != null )queue.offer(node.right);if (i+1 == levelCount)rightResult.add(node.val);}}return rightResult;}
}

LeetCode 513. 找树左下角的值

• BFS层序遍历，最后更新的值，是最后一层最左节点值。
• 注意节点值的数据范围，$$-2^{31}<=Node.val<=2^{31}-1$$
• 时间复杂度O(n)
• 空间复杂度O(n)

class Solution {public int findBottomLeftValue(TreeNode root) {Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);int bottomLeft = root.val;while ( !queue.isEmpty() ) {int levelCount = queue.size();for(int i=0; i<levelCount; i++) {TreeNode node = queue.poll();// 每层最左边节点的值if ( i == 0 )bottomLeft = node.val;if ( node.left != null )queue.offer(node.left);if ( node.right != null )queue.offer(node.right);}}// 层序遍历，bottomLeft是最后一层最左边节点的值return bottomLeft;}
}

LeetCode 515. 在每个树行中找最大值

• BFS层序遍历，取每层全部节点中的最大值。
• 注意节点值的数据范围，$$-2^{31}<=Node.val<=2^{31}-1$$
• 时间复杂度O(n)
• 空间复杂度O(n)

class Solution {public List<Integer> largestValues(TreeNode root) {List<Integer> largestResult = new LinkedList<>();if ( root == null )return largestResult;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while ( !queue.isEmpty() ) {int levelCount = queue.size();int maxValue = Integer.MIN_VALUE;for(int i=0; i<levelCount; i++) {TreeNode node = queue.poll();if ( maxValue < node.val )maxValue = node.val;if ( node.left != null )queue.offer(node.left);if ( node.right != null )queue.offer(node.right);}largestResult.add(maxValue);}return largestResult;}
}

LeetCode 1161. 最大层内元素和

• BFS层序遍历，累加每层元素之和，记录和最大的层号。
• 注意节点值的数据范围，$$-10^5<=Node.val<=10^5$$
• 注意变量赋值位置，是否受循环影响（代码思路没错，卡在这个细节好久，最后发现是这里的问题）
• 时间复杂度O(n)
• 空间复杂度O(n)

class Solution {public int maxLevelSum(TreeNode root) {int maxLevel = 1;int maxSum = Integer.MIN_VALUE;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);int level = 1;while ( !queue.isEmpty() ) {int levelCount = queue.size();int levelSum = 0;for(int i=0; i<levelCount; i++) {TreeNode node = queue.poll();levelSum += node.val;if ( node.left != null )queue.offer(node.left);if ( node.right != null )queue.offer(node.right);}if ( levelSum > maxSum ) {maxLevel = level;maxSum = levelSum;}level += 1;}return maxLevel;}
}

LeetCode 101. 对称二叉树

• 更适合用深度优先遍历搜索DFS解这道题。
• BFS层序遍历，每层从左往右、从右往左的结果是否相等。
• 注意空节点缺省值填充。
• 注意节点值的数据范围，$$-100<=Node.val<=100$$
• 时间复杂度O(n)
• 空间复杂度O(n)

class Solution {public boolean isSymmetric(TreeNode root) {// BFS做法if ( root == null )return true;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while( !queue.isEmpty() ) {int levelCount = queue.size();LinkedList<Integer> leftResult = new LinkedList<>();LinkedList<Integer> rightResult = new LinkedList<>();// 每层循环遍历，从左往右、从右往左的结果是否相等for(int i=0; i<levelCount; i++) {TreeNode node = queue.poll();// 节点值范围 -100 ~ 100，空节点可用极大或极小值填充if ( node == null ) {leftResult.offerLast(-1000);rightResult.offerFirst(-1000);}else {leftResult.offerLast(node.val);rightResult.offerFirst(node.val);queue.offer(node.left);queue.offer(node.right);}}// 每层从左往右、从右往左的结果是否相等，空节点用缺省值填充if (leftResult.equals(rightResult))continue;elsereturn false;}return true;}
}

LeetCode 1302. 层数最深叶子节点的和

• BFS，保留最后一层所有节点值的和。

class Solution {public int deepestLeavesSum(TreeNode root) {int sumResult = 0;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while( !queue.isEmpty() ) {int levelCount = queue.size();int levelSum = 0;for ( int i=0; i<levelCount; i++ ) {TreeNode node = queue.poll();levelSum += node.val;if ( node.left != null )queue.offer(node.left);if ( node.right != null )queue.offer(node.right);}sumResult = levelSum;}return sumResult;}
}