题目解析

首先我们来解析一下本题

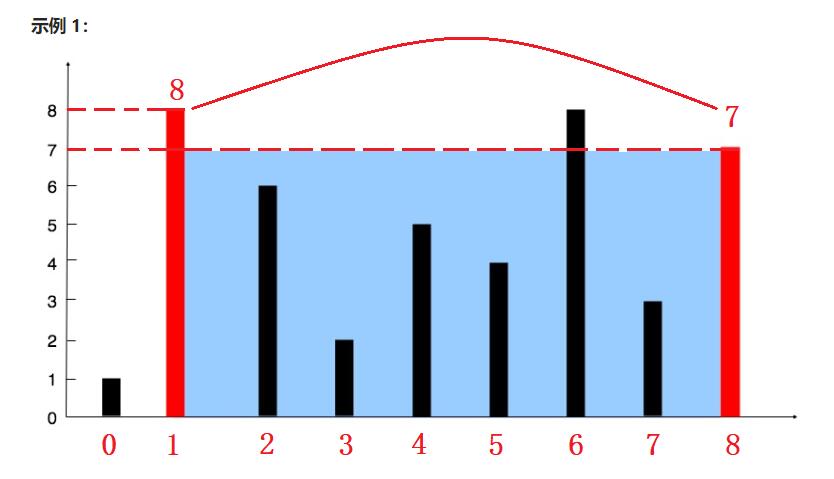
题目中说到，要找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

那我们现在来看最外侧的两根，一个高度为8，一个则为7，那我们肯定选择高度为7的，如果选择8的话就会出现溢出的问题；我们这里要求解的是可以容纳多少的水分，所以便要计算的是【容量】，那从第一根柱子到第八根的距离是多少呢？即8 - 1 = 7
所以最后的容量即为7 * 7 = 49

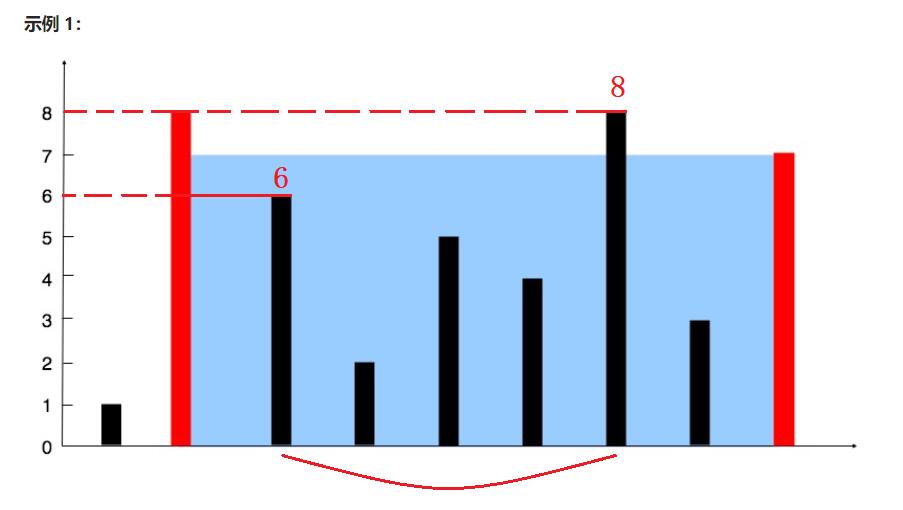
那我们再来看一个，高度取小的那个为6，宽度则取4，所以最后的容积为4 * 6 = 24，比49要来的小，但我们要取的是最大的那一个容量，所以还是取 49

💬 所以对于本题来说，我们初步的想法就是不断地去找两根柱子，然后计算出这两根柱子之间的所围成的容积大小，最后我们所要的则是最大的那一个容积

算法原理讲解

接下去呢我们再来讲解一下本题的算法原理

首先的话来讲解一下第一种方法，那就是我们同学最喜欢使用的【暴力枚举】，因为我们是不断地一一比较，所以直接使用双层for循环去进行实现即可。不过呢这种写法我试了一下是会超时的，所以立马放弃❌

接下去第二种，也是我要进行重点讲解的，那利用单调性，然后使用【双指针】来进行求解。因为我们在对两根柱子不断进行比较的时候，数字都会不停地发生变化，那么这里就会有两个情况：
- 第一种呢是比较的数字开始出现缩减的情况，即w变小；而且距离也开始缩减，即h变小，那w和h都进行缩减的话，最后的乘积[v]也会变得小
- 第二种的话则是所计算的数据不变，新的数据发生了放大，所以呢h不会缩小，不过距离的话还是会发生缩减，此时整体[v]也会变得小

那根据上面的分析，我们呢可以使用双指针去模拟遍历两个x轴的数据

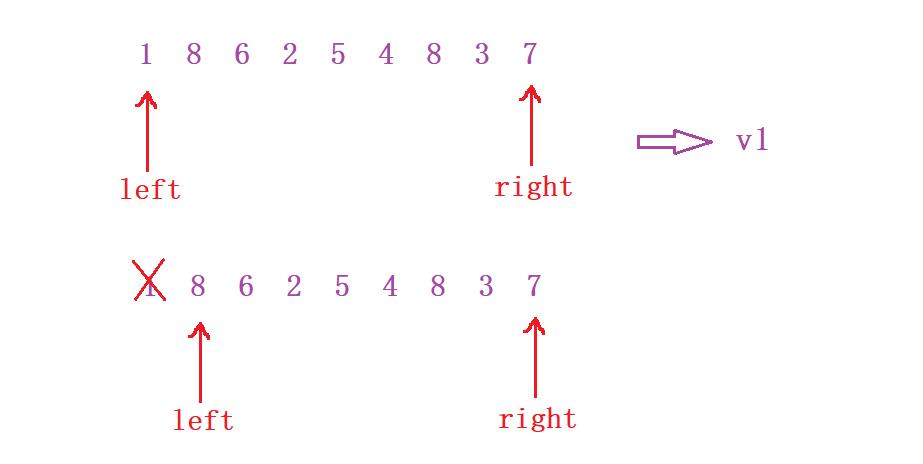
看到下面我们直接从两侧开始进行计算，那么在计算完得出第一个容量v1后，我们便可以直接舍弃这个【1】，因为其再与任何结合计算都会比【1】与【7】要来得小，原因在于距离会发生一个缩减

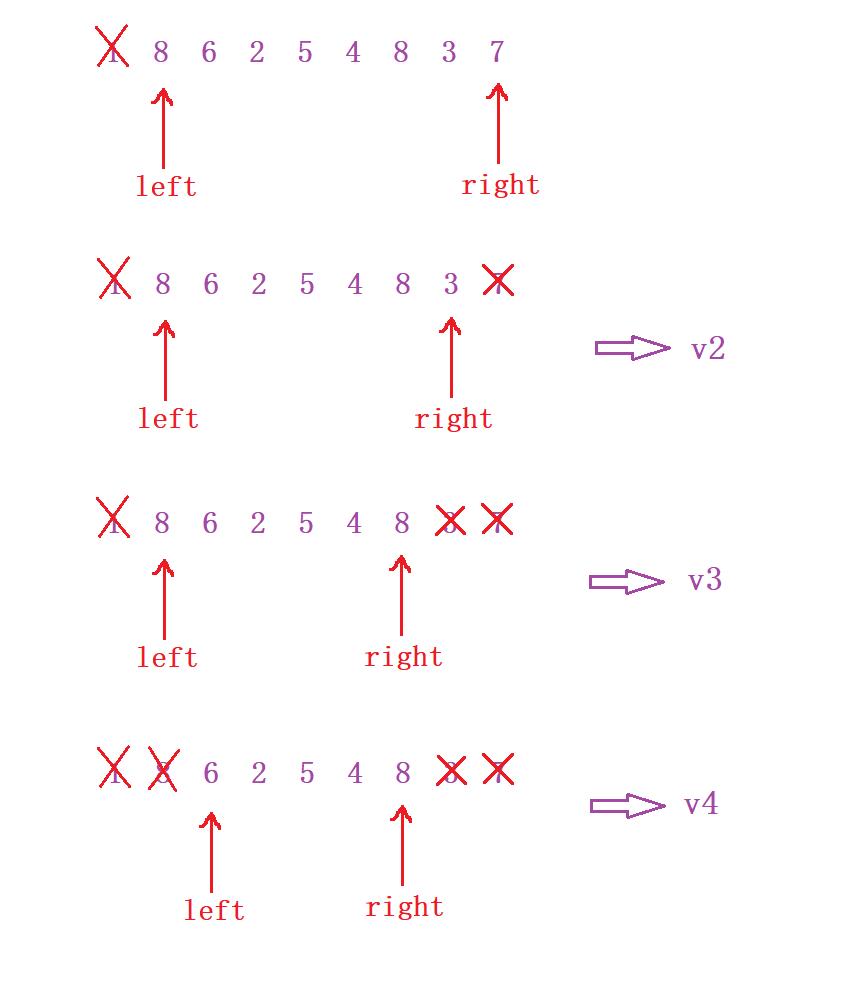
那接下去还是一样的思路，我们在使用双指针进行遍历的时候，只需要去判断二者的大小即可，左侧小的话就右移，右侧小的话就左移，然后记录下每一个容量v1、v2、v3，最后的话再去做一个比较即可

复杂度

时间复杂度:

对于时间复杂度而言，因为我们就是使用左右指针在遍历原先的数组，所以呢复杂度即为 $O (n)$

空间复杂度:

因为没开辟多余的空间，所以空间复杂度, 示例： $O (1)$

Code

以下是代码展示，读者可以根据我上面所分析的思路，自行去书写一下代码

可以看到，我在这里定义两个左右指针left和right，然后呢通过循环去遍历并计算它们两个位子上的数，计算的方法就是我们上面所讲，记住要去不断地更新最大值
当一轮计算完成之后不要忘记去更新left和right。最后当这个循环结束再去返回计算出来的最大值即可。

class Solution {
public:int maxArea(vector<int>& height) {int left = 0, right = height.size() - 1;int ret = 0;while(left < right){int v = min(height[left], height[right]) * (right - left);ret = max(v, ret);      // 更新最大值if(height[left] < height[right])    left++;else    right--;}return ret;}
};