暴力递归转动态规划（二）

上一篇已经简单的介绍了暴力递归如何转动态规划，如果在暴力递归的过程中发现子过程中有重复解的情况，则证明这个暴力递归可以转化成动态规划。
这篇帖子会继续暴力递归转化动态规划的练习，这道题有点难度。

题目
给定一个整型数组arr[]，代表数值不同的纸牌排成一条线。玩家A和玩家B依次拿走每张纸牌。规定玩家A先拿，玩家B后拿，但是每个玩家每次只能拿走最左边或者最右边的牌，玩家A和玩家B都绝顶聪明，请返回最后获胜者的分数。

暴力递归
依然是先从暴力递归开始写起，一个先手拿，一个后手拿，两个人都绝顶聪明，都知道怎么拿可以利益最大化。
先手的拿完第一个之后，再拿的时候，就要从后手拿完的数组里再挑选了。
同理，如果后手的等先手的拿了之后，是不是就可以从剩余的数组里挑选最大利益的拿了。
依然先确定base case：
如果先手拿，最理想的状态就是当数组剩下最后一个数，依然可以被我拿走。
如果后手拿，最悲催的连数组最后一个数我都拿不到。
代码中f()函数是代表在数组L~ R范围上返回上先手拿能拿到的最大值返回。
g()函数代表在数组L ~ R范围上后手拿，能够获取的最大值。
需要注意的是身份的转变，如果先手拿之后，再拿的时候就会变成后手，第二个后手拿的时候，虽然我是后手，但是也是从数组中挑选利益最大的拿，留给先手拿的人的也是不好的，所以我会变成先手。

//先手方法
public static int f(int[] arr,int L，int R){//base case:先手拿，并且数组中剩一个元素，我拿走if(L == R){return arr[L];}//因为可以选择从左边拿和右边拿，从左边拿下一次就是L + 1开始，右边拿就是 R - 1 开始。//需要注意的是我从左或者从右拿完之后，再拿就是拿别人拿剩下的了，要以后手姿态获取其余分数，所以要调用g()方法int p1 = arr[L] + g(arr,L + 1,R);int p2 = arr[R] + g(arr, L, R -1);//两种决策中取最大值return Math.max(p1,p2);
}
//后手方法
public static int g(int[] arr,int L,int R){//剩最后一个也不是我的，毛都拿不到，return 0if(L == R){return 0;}//后手方法是在先手方法后，挑选最大值，那如果先手方法选择了L，则我要从L + 1位置选，//如果先手选择了R，那我要从R - 1位置开始往下选。//是从对手选择后再次选择最大值int p1 = f(arr,L + 1,R);int p2 = f(arr,L,R - 1);//因为是后手，是在先手后做决定，是被迫的，所以取Min。return Math.min(p1,p2);
}

先手后手方法已经确定，来看主流程怎么调用

public static int win1(int[] arr){//如果是无效数组，则返回一个无效数字 -1 if(arr == null || arr.length == 0){return -1;}int first = f(arr, 0 ,arr.length - 1);int second = g(arr,0,arr.length - 1);return Math.max(first,second);
}

暴力递归的分析和代码已经搞定，接下来我们通过分析暴力递归的调用过程来实现第一步的优化，找它的依赖，找它的重复解。
举一个具体的例子，arr[]范围 0~ 7，根据上面暴力递归的代码逻辑，我们来看看它的依赖关系和调用过程。如果确定了可变参数以及依赖关系，是不是就可以尝试着优化成动态规划。
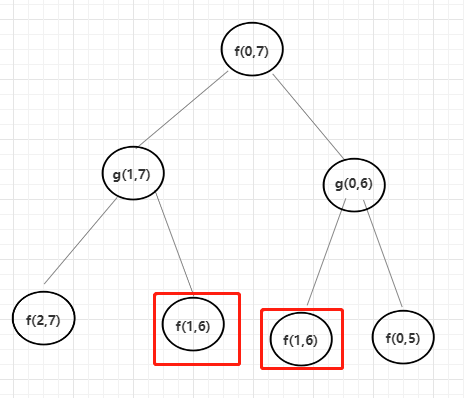
在这里插入图片描述
根据代码逻辑，要么是取左边L + 1，要么是取右边 R - 1，所以可以确定可变参数是L和R，并且整个流程下来会发现有重复解的情况。
不过有些不同的是，这个是双层递归循环依赖调用，所以如果根据可变参数参数L,R来构建缓存表的话，则需要2个不同的缓存表分别记录。

优化
前面已经分析出整个暴力递归的调用过程，并发现了重复解，其中可变参数是L、R，根据L、R构建缓存表，因为是f()和g()的循环依赖调用，所以需要准备两张缓存表。

public static int win2(int[] arr) {if (arr == null || arr.length == 0) {return -1;}int N = arr.length;int[][] fmap = new int[N][N];int[][] gmap = new int[N][N];for (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {fmap[i][j] = -1;gmap[i][j] = -1;}}int first = f1(arr, 0, arr.length - 1, fmap, gmap);int second = g1(arr, 0, arr.length - 1, fmap, gmap);return Math.max(first, second);}public static int f1(int[] arr, int L, int R, int[][] fmap, int[][] gmap) {// ！= -1，说明之前计算过该值，直接返回即可if (fmap[L][R] != -1) {return fmap[L][R];}int ans = 0;if (L == R){ans = arr[L];}else{int p1 = arr[L] + g1(arr, L + 1, R, fmap, gmap);int p2 = arr[R] + g1(arr, L, R - 1, fmap, gmap);ans = Math.max(p1, p2);}//这一步能够取得的最大值fmap[L][R] = ans;return ans;}public static int g1(int[] arr, int L, int R, int[][] fmap, int[][] gmap) {if (gmap[L][R] != -1){return gmap[L][R];}//因为如果 L == R，后手方法会返回0，默认ans也是等于0，省略一步判断int ans = 0;if (L != R){int p1 = f1(arr,L + 1,R,fmap,gmap);int p2 = f1(arr,L,R - 1,fmap,gmap);ans = Math.min(p1,p2);}gmap[L][R] = ans;return ans;}

二次优化
我们上面已经创建了缓存表，并找到了变量L、R，我们现在不妨举一个例子，并将缓存表画出来，来看一下表中每一列的对应关系，如果我们能找到这个缓存表的对应关系，是不是将表构建出来以后，就可以直接获取获胜者的最大值。
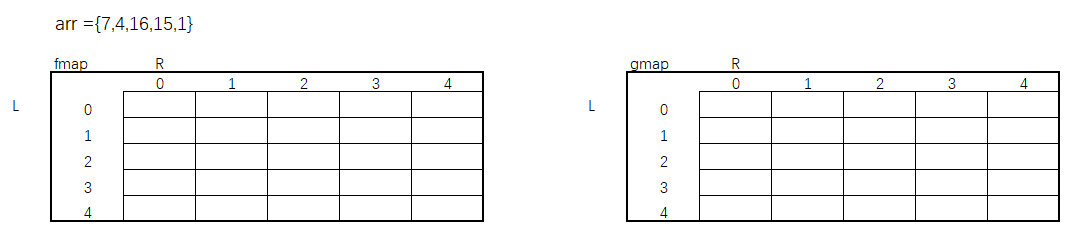
在这里插入图片描述
数组arr = {7,4,16,15,1} 因为有两张缓存表，所以需要将两张表的依赖关系都找出。接下来，回到最开始的暴力递归方法，根据代码逻辑一步一步找出依赖关系。

public static int win1(int[] arr) {if (arr == null || arr.length == 0) {return -1;}int first = f(arr, 0, arr.length - 1);int second = g(arr, 0, arr.length - 1);return Math.max(first, second);}public static int f(int[] arr, int L, int R) {if (L == R) {return arr[L];}int p1 = arr[L] + g(arr, L + 1, R);int p2 = arr[R] + g(arr, L, R - 1);return Math.max(p1, p2);}public static int g(int[] arr, int L, int R) {if (L == R) {return 0;}int p1 = f(arr, L + 1, R);int p2 = f(arr, L, R - 1);return Math.min(p1, p2);}

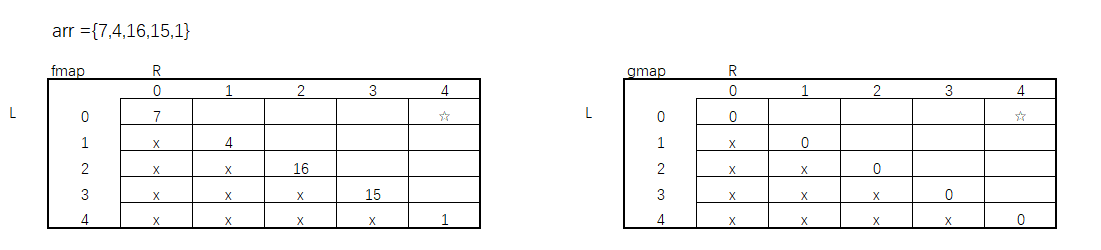
从先手方法f()和后手方法g()的base case可以看出，如果当L == R时，f()方法中此时就是等于数组arr[L]本身的值，而g()中为0，又因为，每次我只选L或只选R，当L = R时就return了，所以我的L始终不会 > R。我们所要求的L ~ R 范围是整个数组0 ~ 4的值，此时图可以填充成这样。
在这里插入图片描述
再来接着往下看，如果此时LR随便给一个值，比如说当前fmap中L = 1，R = 3，来接着看它的依赖过程。

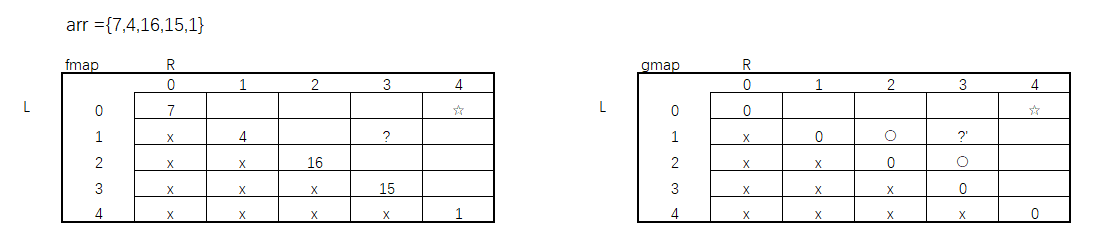
根据代码可以看出，它依赖的是g()方法中L +1和R - 1，所以对应在gmap中的依赖就是圆圈标记的部分。对应的，同样 L = 1 R = 3在gmap中也是依赖fmap对应的位置。
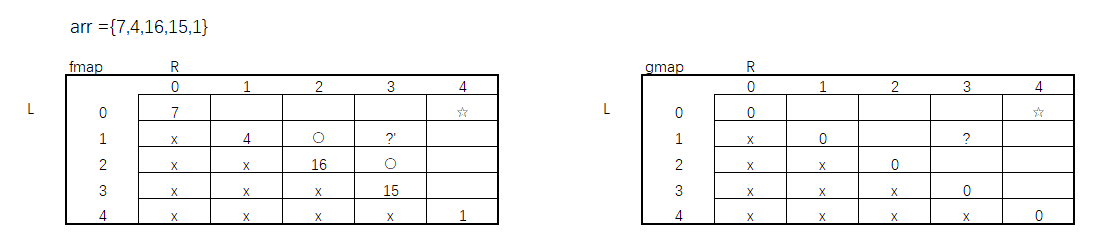
在这里插入图片描述
那现在有缓存表中每个位置的依赖关系，还有fmap和gmap当L == R时的值，是不是就可以推算出其他格子中的值。

代码

 public static int win3(int[] arr) {if (arr == null || arr.length == 0) {return -1;}int N = arr.length;int[][] fmap = new int[N][N];int[][] gmap = new int[N][N];//根据base  case填充fmap，gmap都是0，数组初始化值也是0，不用填充for (int i = 0; i < N; i++) {fmap[i][i] = arr[i];}//根据对角线填充，从第一列开始for (int startCol = 1; startCol < N; startCol++) {int L = 0;int R = startCol;while (R < N) {//将调用的g()和f()都替换成对应的缓存表fmap[L][R] = Math.max(arr[L] + gmap[L + 1][R], arr[R] + gmap[L][R - 1]);gmap[L][R] = Math.min(fmap[L + 1][R], fmap[L][R - 1]);L++;R++;}}//最后从L ~ R位置，取最大值return Math.max(fmap[0][N -1],gmap[0][N-1]);}