【1++的数据结构】之AVL树

👍作者主页：进击的1++
🤩 专栏链接：【1++的数据结构】

文章目录

  • 一，什么是AVL树
  • 二，AVL树的插入
  • 三，AVL树的旋转
    • 3.1 向左旋转
    • 3.2 向右旋转
    • 3.3 左右双旋
    • 3.4 右左双旋
  • 四，验证AVL树是否平衡

一，什么是AVL树

在说AVL树之前我们先来说说为什么会出现AVL树。在前面的文章中我们讲过二叉搜索树，虽然查找，插入效率比较高，但其有个缺陷：在某些情况下其可能会成为一颗单支树或其他高度较高的树，这时我们的效率就比较低了，甚至接近于O(n）。在此背景下，有两位俄罗斯数学家，便发明了AVL树----当插入新的结点后，保证每个结点的左右子树的高度差不大于1。则这颗树就会接近满二叉树，其高度就会降低，那么查找，插入效率也会提高。
在这里插入图片描述

二，AVL树的插入

在说AVL树的插入之前我们先来了解其结点。与二叉搜索树不同，其是三叉链结构和平衡因子，不但有左右指针，还有指向双亲结点的指针。这么设计的好处在于后面更新平衡因子是会比较方便。
我们来看结点结构代码：

template<class K, class V>struct AVLTreeNode{AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;pair<K, V> _kv;int _bf;//平衡因子AVLTreeNode(const std::pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0){}};

了解了结点的结构后，我们就可以进行插入操作的学习。
与二叉搜索树一样，其先要找到要插入的位置，代码如下;

if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;//给新结点找合适的位置while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}//与双亲结点进行链接cur = new Node(kv);if (parent->_kv.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;

与以前不同的是，由于是三叉链结构，因此当找到位置后，我们还要与其双亲结点进行链接。
当找到合适的位置进行插入后，便要进行控制平衡，使每个结点的左右子树高度差不超过1。

每个根节点的平衡因子的计算过程为;若插入的结点在其左侧，则根节点的平衡因子-1；若在右侧，则平衡因子+1。
根据平衡因子，我们总结出了三种控制平衡的规律:

  1. 若插入后根节点的平衡因子变为0，则说明在插入前其平衡因子为正负1，插入后被调整为0，满足AVL树的性质，则不做任何操作。
  2. 若插入后根节点的平衡因子变为正负1，则说明在插入前其平衡因子为0，插入后被改变，则向上继续更新，直到根节点。
  3. 若插入后平衡因子变为正负2，则违反了AVL树平衡的性质，需要进行旋转处理。

旋转操作，我们会在后面进行说明。

以下是控制其平衡的代码:

while (parent){if (cur == parent->_right){parent->_bf++;}else{parent->_bf--;}if (parent->_bf == 0){break;}else if (abs(parent->_bf) == 1){parent = parent->_parent;cur = cur->_parent;}else if (abs(parent->_bf) == 2){//左单旋if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}break;}else{assert(false);}}}

三，AVL树的旋转

3.1 向左旋转

以下是向左 旋转的代码：

void RotateL(Node* parent){Node* SubR = parent->_right;Node* SubRL = SubR ->_left;parent->_right = SubRL;if (SubRL){SubRL->_parent = parent;}Node* ppNode = parent->_parent;SubR->_left = parent;parent->_parent = SubR;if (_root == parent){_root = SubR;SubR->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = SubR;}else{ppNode->_right = SubR;}SubR->_parent = ppNode;}SubR->_bf = parent->_bf = 0;}

那么在什么情况下才会进行向左旋转呢？
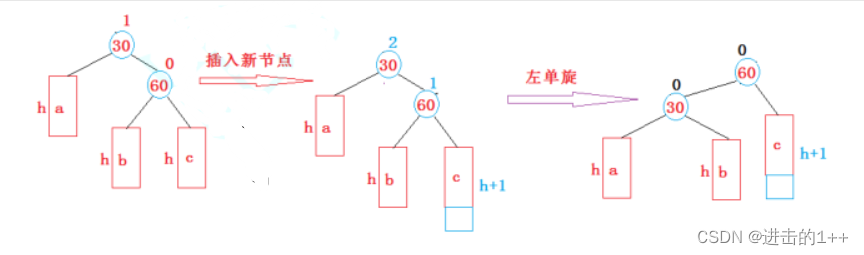
在这里插入图片描述

在这里插入图片描述

如图，当我们的新插入的结点在较高子数的右侧时，此时30这个结点的平衡因子变为了2，满足了旋转的条件（图中h可为任何正整数或0）我们可以从图中清楚的看到，当插入新节点后平衡因子为2的结点的右子数明显高，为了平衡，我们则需要给其右子树将高度，我们将30称为parent,60称为SubR;60的左子树b称为SubRL。从图中我们看到，SubR成为了这颗树或者说是子树的新结点。而SubRL成为了parent的右子树。改变后仍遵循二叉搜索树的规则。此时，我们的左旋转就完成了。旋转后，平衡因子也发生了改变，所以要对平衡因子进行更新。对parent和SubR的平衡因子进行更新，更新后都变为0。

3.2 向右旋转

向右旋转与向左旋转相似
代码如下：

void RotateR(Node* parent){Node* SubL = parent->_left;Node* SubLR = SubL->_right;parent->_left = SubLR;if (SubLR){SubLR->_parent = parent;}Node* ppNode = parent->_parent;SubL->_right = parent;parent->_parent = SubL;if (_root == parent){_root = SubL;SubL->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = SubL;}else{ppNode->_right = SubL;}SubL->_parent = ppNode;}SubL->_bf = parent->_bf = 0;}

向右旋转的情况如下图:
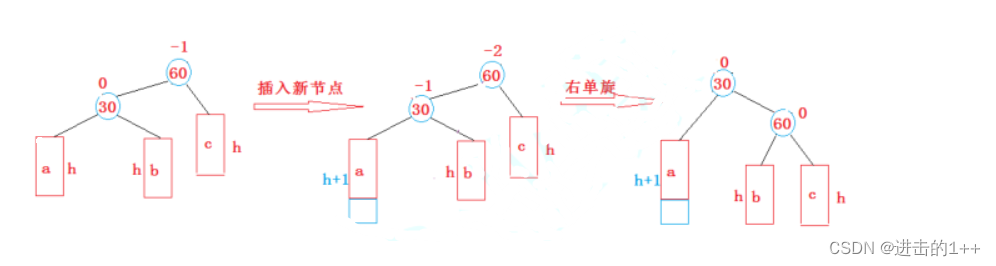
在这里插入图片描述
当新插入的结点在较高左子树的左侧时，进行右旋转。
如图，我们可以看出其左子树高，我们仍将60称为parent,将30称为SubL,将30的右子树称为SubLR。旋转时，将SubL作为了根节点，SubLR给了parent的左侧。旋转完成后要进行平衡因子的更新，parent与SubL都更新为0。

3.3 左右双旋

代码如下：

void RotateLR(Node* parent){Node* SubL = parent->_left;Node* SubLR = SubL->_right;int bf = SubLR->_bf;RotateL(parent->_left);RotateR(parent);SubLR->_bf = 0;if (bf == 1){parent->_bf = 0;SubL->_bf = -1;}else if (bf == -1){parent->_bf = 1;SubL->_bf = 0;}else if (bf == 0){parent->_bf = 0;SubL->_bf = 0;}else{assert(false);}}

当新结点插入较高左子树的右侧时，则会进行左右双旋，就是先向左旋转，再向右旋转。
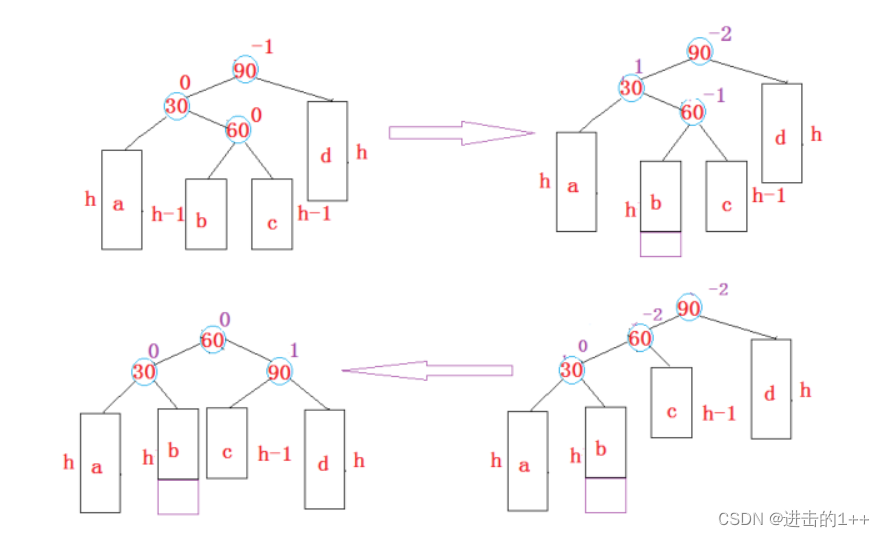
在这里插入图片描述
先以30为parent进行左旋转，再以90为parent进行右旋转。
左右旋转我们在上面已经进行了讲述，接下来，我们的重点是平衡 因此的更新，在上图这种情况下，新插入的结点可以为60的左子树，也可以为右子树，或者60本身就为新插入的结点。
因此在不能的情况下，平衡因子的更新也不同。
主要有以下情况：
（SubL为30，parent为90）

			Node* SubL= parent->_left;Node* SubLR = SubL->_right;int bf = SubLR->_bf;SubLR->_bf = 0;if (bf == 1){parent->_bf = 0;SubL->_bf = -1;}else if (bf == -1){parent->_bf = 1;SubL->_bf = 0;}else if (bf == 0){parent->_bf = 0;SubL->_bf = 0;}

3.4 右左双旋

代码如下:

void RotateRL(Node* parent){Node* SubR = parent->_right;Node* SubRL = SubR->_left;int bf = SubRL->_bf;RotateR(parent->_right);RotateL(parent);SubRL->_bf = 0;if (bf == 1){parent->_bf = -1;SubR->_bf = 0;}else if (bf == -1){parent->_bf = 0;SubR->_bf = 1;}else if (bf == 0){parent->_bf = 0;SubR->_bf = 0;}else{assert(false);}}

当新结点插入在较高右子树的左侧时，进行右左双旋（先向右旋转，在向左旋转）。
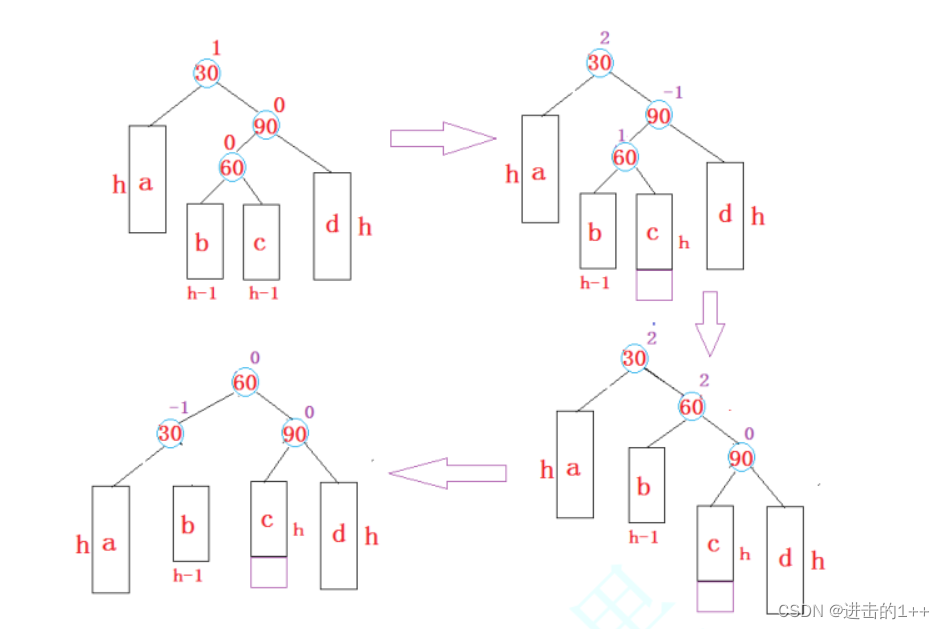
在这里插入图片描述
与左右双旋相似，其平衡因子的更新也有几种情况:

SubRL->_bf = 0;if (bf == 1){parent->_bf = -1;SubR->_bf = 0;}else if (bf == -1){parent->_bf = 0;SubR->_bf = 1;}else if (bf == 0){parent->_bf = 0;SubR->_bf = 0;}else{assert(false);}

四，验证AVL树是否平衡

AVL树最重要的一个性质就是其每个结点的左右子树之差的绝对值小于2。
并且等于该结点的平衡因子的绝对值。
我们以此来测试我们所写的AVL树是否正确
代码如下:


//求该子树的高度
int Height(Node* root){if (root == nullptr){return 0;}return max(Height(root->_left), Height(root->_right)) + 1;}bool _Isbalance(Node* root){if (root == nullptr){return true;}int leftHT = Height(root->_left);int rightHT = Height(root->_right);int diff = rightHT - leftHT;if (diff != root->_bf){cout << root->_kv.first << "平衡因子异常" << endl;return false;}return abs(diff) < 2 && _Isbalance(root->_left)&& _Isbalance(root->_right);}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/58430.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

LinkedList的顶级理解

LinkedList的顶级理解

目录 1.LinkedList的介绍 LinkedList的结构 2.LinkedList的模拟实现 2.1创建双链表 2.2头插法 2.3尾插法 2.4任意位置插入 2.5查找关键字 2.6链表长度 2.7遍历链表 2.8删除第一次出现关键字为key的节点 2.9删除所有值为key的节点 2.10清空链表 2.11完整代码 3.…
阅读更多...
①matlab的命令掌握

①matlab的命令掌握

目录 输入命令 命名变量 保存和加载变量 使用内置的函数和常量 输入命令 1.您可以通过在命令行窗口中 MATLAB 提示符 (>>) 后输入命令 任务 使用命令 3*5 将数值 3 和 5 相乘。 答案 3*5 2.除非另有指定&#xff0c;否则 MATLAB 会将计算结果存储在一个名为 ans…
阅读更多...
POI groupRow 折叠分组，折叠部分不显示问题

POI groupRow 折叠分组，折叠部分不显示问题

折叠组是什么&#xff1f;如图就是用POI 实现的&#xff0c;代码很简单&#xff1a;sheet.groupRow(开始行&#xff0c;结束行)即可 但是万万没想到&#xff0c;最终实现出的结果&#xff0c;合并的组&#xff0c;有一部分并没有渲染出来&#xff0c;如下图&#xff1a; 因为我…
阅读更多...
基于蜜獾算法优化的BP神经网络（预测应用） - 附代码

基于蜜獾算法优化的BP神经网络（预测应用） - 附代码

基于蜜獾算法优化的BP神经网络&#xff08;预测应用&#xff09; - 附代码 文章目录 基于蜜獾算法优化的BP神经网络&#xff08;预测应用&#xff09; - 附代码1.数据介绍2.蜜獾优化BP神经网络2.1 BP神经网络参数设置2.2 蜜獾算法应用 4.测试结果&#xff1a;5.Matlab代码 摘要…
阅读更多...
Android——基本控件（下）（十九）

Android——基本控件（下）（十九）

1. 菜单&#xff1a;Menu 1.1 知识点 &#xff08;1&#xff09;掌握Android中菜单的使用&#xff1b; &#xff08;2&#xff09;掌握选项菜单&#xff08;OptionsMenu&#xff09;的使用&#xff1b; &#xff08;3&#xff09;掌握上下文菜单&#xff08;ContextMenu&am…
阅读更多...
【会议征稿】2023智能通信与网络国际学术会议（ICN 2023）

【会议征稿】2023智能通信与网络国际学术会议（ICN 2023）

2023智能通信与网络国际学术会议&#xff08;ICN 2023&#xff09; 2023 International Conference on Intelligent Communication and Networking (ICN2023) 2023智能通信与网络国际学术会议&#xff08;ICN 2023&#xff09;将于2023年11月10-12日在中国常州召开。ICN 2023…
阅读更多...
Vue3+TS+Vite中 vConsole 插件的使用

Vue3+TS+Vite中 vConsole 插件的使用

平时在web应用开发过程中&#xff0c;我们可以console.log去输出一些信息&#xff0c;但是在移动端&#xff0c;也就是在手机上&#xff0c;console.log的信息我们是看不到的&#xff0c;这时候就需要移动端调试工具vConsole 1. 依赖安装 npm install vconsole 或者 yarn ad…
阅读更多...
扫雷小游戏

扫雷小游戏

目录 一.扫雷小游戏 二.游戏主体一览 ​编辑 三.模块化设计扫雷游戏 3.1打印欢迎菜单 3.2创建两个二维数组 3.3棋盘稍加修改 3.4布置雷 3.5排查雷 四.游戏总体代码 4.1game.h头文件 4.2game.c函数实现源文件 4.3游戏main函数主体 五.游戏效果图 一.扫雷小游戏 这是…
阅读更多...
Jmeter+ServerAgent

Jmeter+ServerAgent

一、Jmeter 下载 https://jmeter.apache.org/download_jmeter.cgi选择Binaries二进制下载 apache-jmeter-5.6.2.tgz 修改配置文件 jmeter下的bin目录&#xff0c;打开jmeter.properties 文件 languagezh_CN启动命令 cd apache-jmeter-5.6/bin sh jmeter二、ServerAgent 监…
阅读更多...
实战 图书馆系统管理案例

实战 图书馆系统管理案例

config &#xff1a;敏感的配置一般都是在配置中心配置&#xff0c;比如consul或者阿波罗上面controller &#xff1a;写一些handler的&#xff0c;拿到参数要去调用service层的逻辑。&#xff08;只负责接受参数&#xff0c;怎么绑定参数&#xff0c;要去调用哪个service的&am…
阅读更多...
Viobot输出数据说明

Viobot输出数据说明

一.原始数据 1.ROS话题 1)相机原始图像数据 Type: sensor_msgs::Image Topic: 左目&#xff1a;/image_left 右目&#xff1a;/image_right 2&#xff09;imu数据 Type: sensor_msgs::Imu Topic: /imu 3&#xff09;TOF数据 点云数据&#xff1a; Type: sensor_msgs::P…
阅读更多...
算法与数据结构（十）--图的入门

算法与数据结构（十）--图的入门

一.图的定义和分类 定义&#xff1a;图是由一组顶点和一组能够将两个顶点连接的边组成的。 特殊的图&#xff1a; 1.自环&#xff1a;即一条连接一个顶点和其自身的边; 2.平行边&#xff1a;连接同一对顶点的两条边&#xff1b; 图的分类&#xff1a; 按照连接两个顶点的边的…
阅读更多...
带你速览主数据管理（MDM）的前世今生

带你速览主数据管理（MDM）的前世今生

主数据管理的历史可以追溯到很久以前&#xff0c;可以说主数据管理是生产生活的一部分。随着社会生产力和生产工具的不断发展&#xff0c;主数据和主数据管理在其中的作用不断提升&#xff0c;成为当今政府、企业和社会团队等组织管理中必不可少基础管理工作&#xff0c;同时也…
阅读更多...
FrameBuffer 应用编程

FrameBuffer 应用编程

目录 什么是FrameBufferLCD 的基础知识使用ioctl()获取屏幕参数信息使用mmap()将显示缓冲区映射到用户空间 LCD 应用编程练习之LCD 基本操作LCD 应用编程练习之显示BMP 图片BMP 图像介绍在LCD 上显示BMP 图像在开发板上测试 在LCD 上显示jpeg 图像在LCD 上显示png 图片LCD 横屏…
阅读更多...
C语言_分支和循环语句（2）

C语言_分支和循环语句（2）

文章目录 前言一、for 循环1.1语法1.2 for 语句的循环控制变量1.3 一些 for 循环的变种 二、do ... while()循环2.1 do 语句的语法2.2 do ... while 循环中的 break 和 continue2.3 练习1 **- 计算n的阶乘**2. - **在一个有序数组中查找具体的某个数字 n** 二分查找算法&#x…
阅读更多...
68、使用aws官方的demo和配置aws服务，进行视频流上传播放

68、使用aws官方的demo和配置aws服务，进行视频流上传播放

基本思想：参考官方视频，进行了配置aws，测试了视频推流，rtsp和mp4格式的视频貌似有问题，待调研和解决 第一步：1) 进入aws的网站，然后进入ioT Core 2)先配置 Thing types & Thing，选择香港的节点，然后AWS ioT--->Manage---> Thing type 然后输入名字，创建Th…
阅读更多...
screen命令，可以断开服务器连接，依旧能运行你的程序了

screen命令，可以断开服务器连接，依旧能运行你的程序了

可以参考博客1&#xff1a;https://blog.csdn.net/nima_zhang_b/article/details/82797928 可以参考博客2:https://blog.csdn.net/herocheney/article/details/130984403 Linux中的screen是一个命令行工具&#xff0c;可以让用户在同一个终端会话中创建多个虚拟终端。它非常有…
阅读更多...
null值 字段运算

null值 字段运算

null值字段运算前先把null转成0 test表如下&#xff0c;num2为null select num1-num2 from test; 结果为null减去null值结果为null select sum(num1),SUM(num2) from test ;sum求和结果为null 判断字段是null不能用 null ,要用is null 错误写法&#xff1a; select IF(…
阅读更多...
Spring AOP基于注解方式实现和细节

Spring AOP基于注解方式实现和细节

目录 一、Spring AOP底层技术 二、初步实现AOP编程 三、获取切点详细信息 四、 切点表达式语法 五、重用&#xff08;提取&#xff09;切点表达式 一、Spring AOP底层技术 SpringAop的核心在于动态代理&#xff0c;那么在SpringAop的底层的技术是依靠了什么技术呢&#x…
阅读更多...
CSS按钮-跑马灯边框

CSS按钮-跑马灯边框

思路很简单&#xff0c;实现方法有很多很多。但是大体思路与实现方法都类似&#xff1a;渐变色 动画&#xff0c;主要区别在动画的具体实现 0、HTML 结构 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><titl…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023