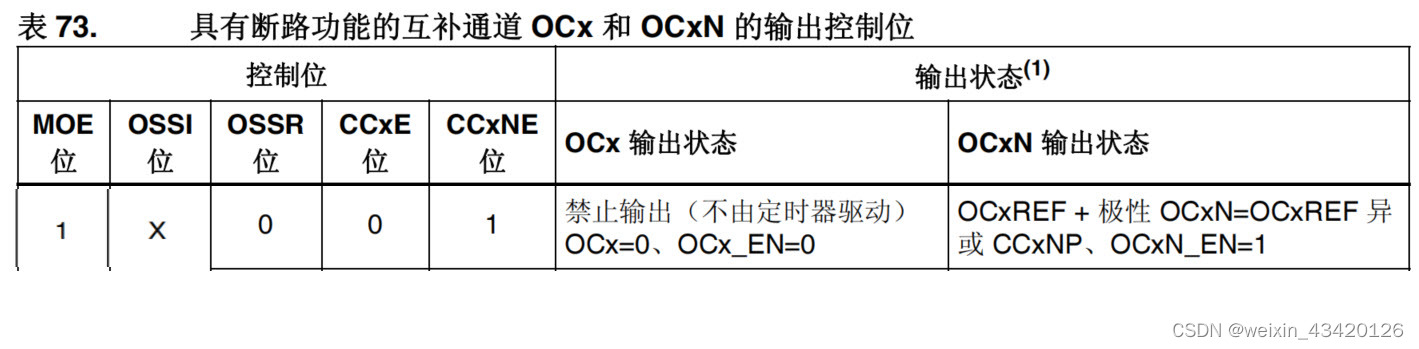
STM32F407-14.3.10-表73具有有断路功能的互补通道OCx和OCxN的输出控制位-1x001

如上表所示，MOE=1，OSSR=0，CCxE=0，CCxNE=1时，OCx输出状态取决于GPIO端口上下拉状态，OCxN输出状态取决于OCx_REF与极性选择（CCxNP）。

------------------------------------------------------------------------------------------------------------------------------

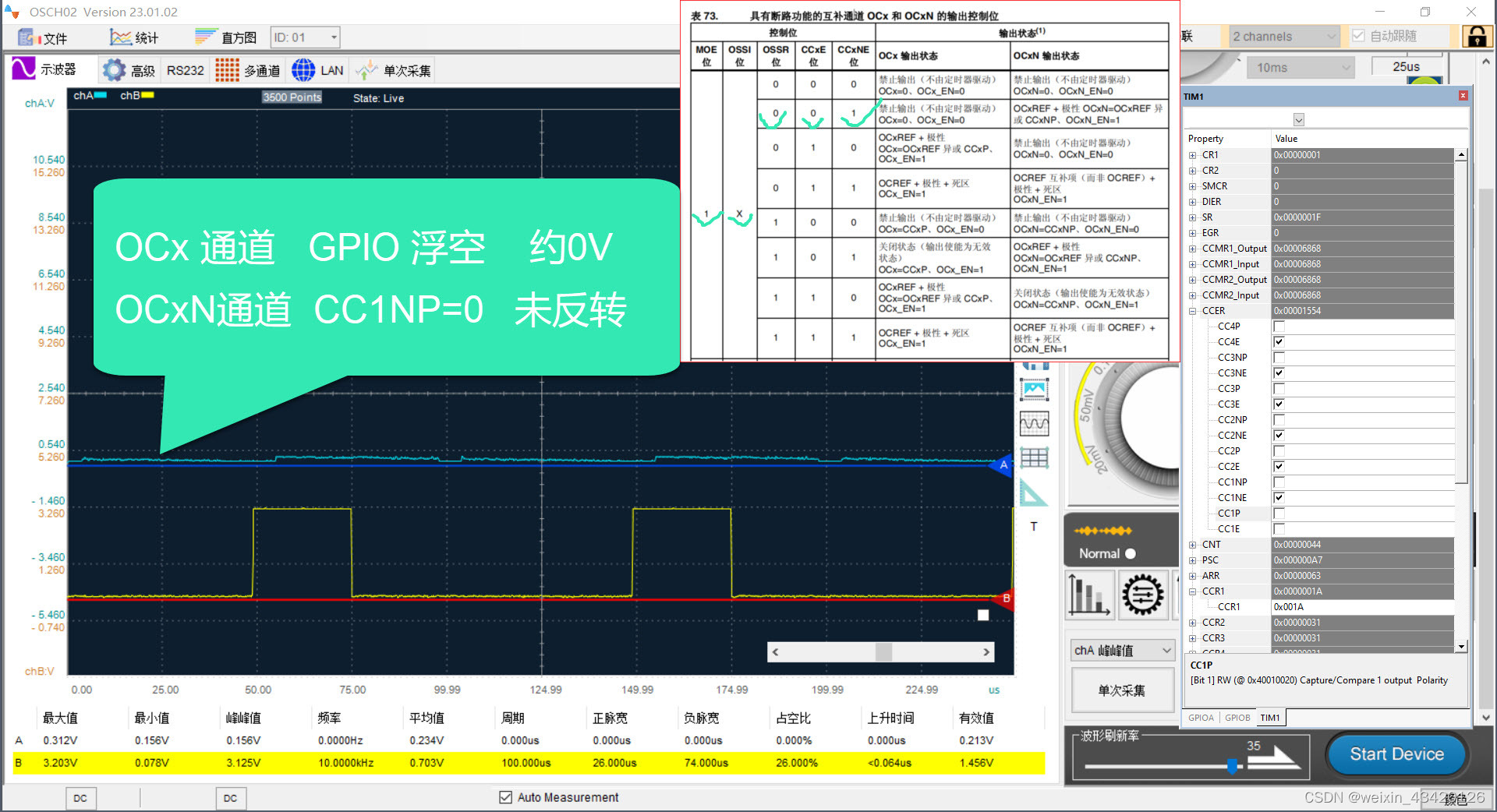
OCx复用的管脚初始化时配置为浮空，则OCx管脚电平位浮空（0V）

CCxNP=0， OCxN  通道极性  未反转  

------------------------------------------------------------------------------------------------------------------------------

OCx复用的管脚初始化时配置为浮空，则OCx管脚电平位浮空（0V）

CCxNP=1， OCxN  通道极性 反转  

------------------------------------------------------------------------------------------------------------------------------

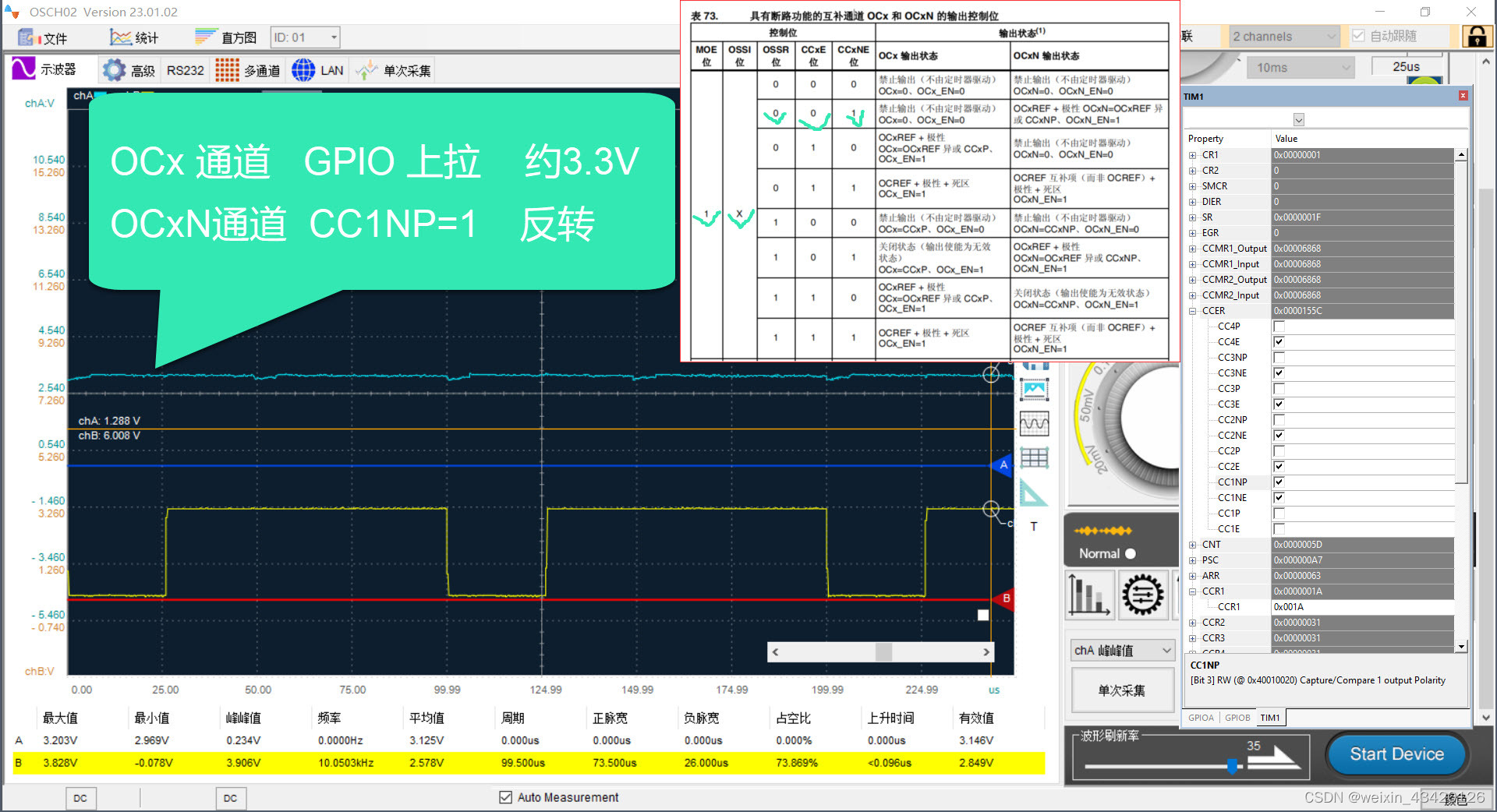
OCx复用的管脚初始化时配置为上拉，则OCx管脚上的电平为高电平（约3.3V）

CCxNP=0， OCxN  通道极性  未反转 

------------------------------------------------------------------------------------------------------------------------------

OCx复用的管脚初始化时配置为上拉，则OCx管脚上的电平为高电平（约3.3V）

CCxNP=1， OCxN  通道极性 反转  

------------------------------------------------------------------------------------------------------------------------------

OCx复用的管脚初始化时配置为下拉，则OCx管脚上的电平为低电平（约0V）

CCxNP=0， OCxN  通道极性  未反转 

------------------------------------------------------------------------------------------------------------------------------

OCx复用的管脚初始化时配置为下拉，则OCx管脚上的电平为低电平（约0V）

CCxNP=1， OCxN  通道极性 反转  

---------------------------------------------------------------------------------------------------------------------------------

补充CCxNP框图，方便理解波形

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/579895.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

【头歌实训】Spark 完全分布式的安装和部署（新）

【头歌实训】Spark 完全分布式的安装和部署（新）

文章目录 第1关： Standalone 分布式集群搭建任务描述相关知识课程视频Spark分布式安装模式主机映射免密登录准备Spark安装包配置环境变量修改 spark-env.sh 配置文件修改 slaves 文件分发安装包启动spark验证安装 编程要求测试说明答案代码 第1关： Stand…
阅读更多...
C++ Qt开发：QSqlDatabase数据库组件

C++ Qt开发：QSqlDatabase数据库组件

Qt 是一个跨平台C图形界面开发库，利用Qt可以快速开发跨平台窗体应用程序，在Qt中我们可以通过拖拽的方式将不同组件放到指定的位置，实现图形化开发极大的方便了开发效率，本章将重点介绍QSqlDatabase数据库模块的常用方法及灵活运用…
阅读更多...
Cloudstack多个管理服务器节点

Cloudstack多个管理服务器节点

https://docs.cloudstack.apache.org/en/4.18.0.0/adminguide/reliability.html 参考翻译： 代理上支持多个管理服务器 在具有多个管理服务器的Cloudstack环境中，可以根据算法配置代理，将其连接到哪个管理服务器。这对于内部负载均衡器或高可…
阅读更多...
【机器学习】人工智能概述

【机器学习】人工智能概述

人工智能（Artificial Intelligence，简称AI）是一门研究如何使机器能够像人一样思考、学习和执行任务的学科。它是计算机科学的一个重要分支，涉及机器学习、自然语言处理、计算机视觉等多个领域。 人工智能的概念最早可以追溯到20世…
阅读更多...
3.docker 安装失败

3.docker 安装失败

1、错误描述 2、报错前操作 ① 安装yum工具 yum install -y yum-utils \device-mapper-persistent-data \lvm2 --skip-broken ② 更新本地镜像源 # 设置docker镜像源 yum-config-manager \--add-repo \https://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo…
阅读更多...
扫描全能王启动鸿蒙原生应用开发，系HarmonyOS NEXT智能扫描领域首批

扫描全能王启动鸿蒙原生应用开发，系HarmonyOS NEXT智能扫描领域首批

近期，“鸿蒙合作签约暨扫描全能王鸿蒙原生应用开发启动仪式”（简称“签约仪式”）正式举行。合合信息与华为达成鸿蒙合作，旗下扫描全能王将基于HarmonyOS NEXT正式启动鸿蒙原生应用开发。据悉，扫描全能王是鸿蒙在智能扫…
阅读更多...
DM、HIVE和Kingbase8(人大金仓数据库)给列增加备注

DM、HIVE和Kingbase8(人大金仓数据库)给列增加备注

DM数据库给列增加备注 1、创建表 CREATE TABLE test222 ( id int NOT NULL PRIMARY KEY, name varchar(1000) DEFAULT NULL, email varchar(1000) DEFAULT NULL, phone varchar(1000) DEFAULT NULL ) 2、给列添加注释 comment on column TEST222.NAME is 这是一个列注释; 例如…
阅读更多...
说说 Spring Boot 实现接口幂等性有哪几种方案？

说说 Spring Boot 实现接口幂等性有哪几种方案？

一、什么是幂等性 幂等是一个数学与计算机学概念，在数学中某一元运算为幂等时，其作用在任一元素两次后会和其作用一次的结果相同。 在计算机中编程中，一个幂等操作的特点是其任意多次执行所产生的影响均与一次执行的影响相同。幂等函数或幂等…
阅读更多...
关联规则+聚类分析+分类算法(数据挖掘)

关联规则+聚类分析+分类算法(数据挖掘)

3.关联规则 经典案例 : 尿布与啤酒的故事； 基本概念 : 设I {i1,i2,....im}是项(Item)的集合。 D 是 事务(transaction)的集合(事务数据库)。 事务T是项的集合，且对每个事务具有唯一的标识: 事务号，记作TID; 设A是I中的一个项集&#xf…
阅读更多...
Redis分布式缓存之主从哨兵分片集群

Redis分布式缓存之主从哨兵分片集群

Redis主从 数据同步原理 Redis哨兵 Redis分片集群 集群伸缩：在集群中插入或删除某个节点 集群故障转移
阅读更多...
Android 13 - Media框架（28）- ACodec（五）

Android 13 - Media框架（28）- ACodec（五）

前面几节我们了解了OMXNodeInstance是如何处理setPortMode、allocateBuffer、useBuffer的，这一节我们再回到ACodec，来看看 ACodec start 的其他部分。 我们首先来回顾一下，ACodec start 的状态切换以及处理的事务，我们用一张不太准…
阅读更多...
「GPT」G、P、T分别是啥意思？

「GPT」G、P、T分别是啥意思？

G意为Generative ：生成式 比如，生成式的分类器（模型）包括---- generative classifiers: naive Bayes classifier and linear discriminant analysis 与之对应的为判别式----- discriminative model: logistic regression P意为…
阅读更多...
基于 Linux 的批量上传本地 Git 仓库到 Github 的实践

基于 Linux 的批量上传本地 Git 仓库到 Github 的实践

基于 Linux 的批量上传本地 Git 仓库到 Github 的实践 一、需求二、上传本地 Git 仓库2.1 初始版本2.2 优化版本 三、 GitHub 创建空仓库3.1 初始版本3.2 优化版本 一、需求 app目录下的每个文件夹都是一个git仓库，如何使用shell脚本将所有git仓库都上传到github上…
阅读更多...
记一次Mac端mysql重置密码

记一次Mac端mysql重置密码

在执行mysql命令的时候，报如下的错误，表示不支持mysql命令： zsh: command not found: mysql 1. 先查看mysql服务是否存在 在系统偏好设置中查看： 2. 发现mysql服务已经在运行，可能因为/usr/local/bin目录下缺失mysq…
阅读更多...
如何使用设计模式来解决类与类之间调用过深的问题。

如何使用设计模式来解决类与类之间调用过深的问题。

我们将使用责任链模式和装饰者模式的组合。 考虑一个简化的餐厅订单处理系统，其中包括服务员（Waiter）、厨师（Chef）和收银员（Cashier）。订单从服务员开始，然后传递给厨师&#xff0c…
阅读更多...
ubuntu22.04搭建RTSP服务器

ubuntu22.04搭建RTSP服务器

大致命令如下： git clone --depth 1 gitgithub.com:ZLMediaKit/ZLMediaKit.git sudo apt-get install build-essential sudo apt-get install cmake #除了openssl,其他其实都可以不安装 sudo apt-get install libssl-dev sudo apt-get install libsdl-dev sudo apt…
阅读更多...
linux基于用户身份对资源访问进行控制的解析及过程

linux基于用户身份对资源访问进行控制的解析及过程

linux中用户分为三类 1.超级用户（root） 拥有至高无上的权限 2.普通用户 人为创建、权限小，权限受到控制 3.程序用户 运行程序的用户，不是给人使用的，给程序使用的，一般不给登录！ 组账…
阅读更多...
【LeetCode刷题笔记（13-1）】【Python】【回文数】【反转整数】【简单】

【LeetCode刷题笔记（13-1）】【Python】【回文数】【反转整数】【简单】

文章目录 引言回文数题目描述提示 题意分析解决方案1：【反转字符串】解决方案2：【反转整数】题外话结束语 9. 回文数 引言 编写通过所有测试案例的代码并不简单，通常需要深思熟虑和理性分析。虽然这些代码能够通过所有的测试案例&#xff0…
阅读更多...
【AI】人工智能爆发推进器之卷积神经网络

【AI】人工智能爆发推进器之卷积神经网络

目录 一、什么是卷积神经网络 1. 卷积层（Convolutional Layer） 2. 激活函数（Activation Function） 3. 池化层（Pooling Layer） 4. 全连接层（Fully Connected Layer） 5. 训练过程…
阅读更多...
html table+css实现可编辑表格

html table+css实现可编辑表格

要实现可编辑的 HTML 表格&#xff0c;你可以使用 JavaScript 和 HTML5 的 contenteditable 属性。 <!DOCTYPE html> <html> <head><style>table {border-collapse: collapse;width: 100%;}th, td {border: 1px solid black;padding: 8px;text-align:…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023