Every day a Leetcode

题目来源：2928. 给小朋友们分糖果 I

解法1：暴力

枚举 3 位小朋友的糖果数，范围为 [0, limit]，分别记为 i、j、k。

当满足 i + j + k == n 时，答案 +1。

代码：

/** @lc app=leetcode.cn id=2928 lang=cpp** [2928] 给小朋友们分糖果 I*/// @lc code=start// 暴力class Solution
{
public:int distributeCandies(int n, int limit){int count = 0;for (int i = 0; i <= limit; i++)for (int j = 0; j <= limit; j++)for (int k = 0; k <= limit; k++)if (i + j + k == n)count++;return count;}
};
// @lc code=end

结果：

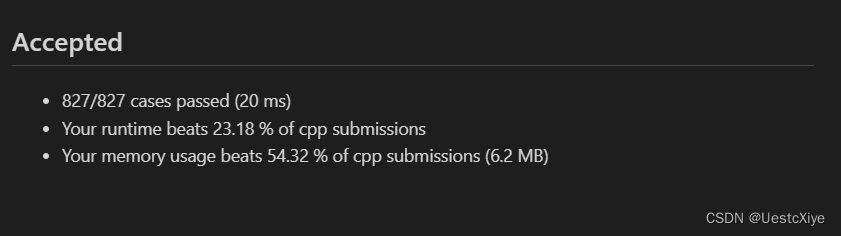
复杂度分析：

时间复杂度：O(limit³)，其中 limit 是 1 名小朋友能得到的糖果数的最大值。

空间复杂度：O(1)。

解法2：一次遍历

将第 1 个小朋友得到的糖果数记为 i，第 2 个小朋友和第 3 个小朋友得到的糖果总数为 remain=n−i。由于每个小朋友得到的糖果数都不超过 limit，因此应满足如下条件：

1. 第 1 个小朋友得到的糖果数的范围是 [0,limit]，即 i≤limit。

2. 第 2 个小朋友和第 3 个小朋友得到的糖果总数的范围是 [0,limit×2]，即 0≤remain≤limit×2。

将 remain=n−i 代入，整理得到 max⁡(0,n−limit×2)≤i≤min⁡(n,limit)。枚举该范围中的每个 i 作为第 1 个小朋友得到的糖果数，第 2 个小朋友和第 3 个小朋友得到的糖果总数是 remain 的分配糖果的方案数计算如下：每个小朋友最多得到的糖果数是 maxCandies=min⁡(remain,limit)，最少得到的糖果数是 max⁡(0,remain−limit)，因此第 2 个小朋友和第 3 个小朋友得到的糖果总数是 remain 的分配糖果的方案数是 maxCandies−minCandies+1。

遍历所有的 i 之后，即可得到分配糖果的方案数。

代码：

// 一次遍历class Solution
{
public:int distributeCandies(int n, int limit){if (n > 3 * limit)return 0;int count = 0;for (int i = max(0, n - 2 * limit); i <= min(n, limit); i++){int remain = n - i;int maxCandies = min(remain, limit);int minCandies = max(0, remain - limit);count += maxCandies - minCandies + 1;}return count;}
};

结果：

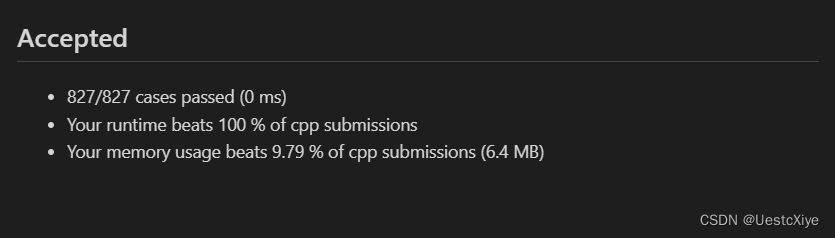
复杂度分析：

时间复杂度：O(min(n, limit))，其中 n 是分配的糖果总数，limit 是每个小朋友得到的糖果数的上限。

空间复杂度：O(1)。

解法3：容斥原理

题解：【灵茶山艾府】O(1) 容斥原理（Python/Java/C++/Go）

代码：

// 容斥原理class Solution
{int c2(int n){return n > 1 ? n * (n - 1) / 2 : 0;}public:int distributeCandies(int n, int limit){return c2(n + 2) - 3 * c2(n - limit + 1) + 3 * c2(n - 2 * limit) - c2(n - 3 * limit - 1);}
};

结果：

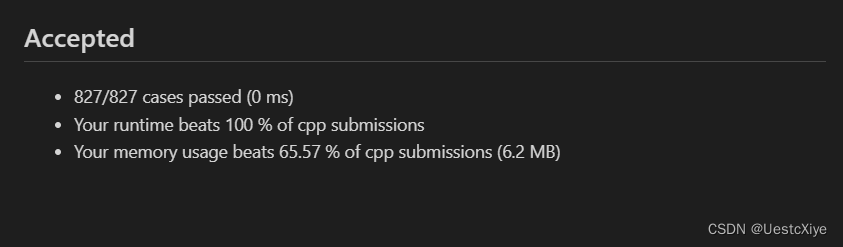
复杂度分析：

时间复杂度：O(1)。

空间复杂度：O(1)。