Python - 深夜数据结构与算法之 Divide Conquer Backtrack

一.引言

二.分治与回溯简介

1.Divide & Conquer 分治

2.BackTrack 回溯

三.经典算法实战

1.Combination-Of-Phone [17]

2.Permutations [46]

3.Permutations-2 [47]

4.Pow-X [50]

5.N-Queen [51]

6.Combinations [78]

7.Sub-Sets [78]

8.Majority-Element [169]

四.总结

一.引言

分治与回溯本质上也是递归的一种，其相对传统递归稍微复杂一些，涉及到最后一步状态的恢复，下面我们学习下二者的特性与题目。

二.分治与回溯简介

1.Divide & Conquer 分治

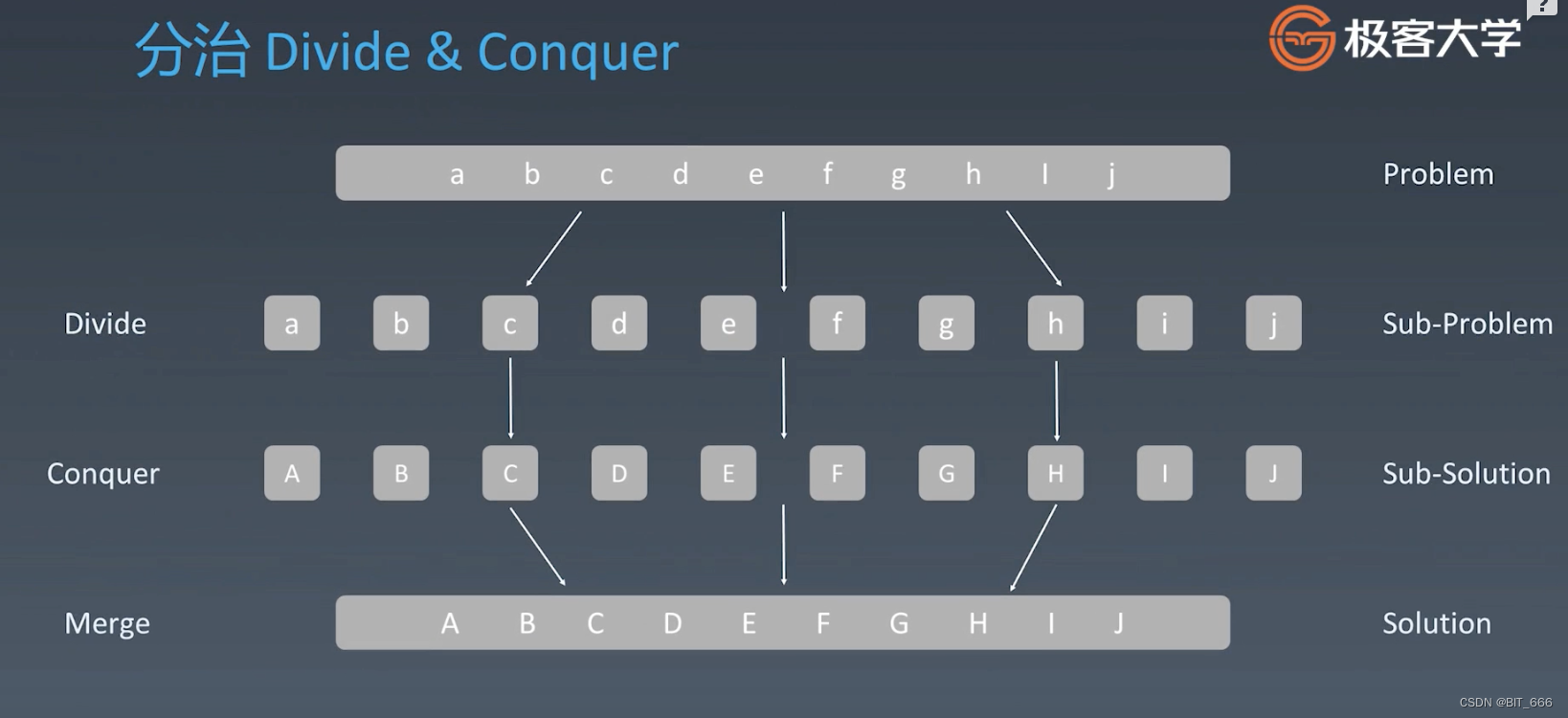
分治的思路整体和递归是一样的，我们需要先将 Problem 转化为子问题 Sub-Problem，然后针对每个 Sub-Problem 进行解决，最后将多个 Sub-Solution 合并得到最终结果，下面的代码模版就是按照上面的思路来实现。

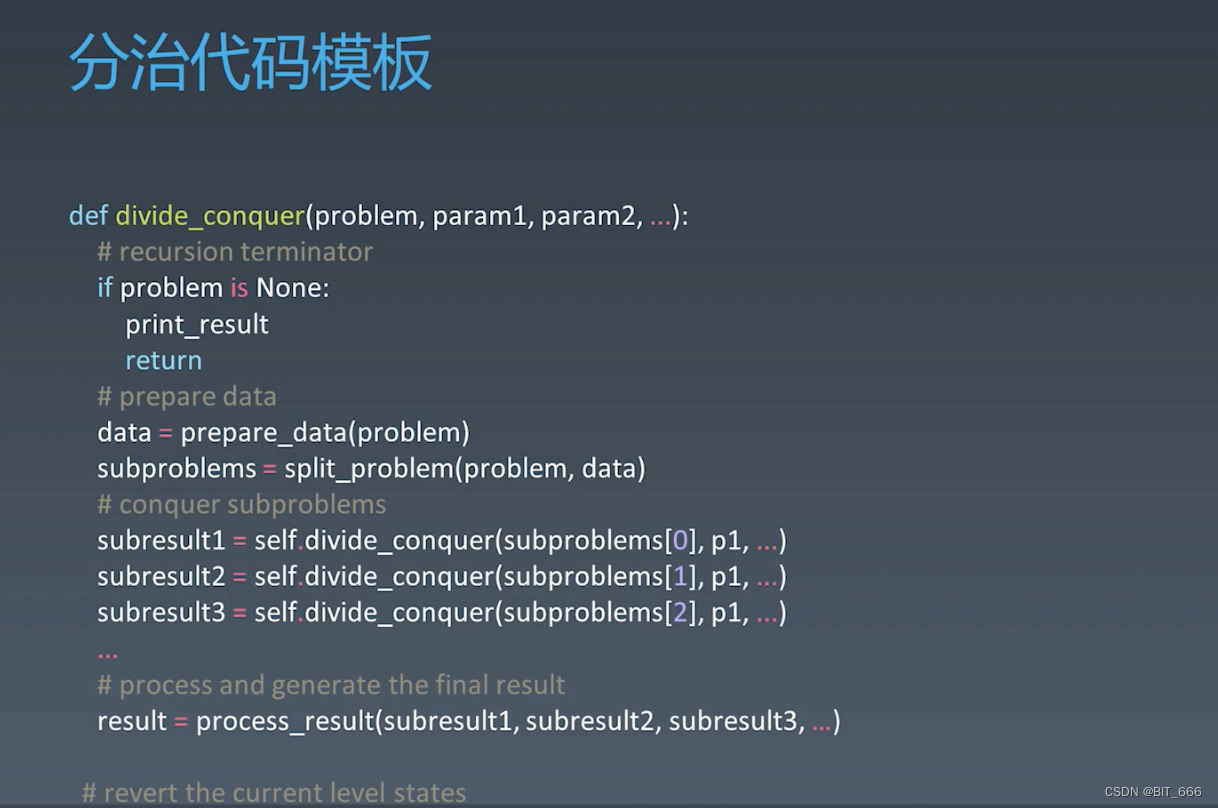
2.BackTrack 回溯

基于 base 情况，不断向前试探，试探成功找到结果，试探失败回撤，并且恢复上一步的状态。

三.经典算法实战

1.Combination-Of-Phone [17]

电话号码组合: https://leetcode.cn/problems/letter-combinations-of-a-phone-number/description/

◆ 题目分析

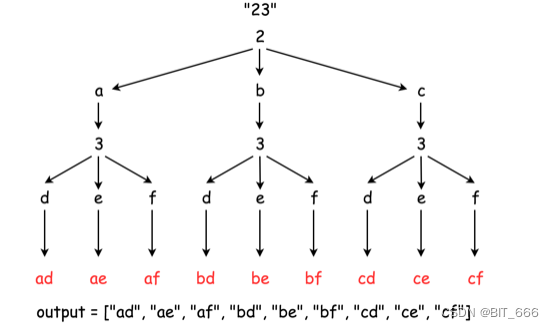
分别获取数字及其对应的字符，逐层遍历即可。

◆ 回溯实现

class Solution(object):def letterCombinations(self, digits):""":type digits: str:rtype: List[str]"""if not digits:return []phone_map = {"2": "abc","3": "def","4": "ghi","5": "jkl","6": "mno","7": "pqrs","8": "tuv","9": "wxyz"}combination = []res = []def backtrack(position):if position == len(digits):res.append("".join(combination))return # 遍历当前数字的多个字母digit = digits[position]for letter in phone_map[digit]:combination.append(letter)backtrack(position + 1)combination.pop()backtrack(0)return res

人肉递归的方式可以参考这个图理解。

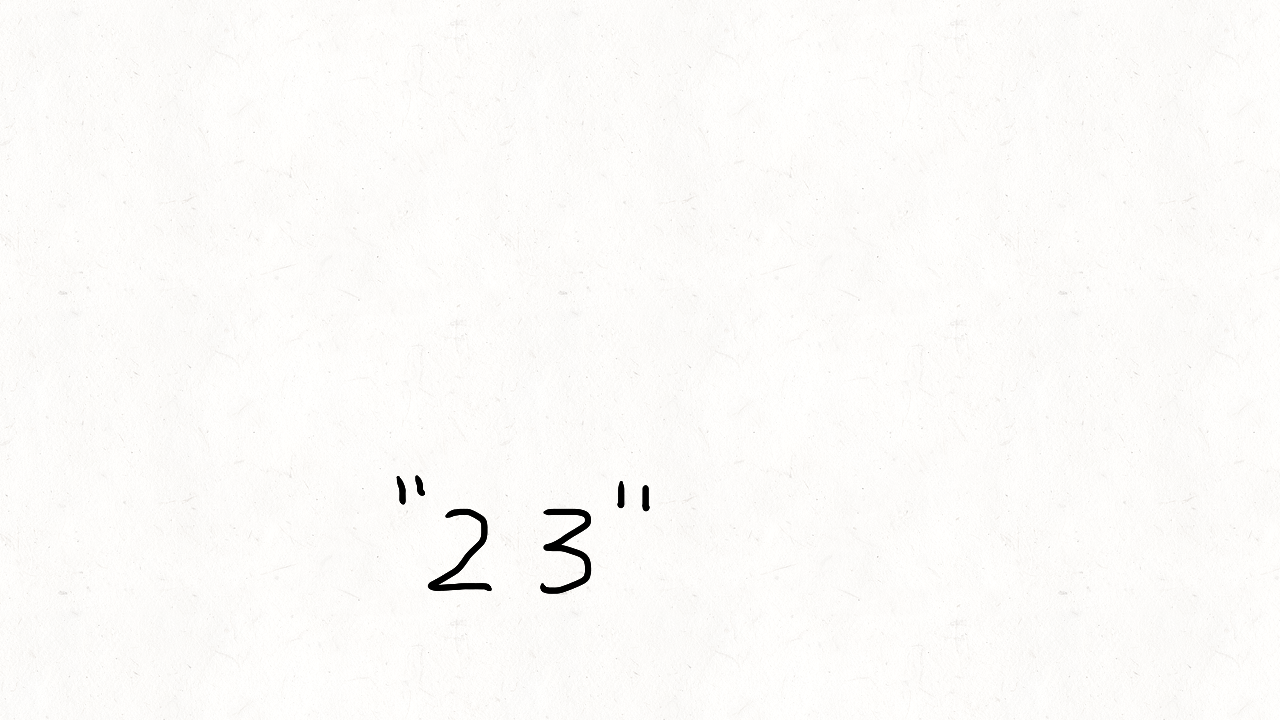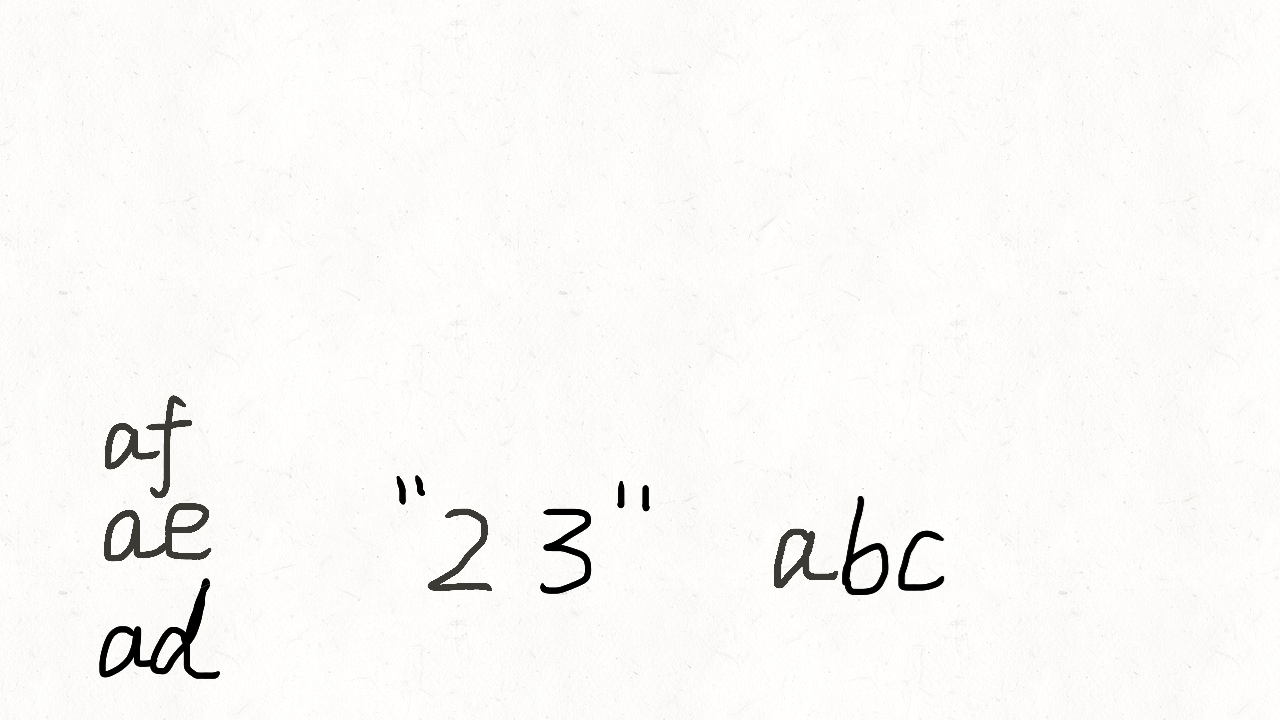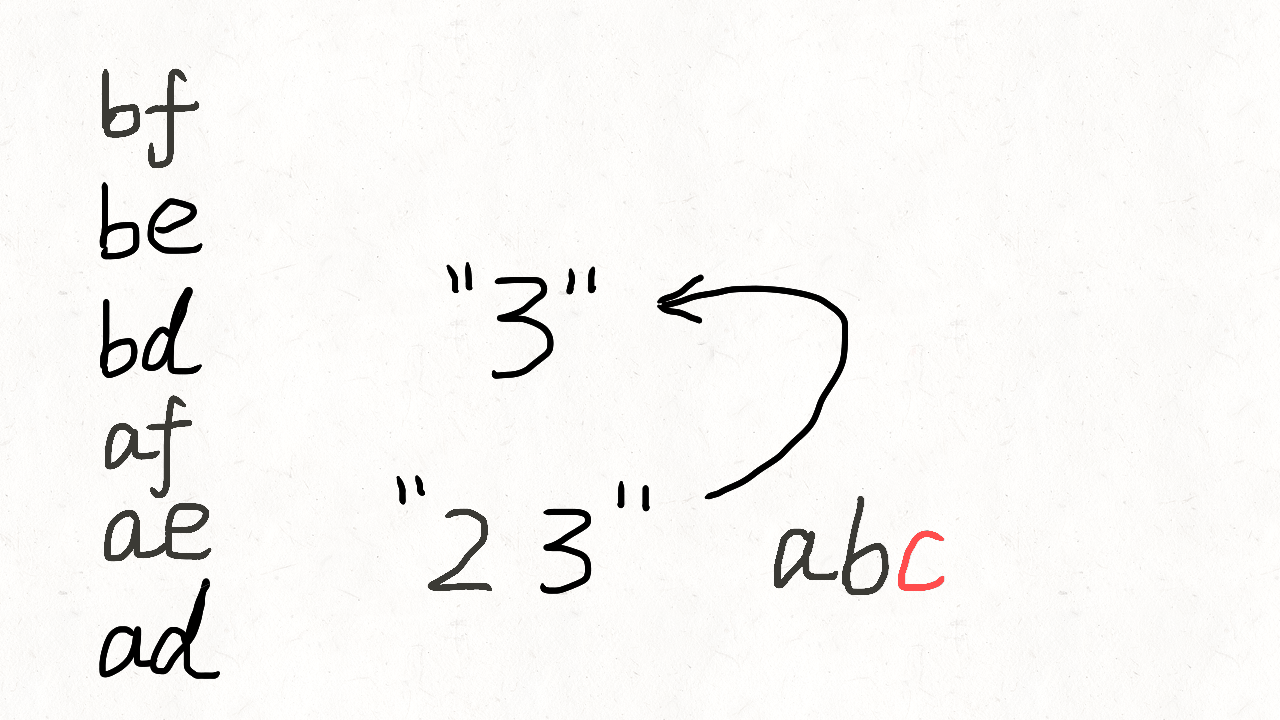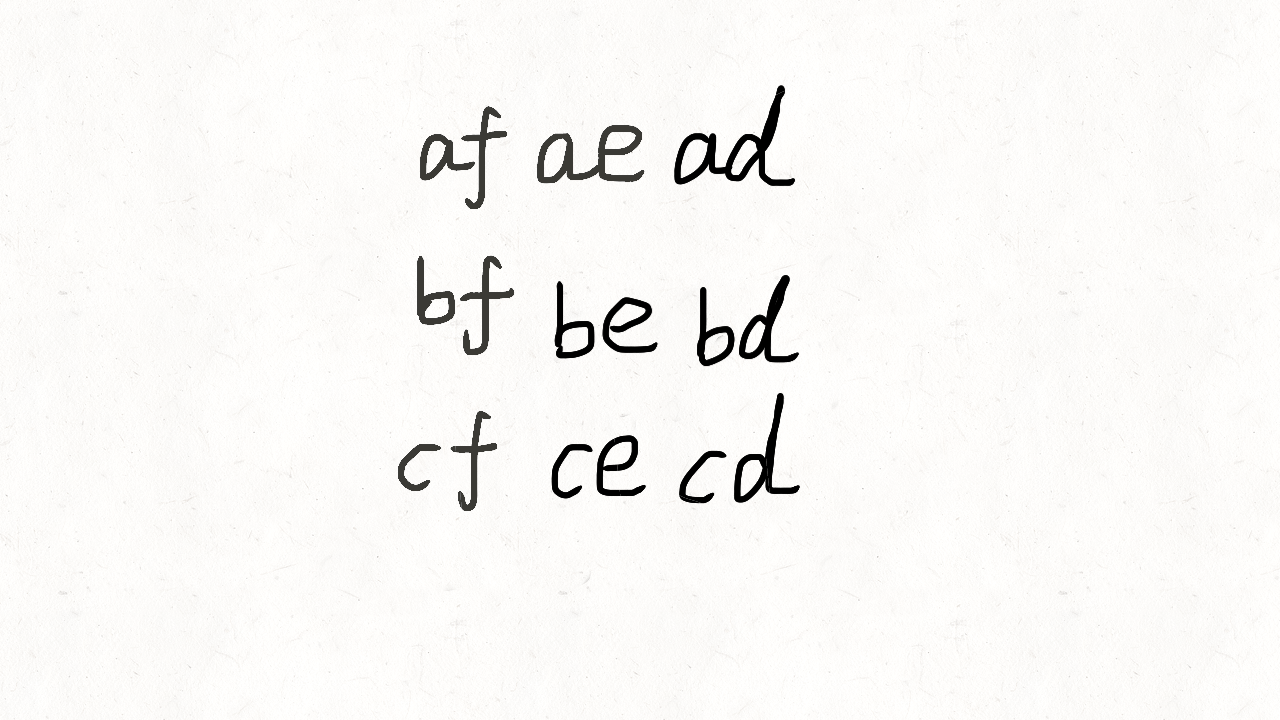
2.Permutations [46]

全排列: https://leetcode-cn.com/problems/permutations/

◆ 题目分析

按照回溯思路实现，从 0 到 len(nums) 固定每个位置，将该元素与其后方元素依次调换位置，直至最后一个元素即可。

◆ 回溯实现

class Solution(object):def permute(self, nums):""":type nums: List[int]:rtype: List[List[int]]"""res = []def backtrack(position, end):if position == end:res.append(nums[:])returnfor i in range(position, end):nums[i], nums[position] = nums[position], nums[i]backtrack(position + 1, end)nums[i], nums[position] = nums[position], nums[i]backtrack(0, len(nums))return res

第一次循环遍历位置 0，因为 replace 的原因，所以位置 0 上每个元素都会出现一次，在该基础上，固定第一个位置，分别将剩余元素分别替换至位置 1，以此类推。可以理解为第一次循环把位置 0 的所有可能遍历一遍， [0] [1] [2] 这样，第二次基于前面的基础 [0, 1] [0,2]、[1,0] [1, 2] 这样，... 以此类推。

3.Permutations-2 [47]

全排列2: https://leetcode.cn/problems/permutations-ii/

◆ 题目分析

按照回溯思路实现，从 0 到 len(nums) 固定每个位置，将该元素与其后方元素依次调换位置，直至最后一个元素即可。和上面方法一致。

◆ 回溯实现

class Solution(object):def permuteUnique(self, nums):""":type nums: List[int]:rtype: List[List[int]]"""res = []# 回溯起始位置def backtrack(position, end):if position == end:res.append(nums[:])returnfor i in range(position, end):# position 位置的 N 种可能nums[position],nums[i] = nums[i], nums[position]# 固定 position 位置，在此基础上固定 position + 1 的位置backtrack(position + 1, end)# 回复原始状态供后面 position 从初始状态遍历nums[position],nums[i] = nums[i], nums[position]backtrack(0, len(nums))res = list(set(tuple(sub) for sub in res))res = [list(sub) for sub in res]return res

在上一题的基础上进行去重，set 支持 tuple 不支持 list 去重，所以需要转换，时空复杂度都比较高。

◆ 去重优化

class Solution(object):def permuteUnique(self, nums):""":type nums: List[int]:rtype: List[List[int]]"""res = []# 回溯起始位置def backtrack(position, end):if position == end:res.append(nums[:])returnrepeat = set()for i in range(position, end):if nums[i] in repeat:continuerepeat.add(nums[i])# position 位置的 N 种可能nums[position],nums[i] = nums[i], nums[position]# 固定 position 位置，在此基础上固定 position + 1 的位置backtrack(position + 1, end)# 回复原始状态供后面 position 从初始状态遍历nums[position],nums[i] = nums[i], nums[position]backtrack(0, len(nums))return res

最后全局去重的时间、空间复杂度都很高，我们修改为递归内判断，在 for 循环之前增加 set，如果 position-end 区间有相同元素则直接 continue 跳过即可。

4.Pow-X [50]

求 x 的 n 次方: https://leetcode.cn/problems/powx-n/description/

◆ 题目分析

Problem = 2^10，sub-problem = 2^5，我们处理的话就是 2^ (n/2)

Problem = 2^5，sub-problem = 2^2，我们处理的话还是 2^ (n/2)，但是遗漏一个 2

所以我们还需要区分 n/2 是否整除，整除 x^n = x^(n/2) * x^(n/2) 不整除则再多乘一个 2。

◆ 递归实现

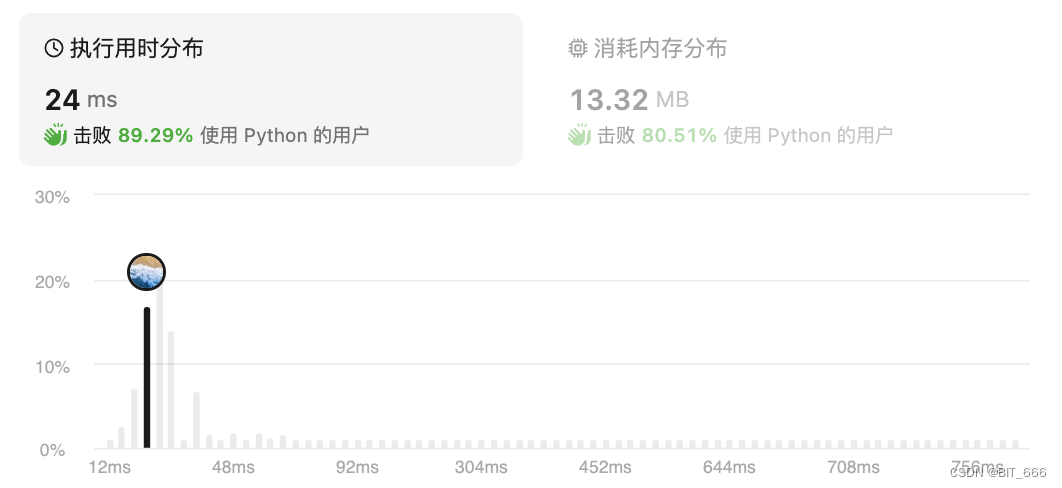
class Solution(object):def myPow(self, x, n):""":type x: float:type n: int:rtype: float"""# x^0 == 1if n == 0:return 1.0if n == 1:return xif n == -1:return 1 / xhalf = self.myPow(x, int(n / 2))rest = self.myPow(x, n % 2)return half * half * rest

half 负责将 2^n 减半，rest 负责检查是否需要补充一个 2。

5.N-Queen [51]

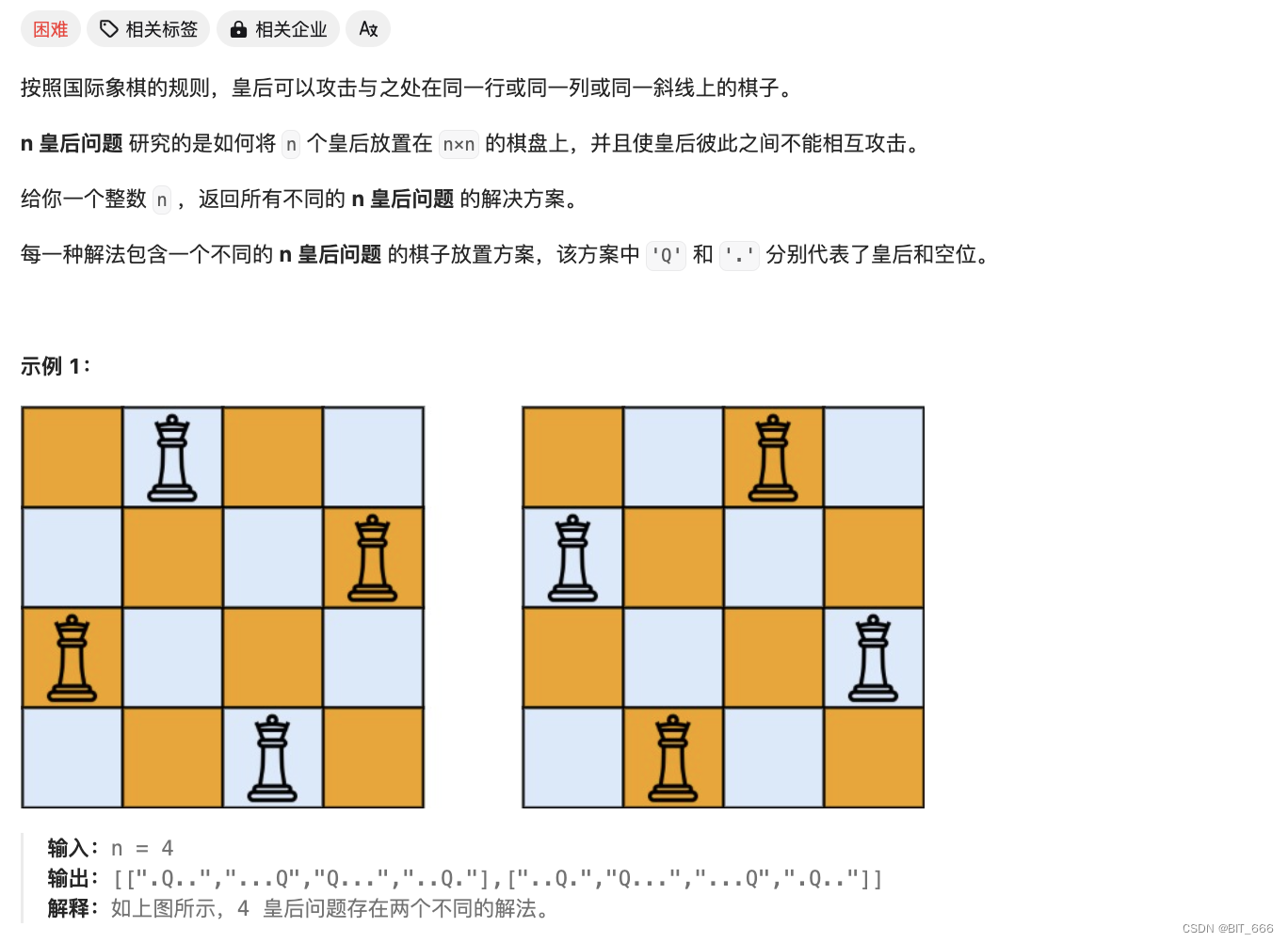
N 皇后: https://leetcode.cn/problems/n-queens/description/

◆ 题目分析

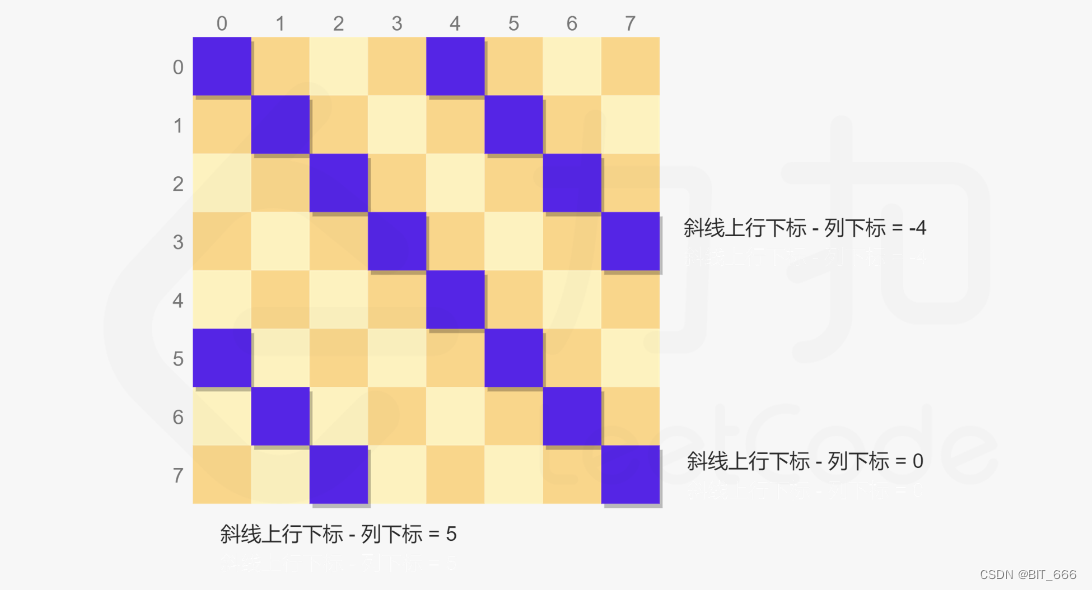
给定 n x n 的棋盘放置皇后，要求其上下左右和对角线都不可以放置其他皇后，观察棋盘坐标，我们可以发现是否同一行同一列比较简单，row / col 相等即可，对于左右 45° 的对角线，我们可以通过 row col 组合获取，这里我们称为撇 pie 和捺 na，pie 上的元素 row + col 都相同，na 上的元素 row - col 都相同，这样通过 row、col 我们即可判断所有可行的情况，剩下递归即可。

◆ 回溯实现

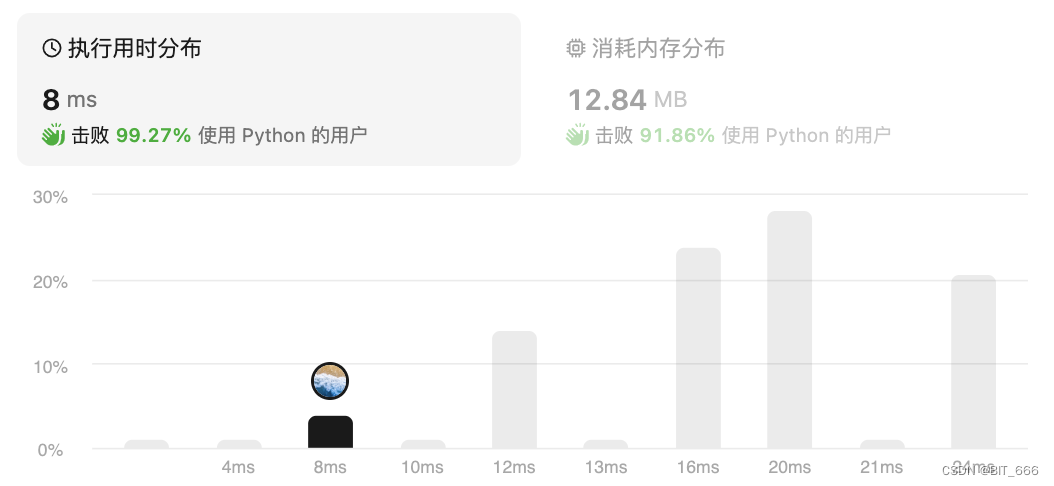
class Solution(object):def solveNQueens(self, n):""":type n: int:rtype: List[List[str]]"""results = []# 行 左 右 是否可以放置cols = set()pie = set()na = set()def dfs(n, row, cur):if row >= n:results.append(cur)for col in range(n):if col in cols or (row + col) in pie or (row - col) in na:continue# 判断有效cols.add(col)pie.add(row + col)na.add(row - col)dfs(n, row + 1, cur + [col])# 恢复状态cols.remove(col)pie.remove(row + col)na.remove(row - col)dfs(n, 0, [])return self.genResult(n, results)def genResult(self, n, results):return [[ '.' * i + 'Q' + (n - i - 1) * '.' for i in result] for result in results]def genResultV2(self, n, results):re = []for result in results:re.append([ '.' * i + 'Q' + (n - i - 1) * '.' for i in result])return re

这里最后获取 results 后还需要给出棋盘的形态，所以我们需要根据索引构建 '.' 和 'Q' 的关系。

6.Combinations [78]

组合: https://leetcode.cn/problems/combinations/description/

◆ 题目分析

固定第一个数字，向后遍历其他结果，待数量达到 k 停止，再回溯，固定下一个数字，向后寻找结果，直到 n-k 时再循环一次结束。

◆ 回溯实现

class Solution(object):def combine(self, n, k):res = []self.get_combine(res, [], n, k, 1)return resdef get_combine(self, res, prefix, n, k, start):if k == 0:# K 个结果找到了res.append(list(prefix))elif start <= n:# 添加当前结果prefix.append(start)# 添加完 start , 还需要 k-1 个, start + 1 去重self.get_combine(res, prefix,n, k - 1, start + 1)# 恢复状态，还需要 k 个，从 start + 1 开始prefix.pop()self.get_combine(res, prefix,n, k, start + 1)

其运行过程可以参考下图，固定 1 之后，start_index 一直向后查找添加 [1, 2]、[1, 3]、[1, 4] 后，start_index 为 5，[1] 结束，pop 得到 []，start_index + 1，再固定 2 从 2 开始 ...

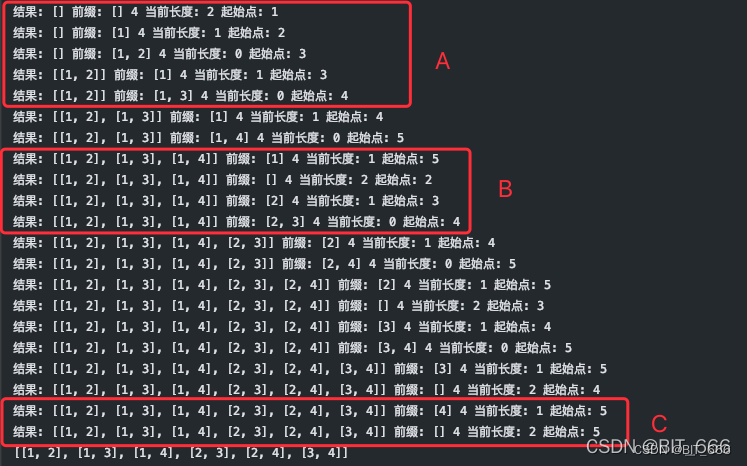
◆ 树形结合

class Solution(object):def combine(self, n, k):res = []com = []def backtracking(n, k, start_index):if len(com) == k:res.append(com[:])return # 因为全排列不包含 0，所以最后 + 1for num in range(start_index, n + 1):com.append(num)backtracking(n, k, num + 1) # 递归com.pop() # 回溯backtracking(n, k, 1)return res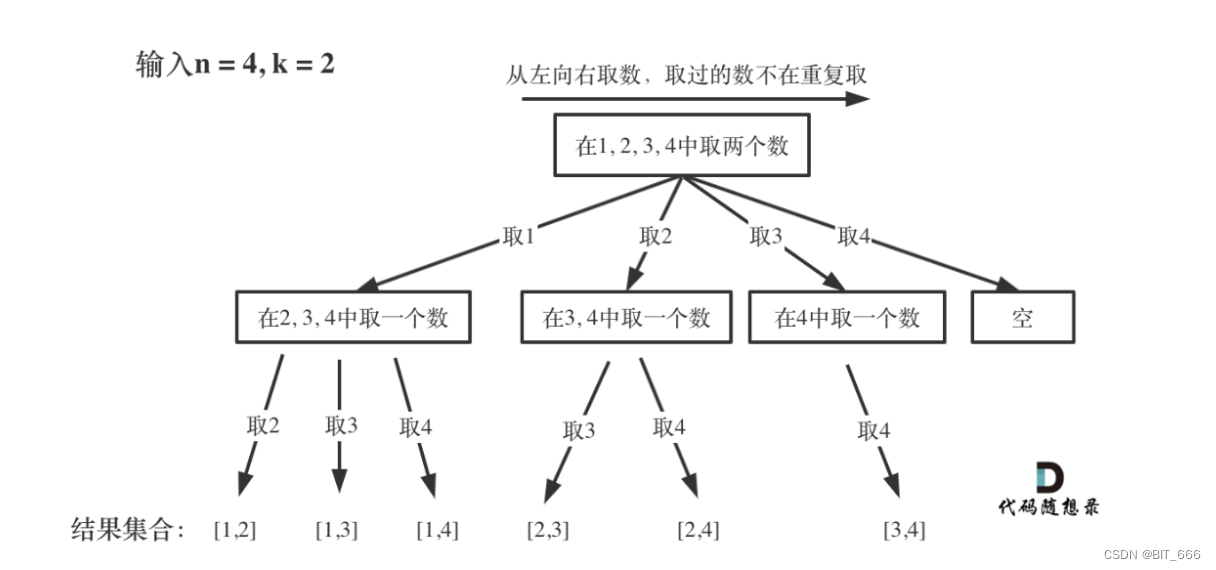

每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围。

图中可以发现 n 相当于树的宽度，k 相当于树的深度，代码遵照下述思路完成。

◆ 剪枝优化

class Solution(object):def combine(self, n, k):res = []com = []def backtracking(n, k, start_index):if len(com) == k:res.append(com[:])return last_index = n - (k - len(com)) + 1# 因为全排列不包含 0，所以最后 + 1for num in range(start_index, last_index + 1):com.append(num)backtracking(n, k, num + 1) # 递归com.pop() # 回溯backtracking(n, k, 1)return res

本题还可以通过剪枝进行优化，对于遍历而言，当 n=4、k=2 时，我们就没有必要再从 4 开始遍历了，因为后面已经不足以拼到 2 个数字了，所以我们优化一下循环的次数 n - (k - len(com)) + 1。

7.Sub-Sets [78]

子集: https://leetcode.cn/problems/subsets/description/

◆ 题目分析

遍历多种情况，假设 [1, 2, 3]，我们可以先遍历 [1] 生成所有情况，再遍历 [2] 和之前的情况结合并添加，随后继续，每次结果都会翻倍，因为新的数字会和之前的每个结果生成一个新的结果并添加。

◆ 循环实现

class Solution(object):def subsets(self, nums):""":type nums: List[int]:rtype: List[List[int]]"""res = [[]]# 遍历每个数字for i in nums:res = res + [[i] + re for re in res]return res

8.Majority-Element [169]

多数元素: https://leetcode-cn.com/problems/majority-element/description/

◆ 题目分析

第一感觉是 wordcount 直接判断即可，但是既然出在回溯和分治的章节，说明其还有其他方法，我们两种方法尝试下。

◆ 字典计数

class Solution(object):def majorityElement(self, nums):""":type nums: List[int]:rtype: int"""limit = len(nums) / 2count = {}for i in nums:if i not in count:count[i] = 0# 判断是否超过 n/2if count[i] + 1 > limit:return ielse:count[i] += 1return 0

计数判断即可。

◆ 分治实现

class Solution:def majorityElement(self, nums):def backtrack(lo, hi):# base case; the only element in an array of size 1 is the majority# element.if lo == hi:return nums[lo]# recurse on left and right halves of this slice.mid = (hi - lo) // 2 + loleft = backtrack(lo, mid)right = backtrack(mid + 1, hi)# if the two halves agree on the majority element, return it.if left == right:return left# otherwise, count each element and return the "winner".left_count = sum(1 for i in range(lo, hi + 1) if nums[i] == left)right_count = sum(1 for i in range(lo, hi + 1) if nums[i] == right)return left if left_count > right_count else rightreturn backtrack(0, len(nums) - 1)

如果数 a 是数组 nums 的众数，如果我们将 nums 分成两部分，那么 a 必定是至少一部分的众数，所以题目将数组不断拆分，并获取两个部分的众数，这里不是太推荐使用分治法，因为这个场景复杂度太高。