1、线性回归概述

线性回归（Linear Regression）是很基础的机器学习算法。线性回归在机器学习知识结构中的位置如下：

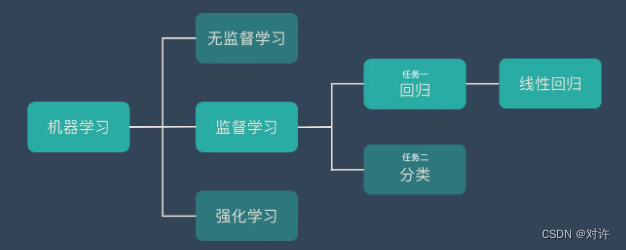
1.1、什么是回归

回归（Regression）是一种应用广泛的预测建模技术，这种技术的核心在于预测的结果是连续型变量

回归是监督学习中的一个重要问题，用于预测输入变量（自变量）和输出变量（因变量）之间的关系，特别是当输入变量的值发生变化时，输出变量的值随之发生的变化，回归模型正是表示从输入变量到输出变量之间映射的函数

其中，自变量表示主动操作的变量，可以看做因变量的原因。因变量因为自变量的变化而变化，可以看做自变量的结果

回归问题的学习等价于函数拟合：选择一条函数曲线，使其很好地拟合已知数据且很好地预测未知数据

回归的目的是为了预测，比如预测明天的天气温度，预测股票的走势…

回归之所以能预测是因为他通过历史数据，摸透了“套路”，然后通过这个套路来预测未来的结果

1.2、什么是线性

“越…，越…”，符合这种说法的就可能是线性个关系，例如，房子越大，价格就越高

但是并非所有“越…，越…”都是线性的，例如，“充电越久，电量越高”，它就类似下面的非线性曲线：

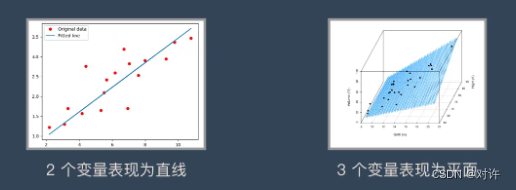
线性关系不仅仅只能存在2个变量（二维平面）。3个变量时（三维空间），线性关系就是一个平面，4个变量时（四维空间），线性关系就是一个体。以此类推…

1.3、什么是线性回归

线性回归本身是统计学里的概念，现在经常被用在机器学习中

在统计学中，线性回归（Linear Regression）是利用称为线性回归方程的最小平方和函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析，这种函数是一个或多个被称为回归系数的模型参数的线性组合 。只有一个自变量时称为简单回归，大于一个自变量时称为多元回归

如果2个或者多个变量之间存在“线性关系”，那么我们就可以通过历史数据，摸清变量之间的“套路”，建立一个有效的模型，来预测未来的变量结果

1.4、线性回归的优缺点

优点：

• 建模速度快，不需要很复杂的计算，在数据量大的情况下依然运行速度很快
• 可以根据系数给出每个变量的理解和解释

缺点：

• 不能很好地拟合非线性数据。所以需要先判断变量之间是否是线性关系

为什么在深度学习大杀四方的今天还使用线性回归呢？

一方面，线性回归所能够模拟的关系其实远不止线性关系。线性回归中的“线性”指的是系数的线性，而通过对特征的非线性变换，以及广义线性模型的推广，输出和特征之间的函数关系可以是高度非线性的。另一方面，也是更为重要的一点，线性模型的易解释性使得它在物理学、经济学、商学等领域中占据了难以取代的地位

1.5、线性回归与逻辑回归

线性回归和逻辑回归是2种不同的经典算法。经常被拿来做比较，下面整理了一些两者的区别：

项目	解决问题类型	变量类型	线性关系	表达变量关系
线性回归	回归	连续	符合线性关系	直观表达变量关系
逻辑回归	分类	离散	可以不符合线性关系	无法直观表达变量关系

• 线性回归只能用于回归问题，逻辑回归虽然名字叫回归，但是更多用于分类问题（关于回归与分类的区别参考文章：传送门）
• 线性回归要求因变量是连续性数值变量，而逻辑回归要求因变量是离散的变量
• 线性回归要求自变量和因变量呈线性关系，而逻辑回归不要求自变量和因变量呈线性关系
• 线性回归可以直观的表达自变量和因变量之间的关系，逻辑回归则无法表达变量之间的关系

2、线性回归的原理

2.1、线性回归的定义与原理

线性回归的定义及原理推导详见文章：传送门

2.2、线性回归的损失函数

损失函数（Loss Function），也称成本函数（Cost Function），描述的是模型的预测值与真实值的差异，并将这种差异映射为非负实数以表示模型可能带来的“风险”或“损失”。机器学习中将损失函数作为模型拟合好坏的评判准则，并通过最小化损失函数求解和评估模型

在多元线性回归中，其损失函数定义如下：
$$L=\sum _{i=1}^m(y_i-f(x$$