C4996    'fopen': This function or variable may be unsafe. 
Consider using fopen_s instead. To disable deprecation, 
use _CRT_SECURE_NO_WARNINGS. See online help for details.

在工程文件处右击，选择属性->配置属性->C/C++->预处理器

 

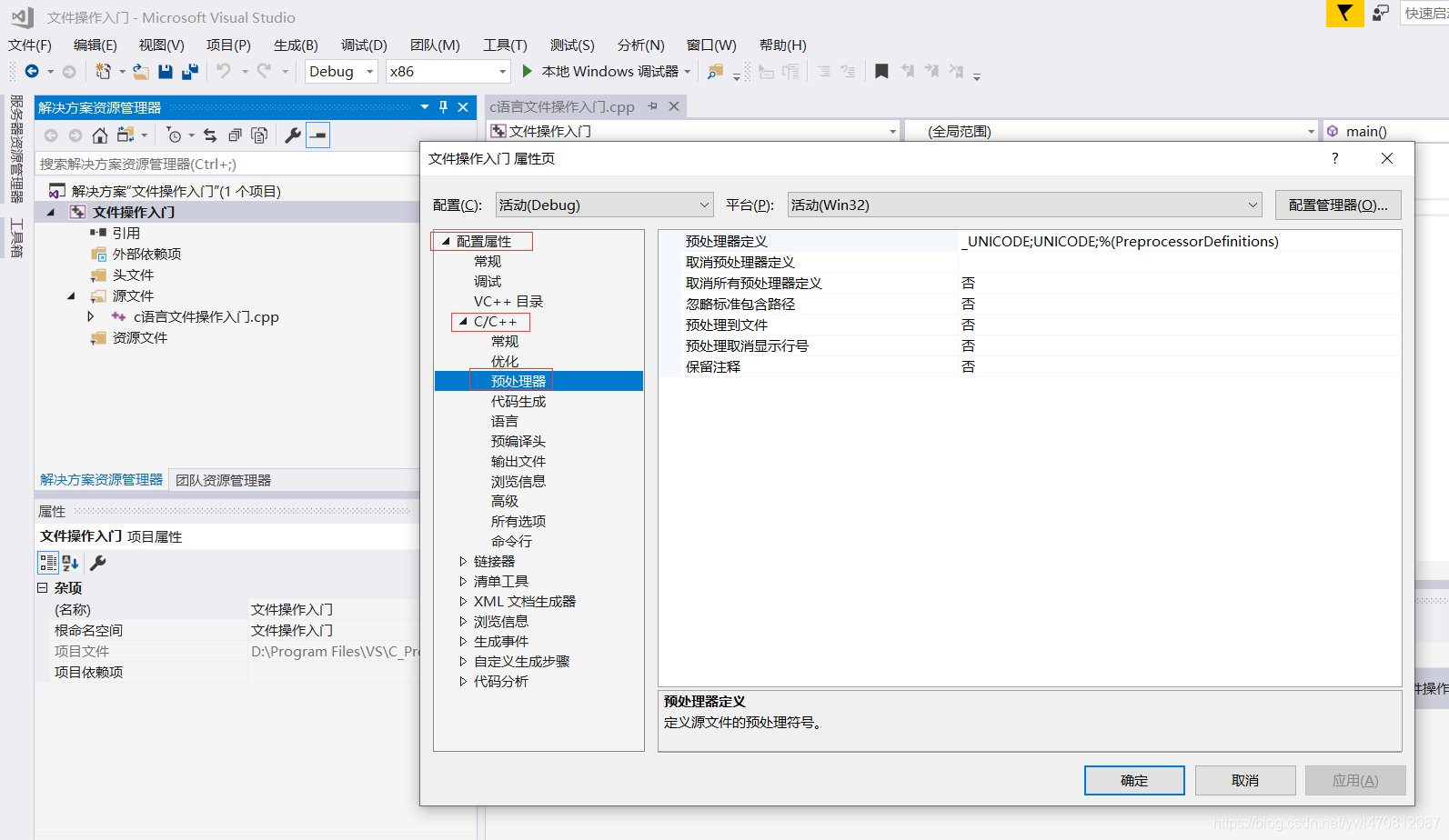
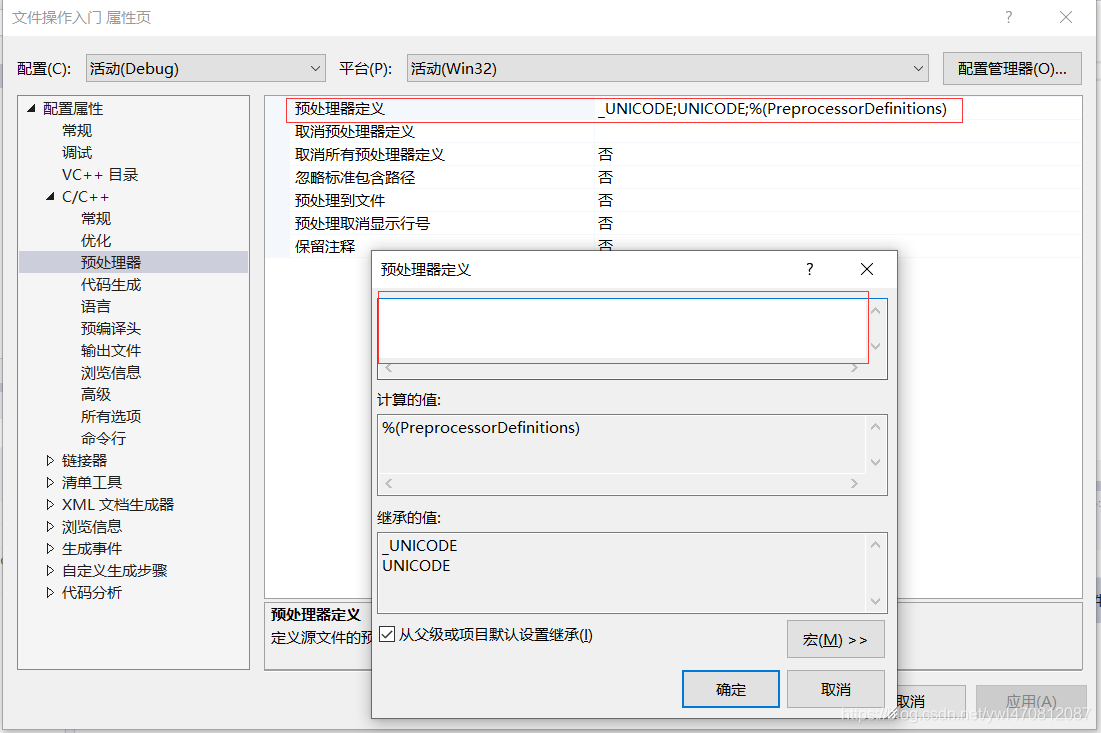
加入一个_CRT_SECURE_NO_WARNINGS

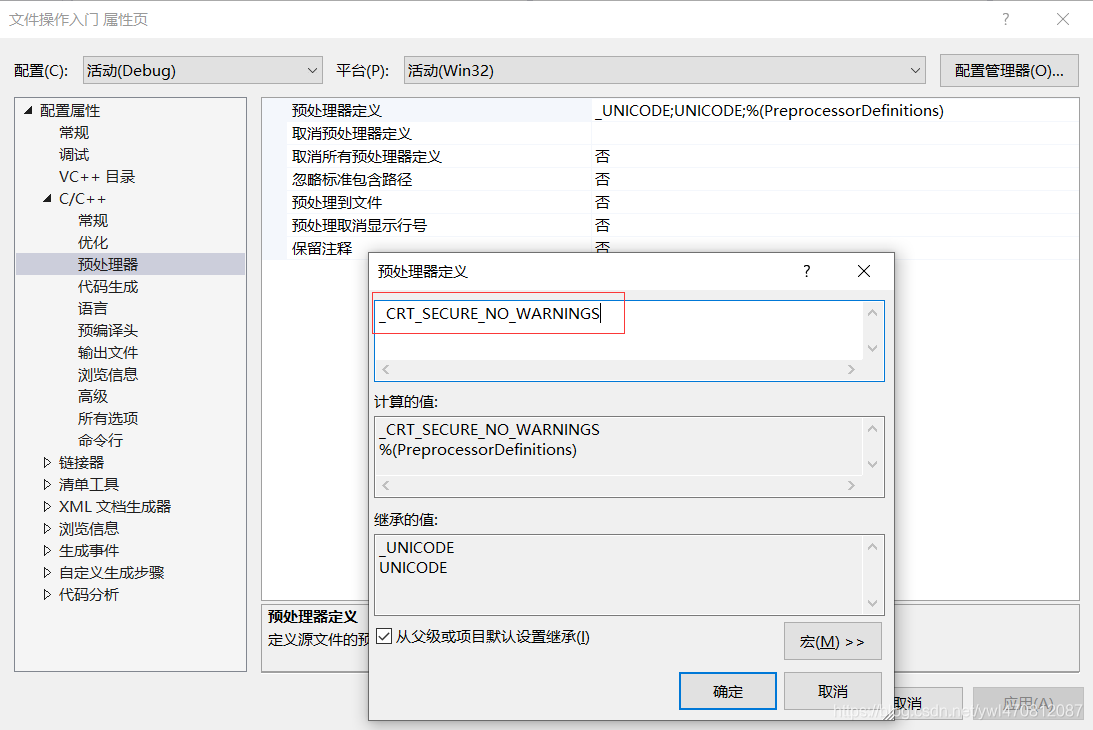
运行代码

#include <stdio.h>int main() {FILE *fp;char buf[20];fp=fopen("D:\\1.txt", "r");if (NULL == fp) {printf("打开文件失败");}fgets(buf, 20, fp);printf("%s", buf);fgets(buf, 20, fp);printf("%s", buf);fgets(buf, 20, fp);printf("%s", buf);fclose(fp);while (true){}
}

 

运行结果

 

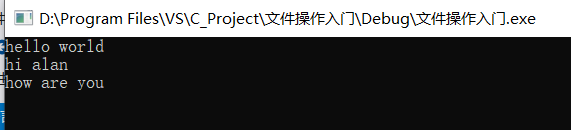
完美解决