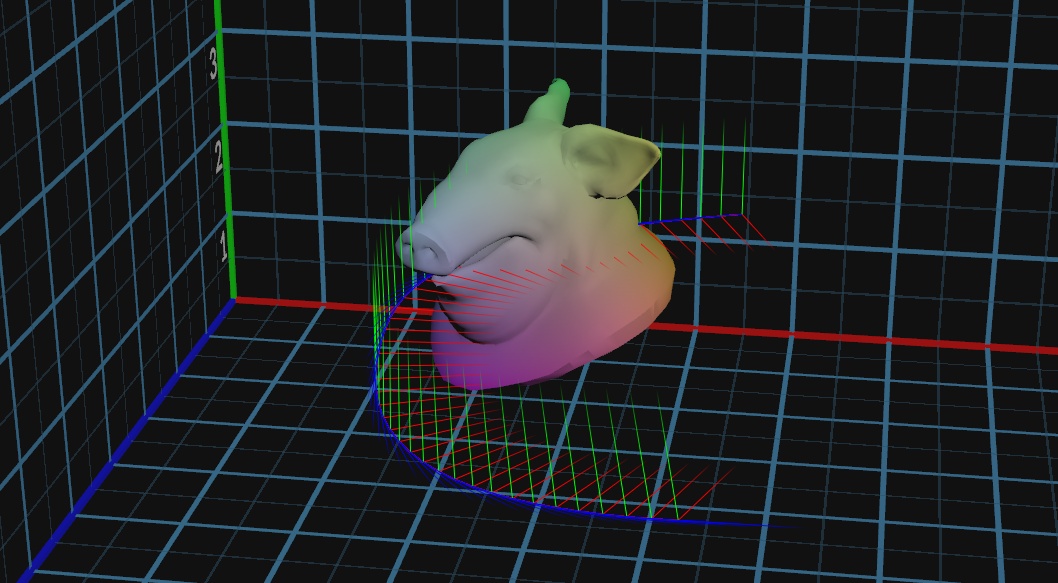
设想:
先从二维上来看直角坐标系。物体是由x,y两个轴向的数据组成的。少了其中一组数据物体就只能是分布在单一轴向上的点。
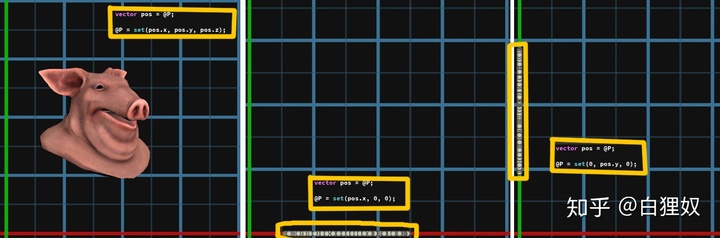
现在将x、y加起来,可见在三维空间中形成了一个平面。

从目前的情况上来看我们已经知道了后续再添加上z轴信息的物体情况。
因为坐标系是三个完全交叉相互垂直的平面,所以当只有两个轴向信息时物体只能组成一个平面。当我们添加第三个轴向时,物体开始突破平面变成三维物体。
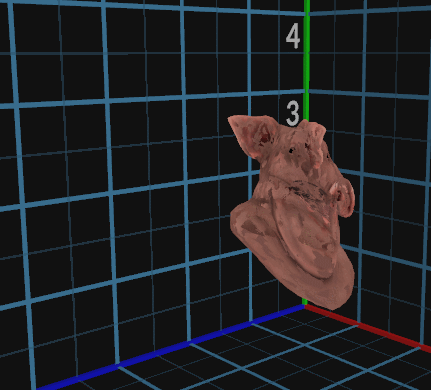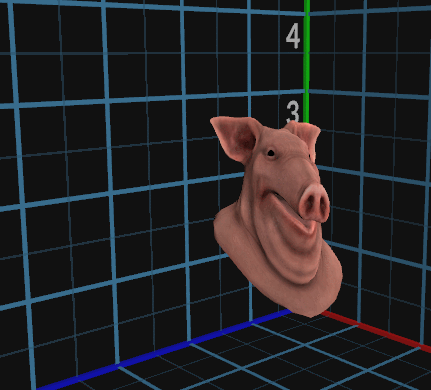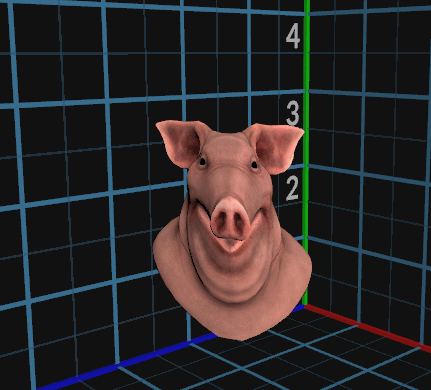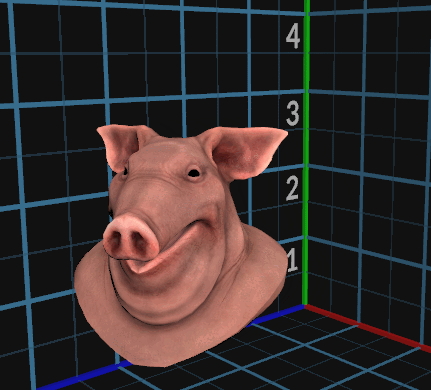
以上,我们还原了物体的三维构建。
由此可以得到,三维物体组成的公式为:
P = ( P.x , 0, 0)+ ( 0, P.y, 0) + ( 0, 0, P.z);
在最后的动图中我们可以看到,物体加上z轴的向量的时候时笔直的朝着Z轴方向进行增加。
前面讲述过三个轴是相互垂直的,现在P.z上面储存的值是小数,且位于向量第三个位置,所以相对于是加上了(0,0,z),物体不会在x、y上面出现变化。
这就是这篇文章的重点,既然因为坐标系是直角,所以还原物体数据时只会相互垂直的相加形成,那我们把第三个轴向变形扰乱会怎样呢?物体是否就会因此而变形?
一、重映射曲线位置到模型。
想单独给物体的z轴添加信息首先需要保存一个物体的bound box局部的相对位置关系来记录物体的点排布顺序。

vector max, min;
getbbox(min, max);vector transZero = {0,0,0} - min; vector localP = @P + transZero; //Translate Object to coordinate origin.vector boundSize = max - min;
vector bbox = localP / boundSize;@Cd = bbox;
v@bbox = bbox;曲线是有uv的,曲线上uv一般为(u,0.5),v向是没有数值的,这个u值记录了类似物体boundbox一样的0-1参数。
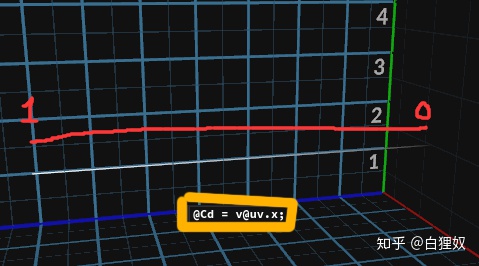
使用Geo的boundBox.z的0-1去匹配上曲线uv.u的0-1得到新的物体Z轴向量。
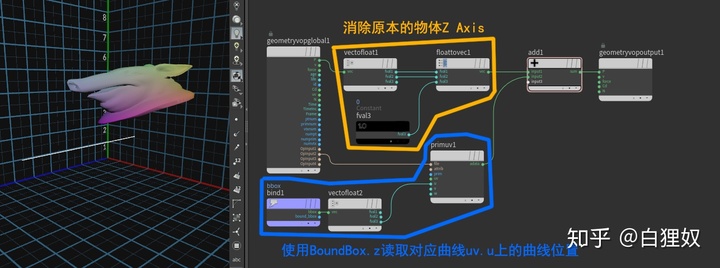

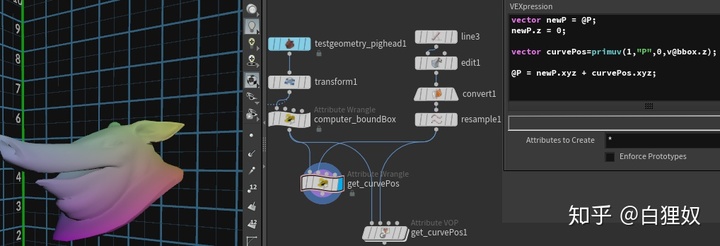
vector newP = @P;
newP.z = 0;vector curvePos=primuv(1,"P",0,v@bbox.z);@P = newP.xyz + curvePos.xyz;二、效果修正
上述基本上已经完成了曲线变形的制作思路,但是还会涉及比较具体的一些问题没有讲到:
1.物体没有匹配到曲线上。
2.物体没有读取变形的旋转信息值读取了Position,没有rotate矩阵。
3.物体变形拉伸。
4.物体位移。
1.物体现在离曲线有一定的差距
因为不光在z轴加了curvePos,在xy轴也加上了curvePos,物体变形后的位置是本身对于original的位置再机上curvePos对于original的位置。
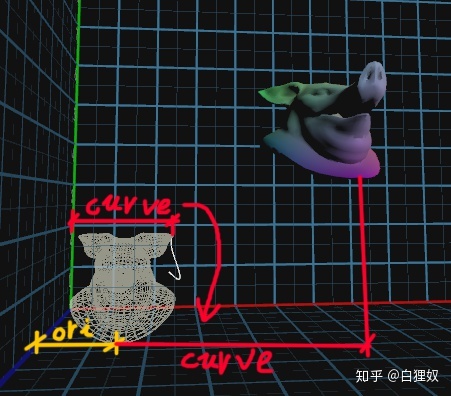
解决方法很简单,把物体归零就好,然后物体的朝向一直设定为旋转到z轴(自己想想怎么做)。
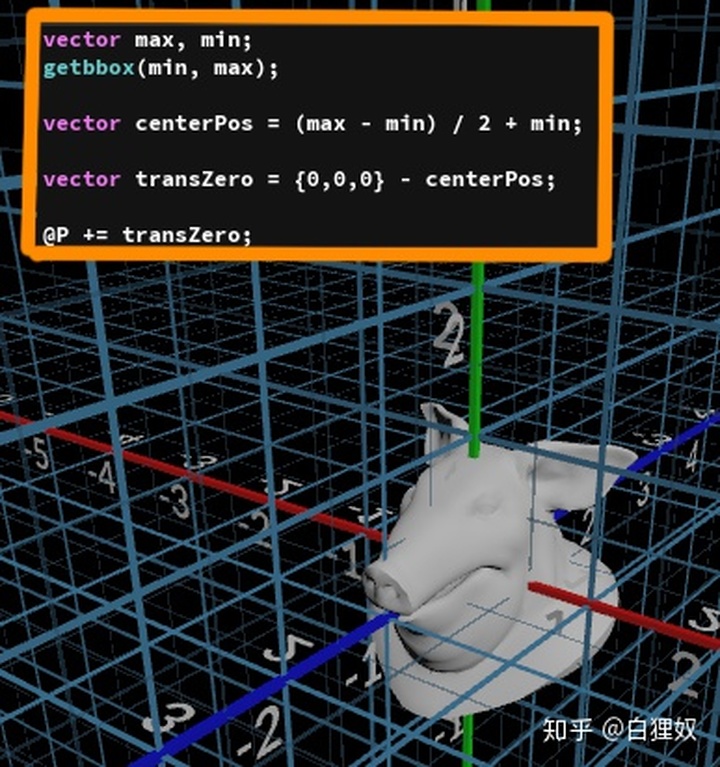
2.曲线的旋转信息
在编辑曲线使其弯曲后,发现物体对于弯曲的曲线只是在x轴向上进行了变化,是直直的向其他方向位移过去的,并没有弯曲变形的感觉。

因此需要用到上一篇文章说得那样,给点定义一个自身的矩阵记录旋转信息。
这里我们用lookat函数来制作。
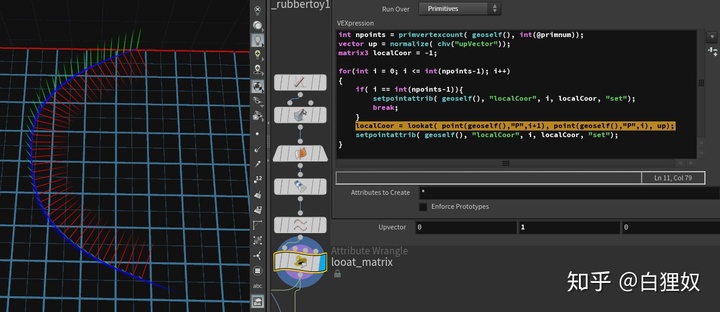
int npoints = primvertexcount( geoself(), int(@primnum));
vector up = normalize( chv("upVector"));
matrix3 localCoor = -1;for(int i = 0; i <= int(npoints-1); i++)
{if( i == int(npoints-1)){setpointattrib( geoself(), "localCoor", i, localCoor, "set");break;}localCoor = lookat( point(geoself(),"P",i+1), point(geoself(),"P",i), up); setpointattrib( geoself(), "localCoor", i, localCoor, "set");
}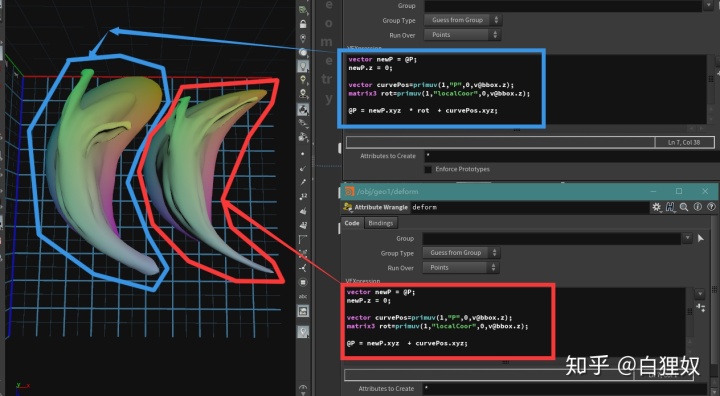
加上了旋转后,整个物体的变形才是正确的。
3.物体拉伸
因为直接用boundBox的0-1去适配长度不相同的曲线的uv0-1所以必然会出现拉伸。其实解决方法也很简单,用物体变形轴(Z Axis)的长度 / 曲线长度得到他们的缩放因子,乘以 boundBox.z。
newBbox = bbox * ( boundSize.z / curveLength);
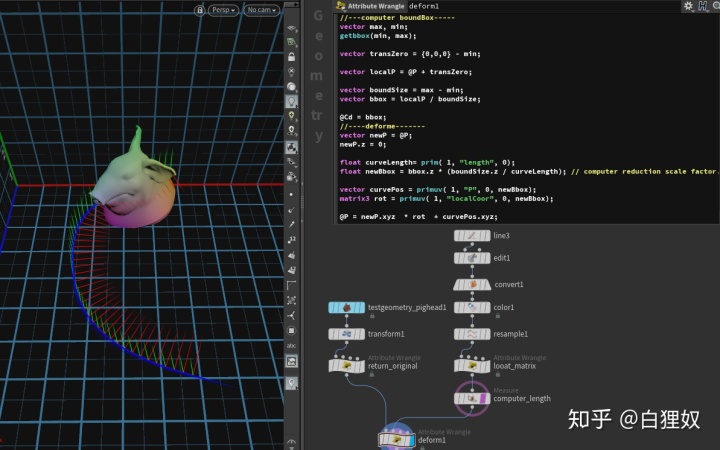

//---computer boundBox-----
vector max, min;
getbbox(min, max);vector transZero = {0,0,0} - min;vector localP = @P + transZero;vector boundSize = max - min;
vector bbox = localP / boundSize;@Cd = bbox;
//----deforme-------
//remap bbox.
float curveLength= prim( 1, "length", 0);
float newBbox = bbox.z * (boundSize.z / curveLength); // computer reduction scale factor.vector newP = @P;
newP.z = 0;vector curvePos = primuv( 1, "P", 0, newBbox);
matrix3 rot = primuv( 1, "localCoor", 0, newBbox);@P = newP.xyz * rot + curvePos.xyz;4.物体位移
通过上面的缩放操作我们已经可以明白,想要控制物体在曲线上的缩放、位移,其实就是对于bbox值的一个重映射,缩放是*一个factor进行保持原物体0-1整个范围值内关系的映射。位移则是+上一个数值,进行整体的位移(这些都可以也可以使用在去曲线上不同的值去进行计算)。
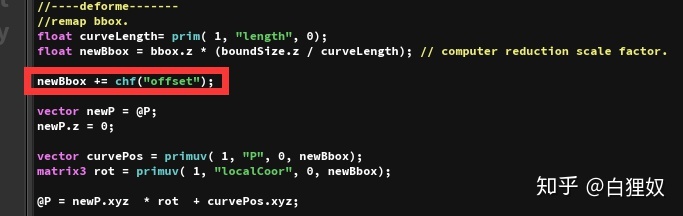
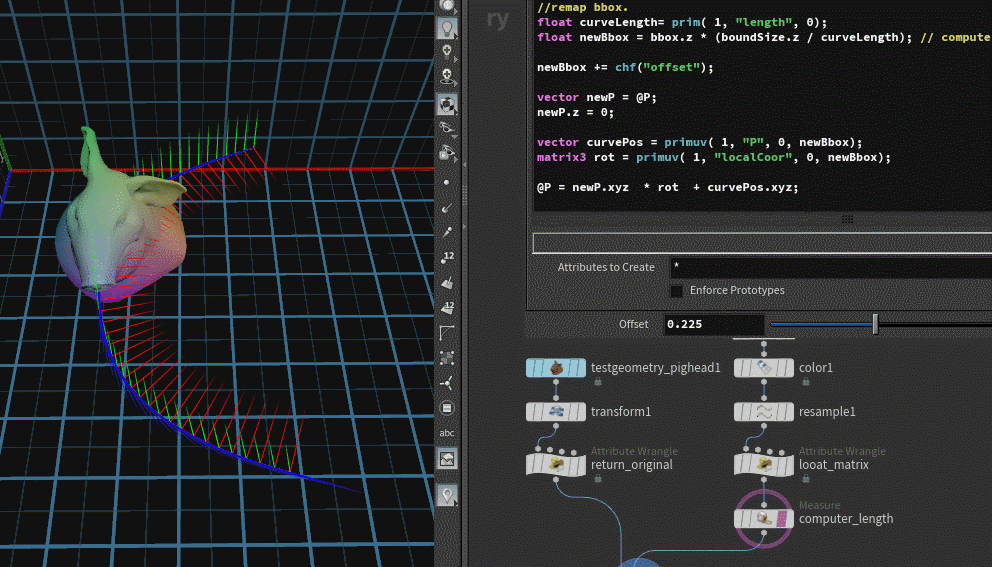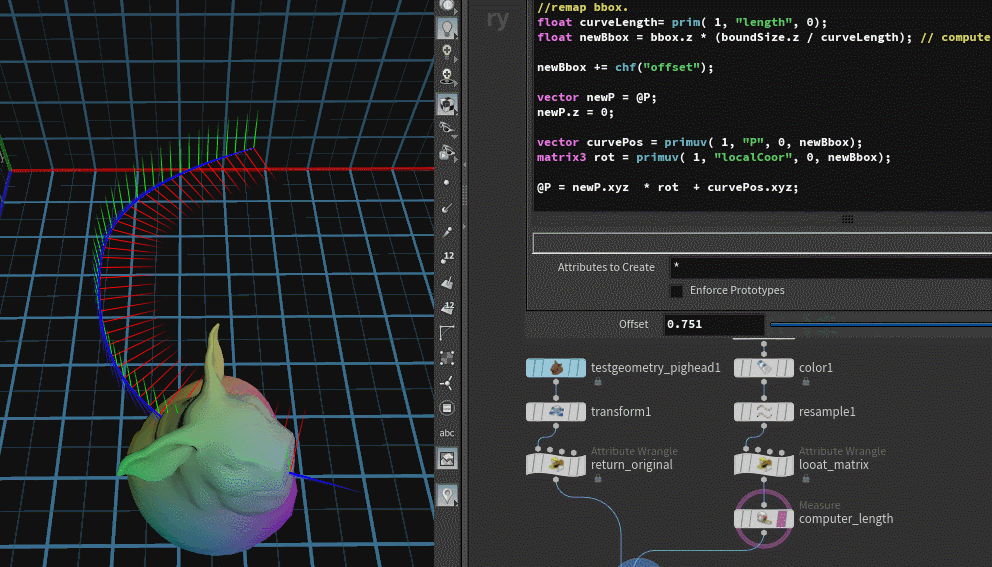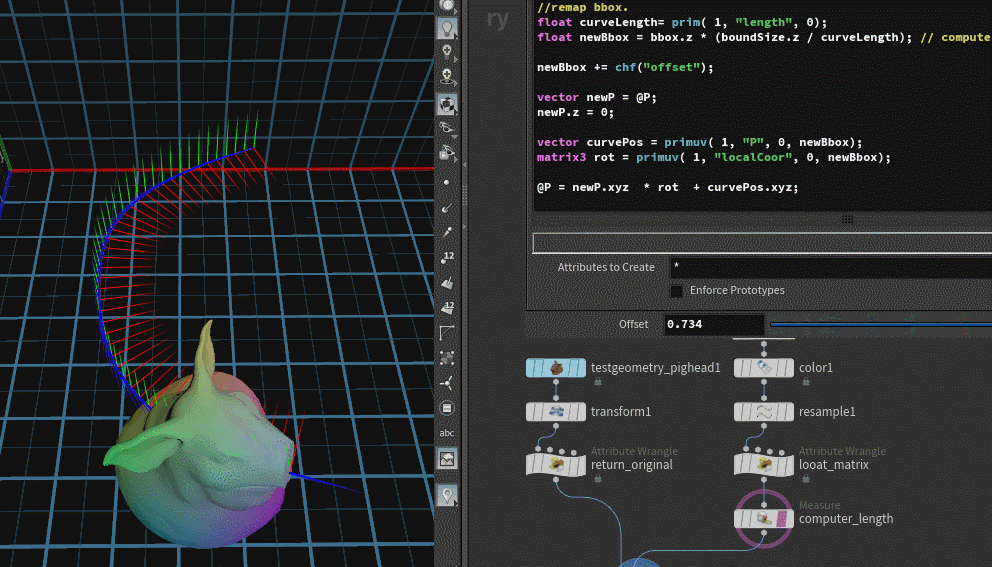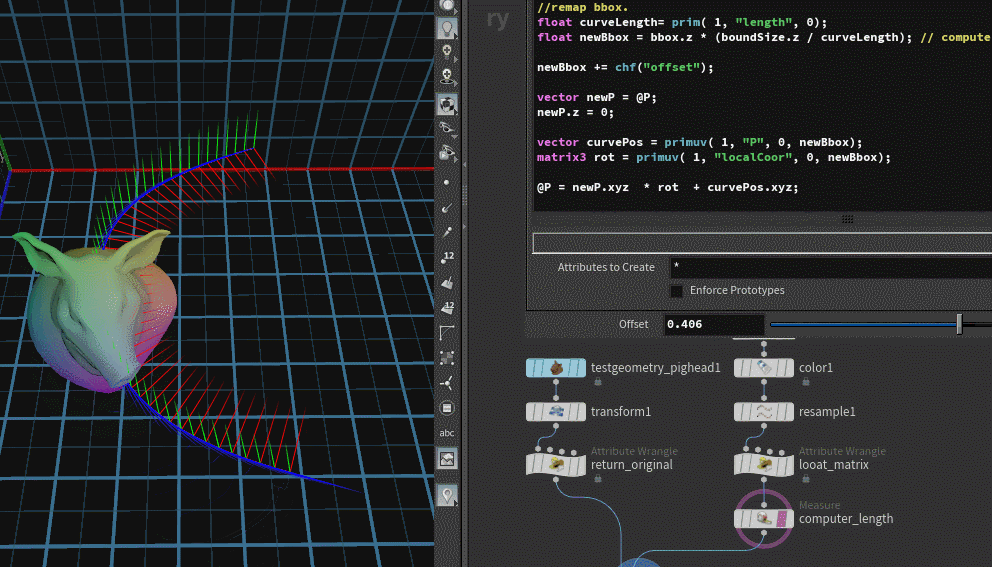
最终代码
//---computer boundBox-----
vector max, min;
getbbox(min, max);vector transZero = {0,0,0} - min;vector localP = @P + transZero;vector boundSize = max - min;
vector bbox = localP / boundSize;@Cd = bbox;
//----deforme-------
//remap bbox.
float curveLength= prim( 1, "length", 0);
float newBbox = bbox.z * (boundSize.z / curveLength); // computer reduction scale factor.newBbox += chf("offset");vector newP = @P;
newP.z = 0;vector curvePos = primuv( 1, "P", 0, newBbox);
matrix3 rot = primuv( 1, "localCoor", 0, newBbox);@P = newP.xyz * rot + curvePos.xyz;总结:
以上基本实现了这个功能,其余的拓展功能(超过曲线的部分如何保持啊,怎么每个地方旋转不一样啊etc....)可以自己想想如何添加,基本上就是很简单的矩阵操作和逻辑问题。
Reference:
https://vimeo.com/247900360vimeo.com






)











