本文来讲一种搜索算法，即二分搜索算法，通常在面试时也会被问到。

我们先来看一个例子，在图书馆通常是根据查到的编号去找书，可以在书架上按顺序一本本地查找，也可以找到一本书不符合预期时，再跳过一大部分书再查找，很显然，后者的效率高，这也是大部分人使用的方法，这种方法叫做二分搜索查找方法。

二分搜索查找原理

二分搜索查找方法的核心思想是：在查找一次后将下一次搜索查找的空间减少一半，它要求搜索的序列值是单调的。如果序列是单调递增的，将查找目标值与序列的正中间值进行比较，如果相等则查找成功；如果查找目标值小于序列的正中间值，则下一次的搜索空间为正中间值的前面部分；如果查找目标值大于序列的正中间值，则下一次的搜索空间为正中间值得后面部分。如下图的数组

假如要查找元素8，那么先将8和数组中间的元素5进行比较，发现8比5大，那么下一次搜索空间为5后面的部分了，继续将后半部分的中间元素7与8进行比较，发现8比7大，那么下一次的搜索空间为7后面的部分了，再将7后面的中间元素8与8进行比较，发现相等，则查找成功。可以看出二分搜索查找算法的时间复杂度为O(log(n))。代码实现如下

int binary_search(int a[], int n, int x) { int left = 0; int rigt = n - 1; while(left < rigt) { int mid = (left + rigt) >> 1; if (a[mid] == x) { return x; } else if (a[mid] < x) { left = mid + 1; } else { rigt = mid - 1; } } return -1;}

二分搜索查找应用

为了更好地理解二分搜索查找算法，下面来看两个具体的应用。

1.给定一个正整数n，其中n小于10的8次方，求最小的正整数x，满足x的x次方为n位数。

先来看一个数x，它的位数怎么表示，很明显(int)log10(x) + 1就是表示x的位数，所以x的x次方的位数函数f(x)可以表示如下

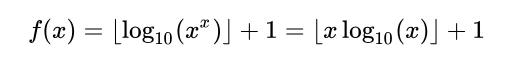
很明显，这个函数是一个单调递增函数，需要求最小的正整数x，满足f(x)=n，那么x只需要在10的8次方内进行二分查找搜索就好了。

2.给定一个正整数n，其中n小于等于10的18次方，求如下方程的正整数解

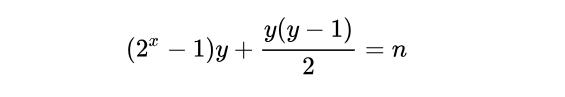
因为n最大为10的18次方，很明显那么x肯定不会超过60，所以x可以从1枚举到60，当x固定时，等号左边关于y的函数明显是一个单调增函数，所以可以用二分搜索查找法来求y了，时间复杂度为O(log(n))。

下一节我将会讲三分搜索方法的原理与应用，欢迎大家关注，谢谢。