python查询斐波那契数列通项公式_斐波那契数列求解总结（Python版）

最近在查阅斐波那契数列时，看到下面的文章，总结得非常好，于是自己上手使用 Python 练习并实现多种求解方法

守望：面试官问你斐波那契数列的时候不要高兴得太早zhuanlan.zhihu.com

斐波那契数列的定义：

斐波那契数列 又称黄金分割数列，指的是这样一个数列 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233，377，610，987，1597，2584，4181，6765，10946，17711，28657，46368........ 这个数列从第3项开始，每一项都等于前两项之和

根据定义递归求解

已知：Fib(0) = 0，Fib(1) = 1
Fib(n) = Fib(n-1) + Fib(n-2)

# 根据定义递归求解
def Fib_definition(n):# 检查输入if check_input(n):if (n <= 1): return nreturn Fib_definition(n - 1) + Fib_definition(n - 2)# 默认返回值else:return -1

递归求解，避免重复计算已经出现过的元素

我们都知道，根据定义递归求解，会存在大量的重复计算，于是我们将已经计算过的值保存在数组里，这样在后续需要计算时可以直接使用已经计算过的值，避免重复计算

# 递归求解，避免重复计算已经出现过的元素
def Fib_definition_notRepeat(n, fib_arr = [0, 1]):if check_input(n):# 检查输入if n < 2: return fib_arr[n]else:# 填充数组for x in range(n):fib_arr.append(-1)# 当求得 fib_arr[n-1] 时，fib_arr[n-2] 已知fib_arr[n] = Fib_definition_notRepeat(n-1, fib_arr) + fib_arr[n-2]return fib_arr[n]else:# 默认返回值return -1

递推求解，从已知元素递推所求元素

根据定义递归求解，我们是根据需要求得的元素一步一步倒推，直到倒推到我们已知的元素 ( 第 0 个，第 1 个 )，属于“反向”计算，那如果“正向”计算，从已知元素递推所求元素呢？

# 递推求解，从已知元素递推所求元素
def Fib_recurrence(n):# 检查输入if check_input(n):if n < 2:return nelse:index = 2fib_index_pre_pre = 0fib_index_pre = 1fib_index = 0while n >= index:fib_index = fib_index_pre_pre + fib_index_prefib_index_pre_pre = fib_index_prefib_index_pre = fib_indexindex += 1return fib_indexelse:# 默认返回值return -1

递推求解，把已求得的元素放入数组中

def Fib_recurrence_arr(n):# 检查输入if check_input(n):if n < 2: return nelse:index = 2fib_arr = [0, 1]while n >= index:fib_arr.append(fib_arr[index-1] + fib_arr[index-2])index += 1return fib_arr[len(fib_arr)-1]else:# 默认返回值return -1

尾递归求解

如果不是很理解尾递归，请参见

什么是尾递归？www.zhihu.com

# 尾递归求解
def Fib_tail_recursion(n, index, fib_pre_pre, fib_pre):# 检查输入if check_input(n):if n < 2: return nelse:if n >= index:fib_index = fib_pre_pre + fib_prefib_pre_pre = fib_prefib_pre = fib_indexindex += 1return Fib_tail_recursion(n, index, fib_pre_pre, fib_pre)else: return fib_preelse:# 默认返回值return -1

利用矩阵求解，所求元素为

中的 A[0][0], 或

中的 A[0][1]

由于以下式子变形后满足定义

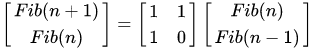
# 两个n阶矩阵相乘
def matrix_multiplication(n, A, B):C = []for line in range(n):line_arr = []for column in range(n):item = 0for i in range(n):item += A[line][i] * B[column][i]line_arr.append(item)C.append(line_arr)return C# 矩阵求解，所求元素为A^{n-1} 中的 A[0][0], 或 A^n 中的 A[0][1]
def Fib_matrix(n):if check_input(n):# 检查输入if n < 2: return nA = [[1, 1], [1, 0]]result = [[1, 0], [0, 1]]matrix_n = 2while n > 0:result = matrix_multiplication(matrix_n, result, A)n -= 1return result[0][1]else:# 默认返回值return -1

矩阵快速幂求解，所求元素为

中的 A[0][0], 或

中的 A[0][1]

利用快速幂算法缩短计算次数

# 两个n阶矩阵相乘
def matrix_multiplication(n, A, B):C = []for line in range(n):line_arr = []for column in range(n):item = 0for i in range(n):item += A[line][i] * B[column][i]line_arr.append(item)C.append(line_arr)return C# 矩阵快速幂求解，所求元素为A^{n-1} 中的 A[0][0], 或 A^n 中的 A[0][1]
def Fib_matrix_power(n):# 检查输入if check_input(n):if n < 2: return nA = [[1, 1], [1, 0]]result = [[1, 0], [0, 1]]matrix_n = 2while n > 0:# 判断最后一位是否为1，即可知奇偶if n & 1:result = matrix_multiplication(matrix_n, result, A)A = matrix_multiplication(matrix_n, A, A)n //= 2# n = n >> 1return result[0][1]else:# 默认返回值return -1

通项公式求解

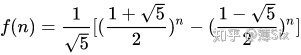
详细推导过程可参考：

斐波那契数列为什么那么重要，所有关于数学的书几乎都会提到？www.zhihu.com

# 通项公式求解
import numpy
import math
def Fib_general_formula(n):denominator = math.sqrt(5)return int((numpy.power((1+denominator)/2, n) - numpy.power((1-denominator)/2, n)) / denominator)

利用Python生成器

因为这个不是所有语言都能够使用，所以我放在了最后

# 利用 Python 生成器求解
def Fib_python_generator(n):a, b = 0, 1while n > 0:a, b = b, a + bn -= 1yield a
# 获取生成器的最后一个元素
def get_python_generator_item(n):item = 0for i in Fib_python_generator(n):item = ireturn item