前阵子,有小伙伴在我B站的算法教程底下留言

小伙伴们有任何疑问或者希望我解说任何内容,都可以在我的小我私家B站或民众号(xmg_mj)留言哦,我会尽我最大能力、只管抽时间去写文章\录视频来回应人人。
关于快速幂
实在快速幂相关的问题,是加入算法竞赛(NOI、ACM等)的小伙伴必须要掌握的一小块基础内容。固然,就算你不设计加入算法竞赛,小我私家以为只要你是一名程序员,就必须要掌握快速幂算法。
在《计算机程序设计艺术》一书中就有提到快速幂算法,此书的英文名是The Art of Computer Programming,简称TAOCP。

TAOCP出自Donald Ervin Knuth先辈之手。Knuth先辈是在计算机领域成就颇丰的着名科学家,是著名的KMP算法的发明人之一,在1974年获得“计算机领域的诺贝尔奖”:图灵奖(昔时他才36岁)。现在TAOCP已经出书了第1、2、3、4A卷,凭据设计,另有第4B、5、6、7卷未出书。第一卷首发于1968年,Knuth先辈今年是82岁高寿,听说他设计在105岁之前完成这部巨著。

关于TAOCP,微软创始人Bill Gates曾说过
If you think you’re a really good programmer… read (Knuth’s) Art of Computer Programming… You should definitely send me a resume if you can read the whole thing.
也许意思是:若是你以为自己是一位异常优异的程序员,那就应该阅读Knuth的TAOCP;若是你能读懂全部内容,可以直接给我发送一份简历。听说Knuth先辈的言辞加倍犀利:看不懂就别当程序员了!不外TAOCP对于新手来说,阅读难度简直对照大,书中的所有示例都使用了Knuth先辈自创的MIX汇编语言。
阅读本文之前的提醒
今天就抽闲写一篇文章来解说一下经典的快速幂算法哈。不外要想彻底看懂本文,有几个前提条件
熟悉算法中的2个基础观点:时间复杂度、空间复杂度
若是你压根没听过这2个观点,说明你的算法基础完全为0,真的没有在开顽笑!
可以向民众号发送复杂度获取相关教程
熟悉二进制和十进制的转换
若是连这个都不熟悉的话,那你的编程基础就真的需要好好补补啦
可以向民众号发送进制获取相关教程
熟悉常见的位运算操作
n & 1的效果是n最低二进制位的值,也可以用于判断n的奇偶性
求正整数n / 2,可以用位运算取代:n >> 1
若是不明白上述操作的原理,可以向民众号发送位运算获取相关教程
什么是幂(Power)?
众所周知,x的n次幂,是指x的n次方,也就是n个x相乘,好比2的4次幂就是2 * 2 * 2 * 2。
为了简化形貌,后面x的n次幂,我就简化为x ^ n(本文中的 ^ 并不是按位异或的意思)
那若何通过编程求幂?假设只思量x、n是整数且n大于即是0的情形,最容易想到的方式如下所示(这里接纳的编程语言是Java,但没有涉及Java特殊的语法。以是就算你没用过Java,也可以看懂)
int power(int x, int n) {
int result = 1;
while (n-- > 0) {
result *= x;
}
return result;
}
很显然,这种方式的时间复杂度是O(n)、空间复杂度是O(1)
什么是快速幂?
所谓快速幂,就是用效率更高(时间复杂度更低)的方式求幂,可以将时间复杂度优化至O(logn)。这里先容2种求解方式:递归、非递归
递归
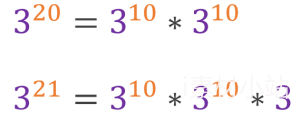
凭据上图中的等式,不难写出以下代码
int fastPower(int x, int n) {
if (n == 0) return 1;
int result = fastPower(x, n >> 1);
result *= result;
return (n & 1) == 0 ? result : result * x;
}
这个方式的时间、空间复杂度都是O(logn)。
那若何剖析出这个方式的复杂度呢?
若是你的算法功底对照微弱,可以代入特定值作一个也许的剖析,好比当n为16时,方式的递归挪用历程如下图所示

不难看出,每次挪用时,n的规模都减半,以是时间和空间复杂度都是O(logn)
若是你的算法功底还行,那就可以用更专业的方式去剖析它的复杂度(没有一定的算法基础,可能会看不懂)
这实在是典型的应用分治计谋的算法
假设T(n)是数据规模为n时的时间复杂度,不难得出递推式:T(n) = T(n / 2) + O(1)
最后凭据递推式 + 主定理(Master Theorem)可以直接得出结论:T(n) = O(logn)
非递归
我们以求3 ^ 21为例子,来剖析一下非递归的代码应该怎么写。
首先21的二进制形式是10101
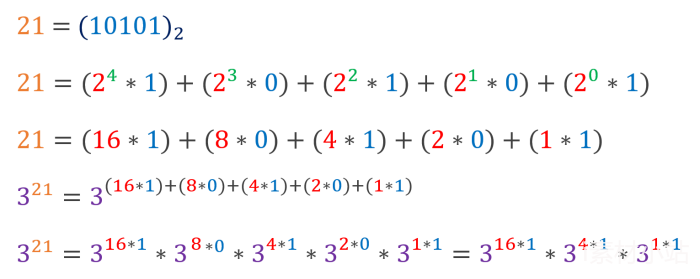
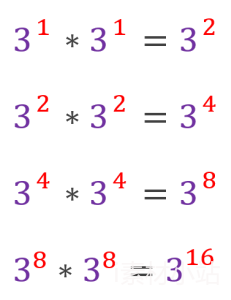
不难得出以下结论
3 ^ n(n为2、4、8、16)都可以由3 ^ 1累乘出来
每一个3 ^ n都有对应的二进制位
3 ^ 1对应二进制位的值是1,实在是二进制10101的最后1位
3 ^ 2对应二进制位的值是0,实在是二进制1010的最后1位
3 ^ 4对应二进制位的值是1,实在是二进制101的最后1位
3 ^ 8对应二进制位的值是0,实在是二进制10的最后1位
3 ^ 16对应二进制位的值是1,实在是二进制1的最后1位
若是3 ^ n对应二进制位的值是0,就不用乘进最终效果
好比3 ^ (8 * 0)、3 ^ (2 * 0)
由于它们最终的值都是3 ^ 0,也就是1
若是3 ^ n对应二进制位的值是1,就需要乘进最终效果
好比3 ^ (16 * 1)、3 ^ (4 * 1)、3 ^ (1 * 1)
以是,综合以上种种结论,可以总结出以下解题步骤
行使3 ^ 1,不停累乘出3 ^ n(n为2、4、8、16)
每当累乘出一个3 ^ n,就查看其对应二进制位的值是1照样0,来决议是否要将它乘进最终效果
int fastPower(int x, int n) {
int result = 1;
while (n != 0) {
if ((n & 1) == 1) {
result *= x;
}
x *= x;
n >>= 1;
}
return result;
}
代入3和21,fastPower(3, 21)的执行流程如下
第1轮while循环
第4行代码
n的二进制是10101(十进制是21)
x = 3 ^ 1, 其对应二进制位的值是1(n的最后一个二进制位)
以是需要执行第5行代码:将x乘进最终效果
result = 3 ^ 1
第7行代码
x = (3 ^ 1) * (3 ^ 1) = 3 ^ 2
第8行代码
n右移1位,其二进制变成了1010(对应的十进制是啥?不重要!!!)
第2轮while循环
第4行代码
n的二进制是1010
x = 3 ^ 2, 其对应二进制位的值是0(n的最后一个二进制位)
以是不需要执行第5行代码:不需要将x乘进最终效果
result = 3 ^ 1
第7行代码
x = (3 ^ 2) * (3 ^ 2) = 3 ^ 4
第8行代码
n右移1位,其二进制变成了101(对应的十进制是啥?不重要!!!)
第3轮while循环
第4行代码
n的二进制是101
x = 3 ^ 4, 其对应二进制位的值是1(n的最后一个二进制位)
以是需要执行第5行代码:将x乘进最终效果
result = (3 ^ 1) * (3 ^ 4)
第7行代码
x = (3 ^ 4) * (3 ^ 4) = (3 ^ 8)
第8行代码
n右移1位,其二进制变成了10(对应的十进制是啥?不重要!!!)
第4轮while循环
第4行代码
n的二进制是10
x = 3 ^ 8, 其对应二进制位的值是0(n的最后一个二进制位)
以是不需要执行第5行代码:不需要将x乘进最终效果
result = (3 ^ 1) * (3 ^ 4)
第7行代码
x = (3 ^ 8) * (3 ^ 8) = 3 ^ 16
第8行代码
n右移1位,其二进制变成了1(对应的十进制是啥?不重要!!!)
第5轮while循环
第4行代码
n的二进制是1
x = 3 ^ 16, 其对应二进制位的值是1(n的最后一个二进制位)
以是需要执行第5行代码:将x乘进最终效果
result = (3 ^ 1) * (3 ^ 4) * (3 ^ 16)
第7行代码
x = (3 ^ 16) * (3 ^ 16) = 3 ^ 32
第8行代码
n右移1位,其二进制变成了0
最后
由于n = 0,以是退出while循环
最终result = (3 ^ 1) * (3 ^ 4) * (3 ^ 16)
复杂度剖析
每执行一次while的循环体,n >>= 1, 会导致n的值减半
以是时间复杂度:O(logn)、空间复杂度:O(1)
Leetcode
Leetcode上的第50号题50. Pow(x, n),恰好就可以用今天解说的快速幂算法。以下是我的代码实现
// 递归
public double myPow(double x, int n) {
if (n == 0) return 1;
if (n == -1) return 1 / x;
double half = myPow(x, n >> 1);
half *= half;
return ((n & 1) == 1) ? half * x : half;
}
// 非递归
public double myPow(double x, int n) {
long y = (n < 0) ? -((long) n) : n;
double result = 1.0;
while (y > 0) {
if ((y & 1) == 1) {
result *= x;
}
x *= x;
y >>= 1;
}
return (n < 0) ? (1 / result) : result;
}
需要提醒的是
这里我用的编程语言是Java,人人可以凭据自己熟悉的编程语言,对一些语法细节作出响应的调整
Leetcode上的n可能是个负数,以是上面的代码针对负数的情形作了一些处置
更多快速幂相关的问题
时间有限,这篇文章就先说到这了哈。给小伙伴们留2个快速幂相关的问题,有空的话,可以去研究一下
使用矩阵快速幂求斐波那契数列
请设计一个算法求x的y次幂模z的效果:(x ^ y) % z
假设x、y都可能是很大的整数(y大于即是0,z不即是0)
若是你稀奇希望我写点什么方面的内容,也可以留言建议,谢谢。迎接关注
原文链接:https://www.cnblogs.com/mjios/p/12690097.html
本站声明:网站内容来源于网络,若有侵权,请联系我们,我们将及时处置。











 - 搜外SEO问答...)

)





