梯度下降和EM算法，kmeans的em推导

I. 牛顿迭代法
给定一个复杂的非线性函数f(x)，希望求它的最小值，我们一般可以这样做，假定它足够光滑，那么它的最小值也就是它的极小值点，满足f′(x0)=0，然后可以转化为求方程f′(x)=0的根了。非线性方程的根我们有个牛顿法，所以

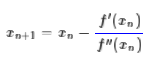
然而，这种做法脱离了几何意义，不能让我们窥探到更多的秘密。我们宁可使用如下的思路：在y=f(x)的x=xn这一点处，我们可以用一条近似的曲线来逼近原函数，如果近似的曲线容易求最小值，那么我们就可以用这个近似的曲线求得的最小值，来近似代替原来曲线的最小值：

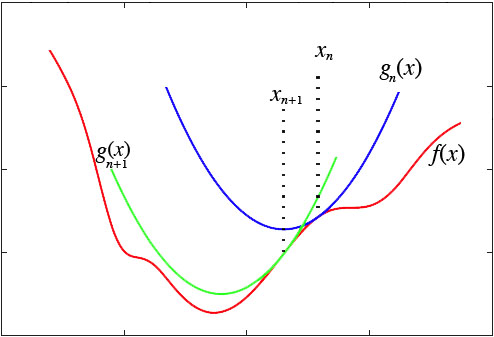
显然，对近似曲线的要求是：
1、跟真实曲线在某种程度上近似，一般而言，要求至少具有一阶的近似度；
2、要有极小值点，并且极小值点容易求解。

这样，我们很自然可以选择“切抛物线”来近似（用二阶泰勒展开近似原曲线）：

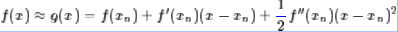
该抛物线具有二阶的精度。对于这条抛物线来说，极值点是(-b/(2*a))

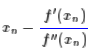
所以我们重新得到了牛顿法的迭代公式：

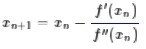
如果f(x)足够光滑并且在全局只有一个极值点，那么牛顿法将会是快速收敛的（速度指数增长），然而真实的函数并没有这么理想，因此，它的缺点就暴露出来了：

1、需要求二阶导数，有些函数求二阶导数之后就相当复杂了；
2、因为f″(xn)的大小不定，所以g(x)开口方向不定，我们无法确定最后得到的结果究竟是极大值还是极小值。

II. 梯度下降

这两个缺点在很多问题上都是致命性的，因此，为了解决这两个问题，我们放弃二阶精度，即去掉f″(xn)，改为一个固定的正数1/h：

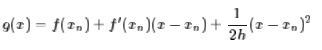
这条近似曲线只有一阶精度，但是同时也去掉了二阶导数的计算，并且保证了这是一条开口向上的抛物线，因此，通过它来迭代，至少可以保证最后会收敛到一个极小值（至少是局部最小值）。上述g(x)的最小值点为

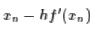
所以我们得到迭代公式

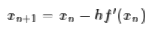
对于高维空间就是

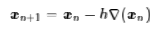
这就是著名的梯度下降法了。当然，它本身存在很多问题，但很多改进的算法都是围绕着它来展开，如随机梯度下降等等。

这里我们将梯度下降法理解为近似抛物线来逼近得到的结果，既然这样子看，读者应该也会想到，凭啥我一定要用抛物线来逼近，用其他曲线来逼近不可以吗？当然可以，对于很多问题来说，梯度下降法还有可能把问题复杂化，也就是说，抛物线失效了，这时候我们就要考虑其他形式的逼近了。事实上，其他逼近方案，基本都被称为EM算法，恰好就只排除掉了系出同源的梯度下降法，实在让人不解。

根据一阶泰勒展开，对于一个可微函数，对于任意的x，有：

$ f(x+\alpha p)=f(x)+\alpha * g(x)*p+o(\alpha *\left| p \right|) $

其中：$ g(x)*p = \left| g(x) \right| *\left| p \right| *cos\theta $ ,$\theta$是两向量之间的夹角,p是搜索方向

当 $\theta $ 为180度得时候，$g(x)*p$ 可取到最小值，即为下降最快的方向。所以，负梯度方向为函数f(x)下降最快的方向，x为未知参数，对X进行迭代更新

如果f(x)是凸函数，则局部最优解就是全局最优解。

V. K-Means

K-Means聚类很容易理解，就是已知N个点的坐标xi,i=1,…,N，然后想办法将这堆点分为K类，每个类有一个聚类中心cj,j=1,…,K，很自然地，一个点所属的类别，就是跟它最近的那个聚类中心cj所代表的类别，这里的距离定义为欧式距离。
所以，K-Means聚类的主要任务就是求聚类中心cj。我们当然希望每个聚类中心正好就在类别的“中心”了，用函数来表示出来，就是希望下述函数L最小(kmeans目标函数是平方损失函数)：

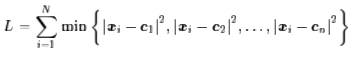
其中，min操作保证了每个点只属于离它最近的那一类。
如果直接用梯度下降法优化L，那么将会遇到很大困难，不过这倒不是因为min操作难以求导，而是因为这是一个NP的问题，理论收敛时间随着N成指数增长。这时我们也是用EM算法的，这时候EM算法表现为：
1、随机选K个点作为初始聚类中心；
2、已知K个聚类中心的前提下，算出各个点分别属于哪一类，然后用同一类的所有点的平均坐标，来作为新的聚类中心。

这种方法迭代几次基本就能够收敛了，那么，这样做的理由又在哪儿呢？

聚类问题：给定数据点 $x_1, x_2, \ldots, x_N \in \mathbb{R}^m$ ，给定分类数目 $K$ ，求出 $K$ 个类中心 $\mu_1, \mu_2, \ldots, \mu_K \in \mathbb{R}^m$ ，使得所有点到距离该点最近的类中心的距离的平方和 $\sum_{i=1}^N{\min_{1\le k \le K} ||x_i-\mu_k||_2^2}$ 最小。

含隐变量的最大似然问题：给定数据点 $x_1, x_2, \ldots, x_N \in \mathbb{R}^m$ ，给定分类数目 $K$ ，考虑如下生成模型，

$p(x,z|\mu_1, \mu_2, \ldots, \mu_K)\propto \begin{cases} \exp\left(-\left|\left|{x-\mu_z}\right|\right|_2^2\right) & ||x-\mu_z||_2=\min_{1\le k \le K} ||x-\mu_k||_2\\ 0 & ||x-\mu_z||_2>\min_{1\le k \le K} ||x-\mu_k||_2 \\ \end{cases}$

模型中 $z\in\{1,2,\ldots,K\}$ 为隐变量，表示簇的类别。

这个式子的直观意义是这样的，对于某个将要生成的点 $x$ 和类别号 $z$ ，如果不满足“ $x$ 到中心 $\mu_z$ 的距离小于等于 $x$ 到其他中心 $\mu_k$ 的距离”的话，则不生成这个点。如果满足的话，则 $z$ 取值就是这个“最近的”类中心的编号（如果有多个则均等概率随机取一个），以高斯的概率密度在这个类中心周围生成点 $x$ 。

用EM算法解这个含隐变量的最大似然问题就等价于用K-means算法解原聚类问题。

Q函数是完全数据的对数似然函数关于在给定X和参数$\mu$的情况下对隐变量Z的条件概率的期望，em算法通过求解对数似然函数的下界的极大值逼近求解对数似然函数的极大值。

这和K-means算法中根据当前分配的样本点求新的聚类中心的操作是一样的。

k-means是GMM的简化，而不是特例。

共同点：都是使用交替优化算法，要优化的参数分为两组，固定一组，优化另一组。

GMM是先固定模型参数，优化 $\gamma(z_{nk})$ ；然后固定 $\gamma(z_{nk})$ ，优化 $\mu, \Sigma, \pi$ 。
k-means是先固定 $\mu$ (聚类中心)，优化聚类赋值；然后固定聚类赋值，优化 $\mu$ 。

k-means对GMM的简化有：

$\pi_k = 1/K$ ，模型中混合权重相等
$\Sigma_k = \epsilon I$ ，各个成分的协方差相等，且固定为单位矩阵的倍数
$x_n$ 分配给各个component的方式，由基于概率变为winner-take-all方式的 hard 赋值。（kmeans中，某样本点和模型中某个子成分，如果该样本点与子成分的中心距离最小，则以高斯的概率密度在中心点周围生成这个点，否则就不生成这个点。而GMM中，每个子成分都有可能生成该样本点，概率值为子成分的系数）