微分几何和微分流形的书上经常提到“正则曲线”和“正则曲面”。其实英文书中写作”Regular Curve“和”Regular Surface“，让人一眼能够了解其大意（这也是我更偏向看英文原版书的原因）。我就想，数学家为啥不翻译成”规则曲线“和”规则曲面“呢？难道是为了更进一步提高数学的门槛？

言归正传，我们来看看Regular Curve和Regular Surface的真正的数学含义。（参考Manfredo P. do Carmo的《Differential Geometry of Curves and Surfaces》）

1. Regular Curve

我们学习微积分的时候，已经知道了”连续“以及”可微“的概念（所谓可微就是函数连续的前提下，左导数等于右导数）。在微分几何中一条参数化可微曲线可以作如下定义：

一条参数化的可微曲线是定义在一个开区间上的可微映射：

举例1：直线，

举例2：圆，

举例3：

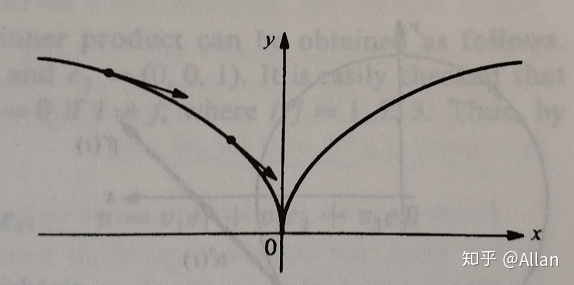
举例4：折线

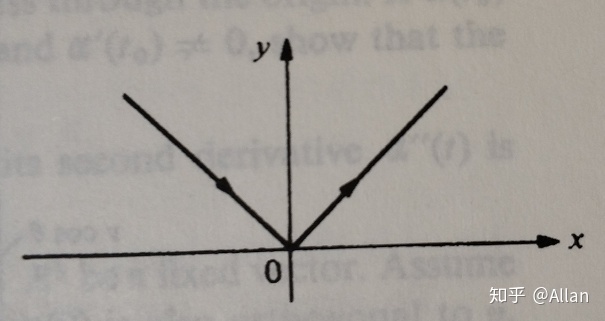
举例5：自相交曲线

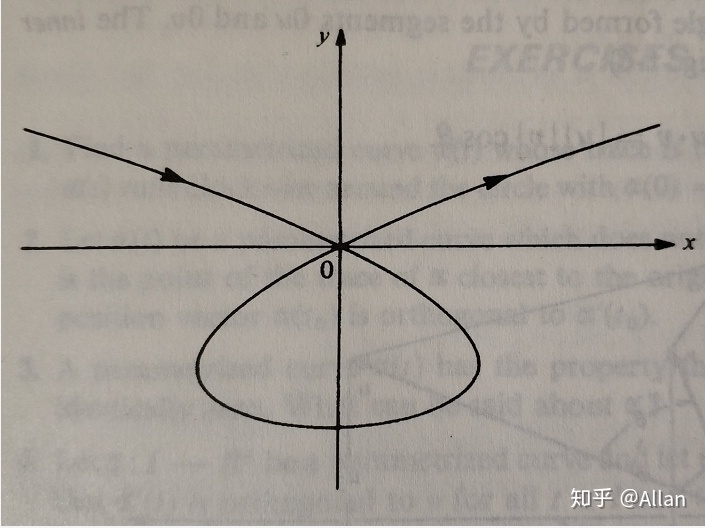
总结一下正则曲线（Regular Curve）的定义：

一条参数化的可微曲线

也就是说：正则曲线在满足连续可微条件之外，必须保证每一处的切向量不为0。

2. Regular Surface

对于曲面，首先我们知道曲面是一个二维到三维的映射，用数学的语言描述一下就是

那么我们如何定义一个正则曲面呢？

我们可以这样想：过曲面上一点P有无数条在此曲面上的曲线，这些曲线在P的邻域内都是正则曲线（连续可微有非0切向量），并且在这些曲线在P的邻域内不会自相交（记住正则曲线不能保证曲线不会自相交哦），那么这个P点就是曲面上的正则点，如果曲面上所有的点都是正则点，那么这个曲面就是正则曲面！

下面我们用数学的语言来描述一下正则曲面：

1）曲面的映射

其中

2） 曲面的映射

https://zh.wikipedia.org/wiki/%E5%90%8C%E8%83%9A， 同胚指的是满足单射、满射、连续并且逆连续）。同胚保证了U和V之间元素的一对一关系，避免了自相交。

3）对于任意的

关于

Allan："dF" 的本质 （雅可比矩阵）​zhuanlan.zhihu.com

这里的一对一映射指的是，对于

第1）条的作用是保证了曲面没有尖点，没有尖边，第2）条的作用是保证了曲面没有自相交，第3）条的作用比较none-trival，它的作用是保证曲面上的每点都有切平面，下面详细解释一下。

我们知道