1、信息增益（互信息）介绍

由于在最终的bayse算法中只使用了部分的特征，而特征的选择使用到了信息增益，所以在这里做一个简单的介绍。

（1）西瓜书中的信息增益¹

在西瓜书的4.2节中，选择树节点的划分属性时提到了信息增益；其定义如下：
首先是元集合D的类别信息熵

$$Ent(D)=-\sum _{k=1}^{|y|}{p}_{k}lo{g}_2(p_k)$$
然后根据属性a划分为了V个集合后，给出了信息增益的定义：
$$Gain(D,a)=Ent(D)-\sum _{v=1}^V\frac{\left|D^v\right|}{\left|D\right|}Ent(D^v)$$
然后利用信息增益来进行树的划分特征的选取。

（2）PRML中的互信息²

在PRML1.6.1中定义了互信息，公式如下：
$$I[x,y]\equiv KL(p(x,y)||p(x)p(y))=-\iint p(x,y)ln(\frac{p(x)p(y)}{p(x,y)})dxdy$$
化简后可以得到：
$$I[x,y]\equiv H[x]-H[x|y]=H[y]-H[y|x]$$

（3） 其实他们是一个东西

证明：首先把1、->（2）中的积分形式改写成和的形式，并把ln还成log（相差了log2倍），有
$$-\sum _{x,y}p(x,y)lo{g}_2(\frac{p(x)p(y)}{p(x,y)})$$
$$=-\sum _y\sum _{x}p(x,y)lo{g}_2(p(y))-(-\sum _{x}p(x)\sum _{y}p(y|x)lo{g}_2(p(y|x)))$$
$$=-\sum _{y}p(y)lo{g}_2(p(y))-(-\sum _{x}p(x)\sum _{y}p(y|x)lo{g}_2(p(y|x)))$$

仔细观察·是不是和1、->(1)一模一样！如下图所示：

2、朴素Bayse新闻分类³

（1）常量及辅助函数

import math
import random
import collections
label_dict = {0: '财经', 1: '健康', 2: '教育', 3: '军事', 4: '科技',5: '旅游', 6: '母婴', 7: '汽车', 8: '体育',9: '文化', 10: '娱乐'}def code_2_label(code):return label_dict.get(code)def default_doc_dict():"""构造和类别数等长的0向量:return: 一个长度和文档类别数相同的全0数组，用来作为某些以该长度数组为值的字典的默认返回值"""return [0] * len(label_dict)def shuffle(in_file):"""简单的乱序操作，用于生成训练集和测试集:param in_file: 输入文件:return:"""text_lines = [line.strip() for line in open(in_file, encoding='utf-8')]print('正在准备训练数据和测试数据，请稍后...')random.shuffle(text_lines)total_lines = len(text_lines)train_text = text_lines[:int(3 * total_lines / 5)]test_text = text_lines[int(3 * total_lines / 5):]print('准备训练数据和测试数据完毕，下一步...')return train_text, test_text

（2）特征提取

根据1中的信息增益（互信息）的大小来提取前100个最重要的特征(这里就是词了)
首先定义了如下的计算互信息的辅助函数，它所计算的内容其实是：

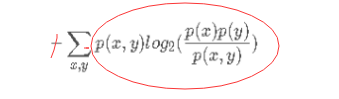
（注意红色的-，我把它移到了和的内部）

def mutual_info(N, Nij, N_i, N_j):"""计算互信息，这里log的底取为2;同时为了防止Nij为0，分子做了+1的平滑:param N:总样本数:param Nij:x为i，y为j的样本数:param N_i:x为i的样本数:param N_j:y为j的样本数:return:"""return Nij * 1.0 / N * math.log(N * (Nij + 1) * 1.0 / (N_i * N_j)) / math.log(2)

看起来并不是很清晰，因为是化简以后的。这里进行一下推导：
$$-p(x=i,y=j)lo{g}_2(\frac{p(x=i)p(y=j)}{p(x=i,y=j)})$$
$$=-\frac{N_{i,j}}{N}\ast lo{g}_2(\frac{\frac{N_i}{N}\frac{N_j}{N}}{\frac{N_{i,j}}{N}})$$
$$=\frac{N_{i,j}}{N}\ast lo{g}_2(\frac{N{N}_{i,j}}{N_i{N}_j})$$
$$=\frac{N_{i,j}}{N}\ast ln(\frac{N{N}_{i,j}}{N_i{N}_j})/ln(2)$$
加上平滑以后，就得到了上面的函数（别在乎1.0，只是整数转浮点数）
$$=\frac{N_{i,j}}{N}\ast ln(\frac{N(N_{i,j}+1)}{N_i{N}_j})/ln(2)$$

def count_for_cates(train_text, feature_file):"""遍历文件，统计每个词在每个类别中出现的次数，以及每个类别中的文档数，并将结果写入特征文件(只写互信息值最大的前100项):param train_text::param feature_file::return:"""# 各个类别中所包含的词的个数doc_count = [0] * len(label_dict)# 以word为key的字典，value是对应该word# 在每个类别中出现次数的向量;该词不存在就返回全0的向量word_count = collections.defaultdict(default_doc_dict)# 扫描文件和计数for line in train_text:label, text = line.strip().rstrip('\n').split(' ', 1)words = text.split(' ')int_label = int(label)for word in words:# 空字符串用了停用词也没有过滤掉，就在这里处理了if word != '':word_count[word][int_label] += 1doc_count[int_label] += 1# 计算互信息print('计算互信息，提取关键/特征词中，请稍后...')# 互信息结果字典，value描述的是某个类别中的词数# 衡量的信息量与明确是某个词以后的以词数衡量的信息量的互信息mi_dict = collections.defaultdict(default_doc_dict)# 词总量N = sum(doc_count)# (word,[...各个类别中该词出现的词数...])for k, vs in word_count.items():for i in range(len(vs)):# N11代表是词k并且出现在类别i中的词数N11 = vs[i]# N10 代表是词k但未出现在类别i中的词数N10 = sum(vs) - N11# N01 代表不是词k但出现在类别i中的词数N01 = doc_count[i] - N11# N00 代表不是词k也未出现在类别i中的词数N00 = N - N11 - N10 - N01"""设D为某个类别中的词总数，A为某个词出现的总次数，N为总词数则下面的式子表达的是mutual_info(N,DA,A,D) + mutual_info(N,~DA, A, ~D) + mutual_info(N,D~A, D, ~A) + mutual_info(N, ~D~A, ~D, ~A)"""mi = mutual_info(N, N11, N10 + N11, N01 + N11) + mutual_info(N, N10, N10 + N11, N00 + N10) + mutual_info(N, N01, N01 + N11, N01 + N00) + mutual_info(N, N00, N00 + N10, N00 + N01)mi_dict[k][i] = mi# 用来作为bayes参数的词f_words = set()# 把每类文档分类最重要的100个词放到f_words中for i in range(len(doc_count)):sorted_dict = sorted(mi_dict.items(), key=lambda x: x[1][i], reverse=True)for j in range(100):f_words.add(sorted_dict[j][0])with open(feature_file, 'w', encoding='utf-8') as out:# 输出每个类别中包含的词的数量out.write(str(doc_count) + '\n')# 输出作为参数的词for f_word in f_words:out.write(f_word + "\n")print("特征词写入完毕...")

def load_feature_words(feature_file):"""从特征文件中导入特征词:param feature_file::return:"""with open(feature_file, encoding='utf-8') as f:# 每个类别中包含的词的数量doc_words_count = eval(f.readline())features = set()# 读取特征词for line in f:features.add(line.strip())return doc_words_count, features

（3）训练模型

def train_bayes(feature_file, text, model_file):"""训练贝叶斯模型，实际上计算每个类别中特征词的出现次数:param feature_file: 特征文件:param text: 原始的样本:param model_file: 模型文件:return:"""print('使用朴素贝叶斯训练中...')doc_words_count, features = load_feature_words(feature_file)feature_word_count = collections.defaultdict(default_doc_dict)# 每类文档中特征词出现的总次数feature_doc_words_count = [0] * len(doc_words_count)for line in text:label, text = line.strip().rstrip('\n').split(' ', 1)int_label = int(label)words = text.split(' ')for word in words:if word in features:feature_doc_words_count[int_label] += 1feature_word_count[word][int_label] += 1out_model = open(model_file, 'w', encoding='utf-8')print('训练完毕，写入模型...')for k, v in feature_word_count.items():scores = [(v[i] + 1) * 1.0 / (feature_doc_words_count[i] + len(feature_word_count)) for i in range(len(v))]out_model.write(k + '\t' + str(scores) + '\n')

def load_model(model_file):"""从模型文件中导入计算好的贝叶斯模型:param model_file::return:"""print('加载模型中...')with open(model_file, encoding='utf-8') as f:scores = {}for line in f.readlines():word, counts = line.split('\t', 1)scores[word] = eval(counts)return scores

（4）预测

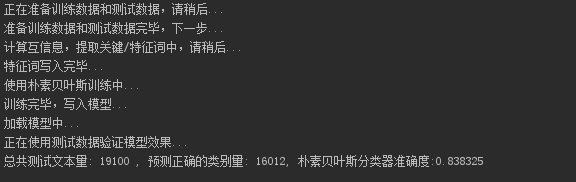
def predict(feature_file, model_file, test_text):"""预测文档的类别，标准输入每一行为一个文档这是一个朴素贝叶斯的预测方法p(c|x) 正比于 p(c)p(x1|c)....p(xn|c):param feature_file::param model_file::param test_text::return:"""doc_words_count, features = load_feature_words(feature_file)# p(c)doc_scores = [math.log(count * 1.0 / sum(doc_words_count)) for count in doc_words_count]scores = load_model(model_file)r_count = 0doc_count = 0print("正在使用测试数据验证模型效果...")for line in test_text:label, text = line.strip().split(' ', 1)int_label = int(label)words = text.split(' ')pre_values = list(doc_scores)for word in words:if word in features:for i in range(len(pre_values)):pre_values[i] += math.log(scores[word][i])m = max(pre_values)p_index = pre_values.index(m)if p_index == int_label:r_count += 1doc_count += 1print("总共测试文本量: %d ,预测正确的类别量:%d,朴素贝叶斯分类器准确度:%f" %(doc_count, r_count, r_count * 1.0 / doc_count))

（5）测试

if __name__ == '__main__':out_in_file = 'd:/nlps/result.txt'out_feature_file = 'd:/nlps/feature.txt'out_model_file = 'd:/nlps/model.txt'train_text, test_text = shuffle(out_in_file)count_for_cates(train_text, out_feature_file)train_bayes(out_feature_file, train_text, out_model_file)predict(out_feature_file, out_model_file, test_text)

（6）测试结果

---

1. 周志华 《机器学习》 4.2节 ↩︎

2. Bishop “Pattern Recognition and Machine Learning” 1.6.1 ↩︎

3. 寒小阳 ↩︎