白盒测试逻辑覆盖（语句覆盖、判定覆盖、条件覆盖、判定/条件覆盖、条件组合覆盖）
逻辑覆盖测试：
- 语句覆盖：每条语句至少执行一次
- 判定覆盖：每一判定的每个分支至少执行一次
- 条件覆盖：每一判定中的每个条件，分别按真、假至少各执行一次
- 判定/条件覆盖：同时满足判定覆盖和条件覆盖的要求
- 条件组合覆盖：求出判定中所有条件的各种可能组合值，每一可能的条件组合至少执行一次
注： 上述逻辑覆盖测试的5种标准从上至下发现错误的能力由弱变强
表1 逻辑覆盖测试的5种标准
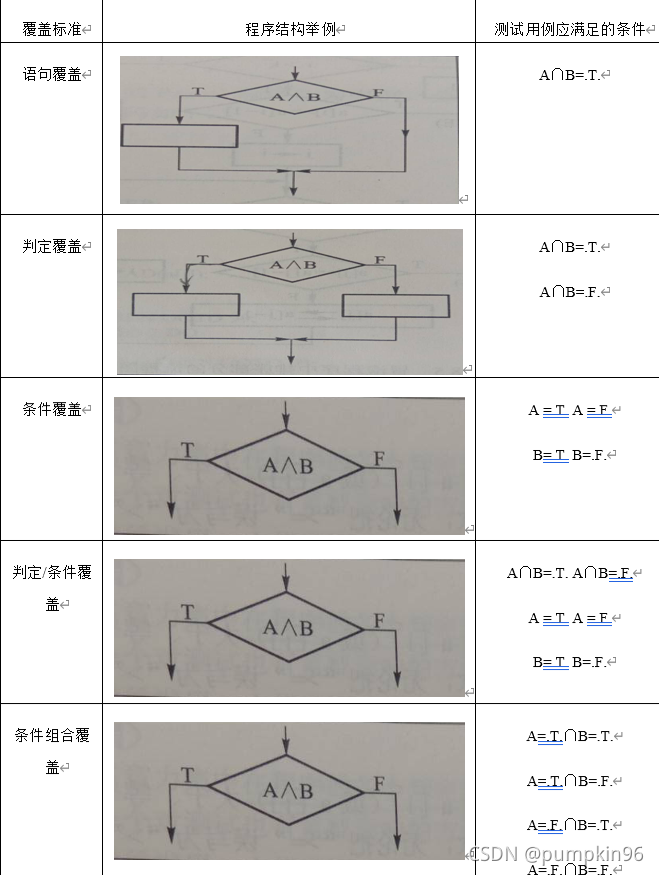
接下来详细介绍每一种覆盖的条件
一、语句覆盖：
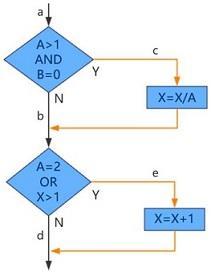
只需要遍历路径ace，便将程序中的所有语句便都执行了一次。生成的用例及其遍历路径如下：
A=2，B=0，X=4 ace
缺点：语句覆盖是“最弱的覆盖”，它难以发现程序中的错误。①程序中存在一条x的值未发生改变的路径abd没有测试。②它无法发现判定的错误，比如第一个判定条件也许应该是“或”，而不是“与”。③无法发现条件的错误，比如第二个判断中的条件X>1，也许事实上应该是X>0。
二、判定覆盖
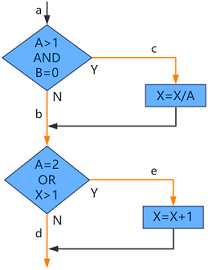
只需要涵盖路径ace和abd，或涵盖路径acd和abe，就可以使得两个判定为“真”和为“假”的分支都执行一次。如果选择后一种情况，生成的用例及其遍历的路径如下：
A=3，B=0，X=3 acd
A=2，B=1，X=1 abe
我们仅有50%的可能性遍历到X值未发生改变的路径，即，只有我们选择涵盖路径ace和abd的情况，而不是涵盖路径acd和abe时。对应的测试用例如下：
A=2，B=0，X=2 ace
A=3，B=1，X=1 abd
缺点：这两组测试用例都存在同一个问题：当判定由多个条件组合构成时，它未必能发现每个条件的错误。如果第二个判定把条件X>1错误的写成了X<1，我们设计的测试用例仍然无法找出这个错误。
三、条件覆盖
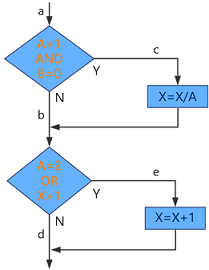
第一个判断的所有条件的可能取值情况是A>1或A≤1，B=0或B≠0。第二个判断的所有条件可能的取值情况为A=2或A≠2，X>1或X≤1。生成的用例及其遍历的路径如下所示：
A=1，B=0，X=3 abe
A=2，B=1，X=1 abe
缺点：条件覆盖并不一定总能覆盖全部分支。测试用例虽然满足了条件覆盖准则，但是只涵盖了程序的路径abe。但是，条件覆盖还是要比判定覆盖强一些，因为条件覆盖可能会使判断中各个条件的结果都取“真”或着取“假”，而判定覆盖却做不到这一点。
四、判定/条件覆盖
判定/条件覆盖
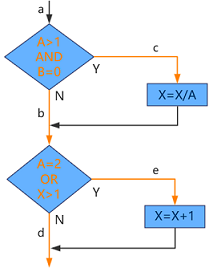
判定/条件覆盖，既要考虑到单个判定中每个条件的可能情况（A>1或A≤1，B=0或B≠0，A=2或A≠2，X>1或X≤1），也要考虑到每个判定的可能情况（路径ace和abd，或路径acd和abe）。用例及其遍历的路径如下所示：
A=2，B=0，X=4 ace
A=1，B=1，X=1 abd
缺点：条件覆盖和判定/条件覆盖不一定会发现逻辑表达式中的错误。尽管看上去所有条件的所有结果似乎都执行到了，但由于有些条件会屏蔽掉后面的条件，并不一定能全部执行得到。例如，上述测试用例①满足了条件A=2后，就不再执行对条件X>1的判断；测试用例②中不满足条件A>1后，就不再执行对条件B=0的判断。
五、条件组合覆盖
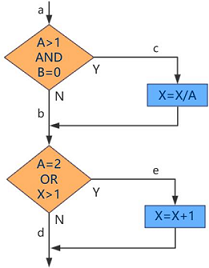
满足多重条件覆盖准则的测试用例，必须覆盖以下8种组合：
第一个判定的取值情况 第二个判定的取值情况
- A>1，B=0 5. A=2，X>1
- A>1，B≠0 6. A=2，X≤1
- A≤1，B=0 7. A≠2，X>1
- A≤1，B≠0 8. A≠2，X≤1
生成的测试用例，以及它们遍历的路径和覆盖的组合如下：
A=2，B=0，X=4 ace 覆盖组合1，5
A=2，B=1，X=1 abe 覆盖组合2，6
A=1，B=0，X=2 abe 覆盖组合3，7
A=1，B=1，X=1 abd 覆盖组合4，8
缺点：多重条件覆盖不一定能覆盖到每条路径，路径acd就被遗漏掉了。
