本文使用 Zhihu On VSCode 创作并发布

前面写的一些统计学习方法都是属于监督学习（supervised learning），这篇主成分分析（principal components analysis，简称 PCA ）和下一篇聚类分析（clustering）都是属于非监督学习（unsupervised learning）。

之前 ISLR读书笔记十二 中已经提到过主成分这一概念。其主要目的是利用一小部分数据组合，尽可能多地体现 全部数据的特征，从而实现降维的作用。

这里的 尽可能多地体现 可以有两种解读：

1. 将数据投影到方差最大的方向上，尽可能保留方差信息

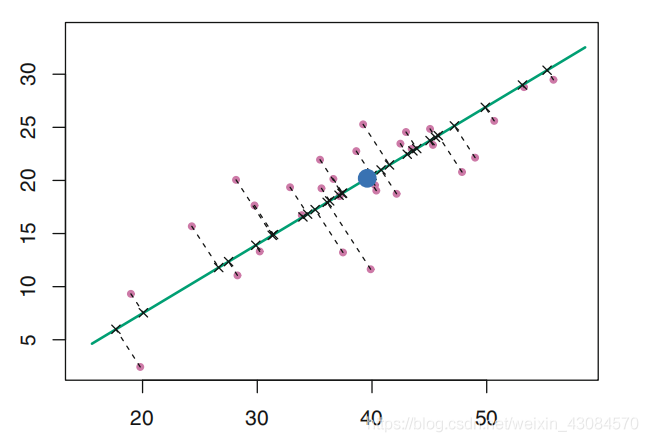
2. 低维空间下的最佳近似。

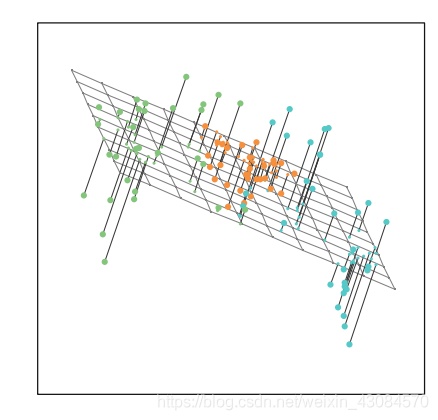
从第一种解读出发，计算第一主成分：
令

这里要求

，

称作加载（loadings），

称作加载向量（loading vector）

第一主成分使得样本方差最大。即

由于

，所以即，使得

最大。这里，

称作分数（scores）

该优化问题，可以用奇异值分解（SVD）的方法解得。

第二主成分是所有与第一主成分

不相关（uncorrelated）的，关于

的线性组合中，方差最大的线性组合。令

可以证明

与

不相关，等价于加载向量

与

正交。

第三主成分是所有与

、

不相关（uncorrelated）的，关于

的线性组合中，方差最大的线性组合。以此类推。

从第二种解读出发，第一主成分加载向量是

维空间中，最接近

个观测数据的直线（在欧式距离平方的均值下最接近）。

个主成分的分数向量和加载向量，构成了原始

维数据在

维空间的最佳近似，即

另外 PCA 还有其他一些需要注意的点：

规模化：

数据通常需要提前进行规模化（scaled）（每个变量乘以不同的常数），使得每个自变量的标准差为1。否则如果有部分变量方差特别大，那么PCA 的结果会受很大影响。

唯一性

每一个主成分在相差一个正负号的意义下式唯一的

被解释方差比例

我们通常关心前几个主成分反映了多少方差
数据总方差定义如下

第

个主成分的被解释方差定义如下：

第

个主成分被解释方差的比例（proportion of variance explained）

决定主成分的个数

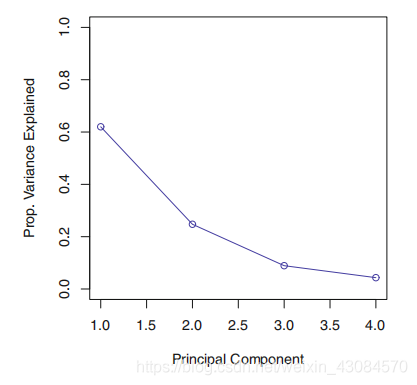
可以通过碎石图（scree plot），来决定主成分的个数
方法是寻找一个点，在这个点之后的点，主成分被解释方差比例很小