方案设计问题在一元一次方程实际问题中有所接触，在一次函数实际应用题中也有。一次函数中的方案设计问题，常与一次函数的性质、不等式(组)、方程组等知识点相结合，这类题目一旦掌握解题方法，难度不是很大。本篇文章主要介绍一次函数方案设计的两类问题，解题思路不一样。

这两类问题都是运输问题，一类需要借助表格法解题，还有一类是直接找等量关系式进行解题。

类型一：等量关系式

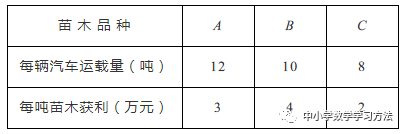
例题1：我区花木城组织10辆汽车装运完A、B、C三种不同品质的苗木共100吨到外地销售，按计划10辆汽车都要装满，且每辆汽车只能装同一种苗木，由信息解答以下问题：

(1)设装A种苗木车辆数为x，装运B种苗木的车辆数为y，求y与x之间的函数关系式；

(2)若装运每种苗木的车辆都不少于2辆，则车辆安排方案有几种？写出每种安排方案；

(3)若要使此次销售获利最大，应采用哪种安排方案？并求出最大利润的值．

分析：本题设置了三小问，由易到难，基本上将解题思路交代的比较清楚。第一小问借助10辆车、100吨两个数据，可以得到等量关系。已知装A种苗木的车辆数为x，装B种苗木的车辆数为y辆，一共有10辆车，那么装C种苗木的车辆数为10-x-y。再根据一共有100吨，得到关于x、y的等式，化简即可。

解：(1)由装A种为x辆，装B种为y辆，装C种为(10-x-y)辆，

由题意得：12x+10y+8(10-x-y)=100∴y=10-2x．

根据“若装运每种苗木的车辆都不少于2辆”，那么可以得到不等式组，即装A、B、C三种苗木的车辆数都要为非负数。

(2)∵10-x-y=10-x-(10-2x)=x，故装C种车也为 x 辆．

由x≥2；y≥2；10xy≥2，解得：2≤x≤4，

∵x应取整数，

∴x=2或x=3或x=4，

∴车辆的安排方案有三种．

方案一：安排2辆汽车运A品种，6辆汽车运B品种，2辆汽车运C品种；

方案二：安排3辆汽车运A品种，4辆汽车运B品种，3辆汽车运C品种；

方案三：安排4辆汽车运A品种，2辆汽车运B品种，4辆汽车运C品种．

设最大利润为W(万元)，分别表示出运输A、B、C的利润，然后相加，得到W关于x的一次函数，通过一次函数的增减性得到利润的最大值。

(3)设销售利润为W(万元)，

则W=3×12x+4×10×(10-2x)+2×8x=-28x+400，

∵k=-28＜0，

∴W随x的减小而增大，

∴当x=2时，W取最大值，W最大值=344．

即应采用方案一可获得最大利润，最大利润为344万元．

类型二：列表法

例题2：某公司在A、B两地分别有某种库存物资20和30吨，需要将这些物资运往C、D两地，其中C地需要28吨，D地需要22吨，从A地运往从C、D两地的费用分别为每吨100元和150元，从B地运往从C、D两地的费用分别为每吨80元和每吨120元，公司应设计怎样的调运方案使这些物资的总运费最省．

分析：本题涉及有A、B两地，C、D两地，库存物资，所需物资这些量，我们可以设计一张表格，将这些量全部体现在表格上，设从A地运往C地x吨，列表如下：

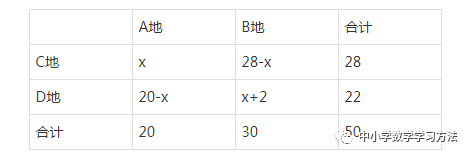
通过这张表格，我们可以得到如下信息：A地运往C地x吨，A第运往D地(20-x)吨，B地运往C地(28-x)吨，B地运往D地(x+2)吨；再结合上述的费用，可以得到A地运往C地的费用为100x，A第运往D地的费用为150(20-x)，B地运往C地的费用为80(28-x)，B地运往D地的费用为120(x+2)，由此可以得到总费用。

当然，我们也可以将费用在表格中同时体现出来，这样会更加清楚。除此之外，通过这张表格，我们还可以得到关于自变量的取值范围，因为表格中的四个数据都是非负数，由此得到关于x的不等式组，通过解不等式组得到自变量的取值范围。

解：设从A地运往C地x吨，则运往D地(20-x)吨，从B地运往C地(28-x)吨，运往D地22-(20-x)=(x+2)吨，总费用为w元，

根据题意可得，w=100x+150(20-x)+80(28-x)+120(x+2)=-10x+5480，

∵k=-10＜0

∴w随x的增大而减小，

∴当x=20时，w取得最小值，此时20-x=0，28-x=8，x+2=22，

即从A地运往C地20吨，运往D地0吨，从B地运往C地8吨，运往D地22吨，总费用最省．