Python小白的数学建模课-16.最短路径算法

最短路径问题是图论研究中的经典算法问题，用于计算图中一个顶点到另一个顶点的最短路径。
在图论中，最短路径长度与最短路径距离却是不同的概念和问题，经常会被混淆。
求最短路径长度的常用算法是 Dijkstra 算法、Bellman-Ford 算法和Floyd 算法，另外还有启发式算法 A*。
『Python小白的数学建模课 @ Youcans』带你从数模小白成为国赛达人。

1. 最短路径问题

最短路径问题是图论研究中的经典算法问题，用于计算图中一个顶点到另一个顶点的最短路径。

最短路径问题有几种形式：确定起点的最短路径，确定终点的最短路径，确定起点和终点的最短路径，全局最短路径问题。

1.1 最短路径长度与最短路径距离

在日常生活中，最短路径长度与最短路径距离好像并没什么区别。但在图论中最短路径长度与最短路径距离却是不同的概念和问题，经常会被混淆。

图论中有无权图和有权图，无权图中的边没有权，赋权图的边带有权，可以表示距离、时间、费用或其它指标。在问题文字描述中，往往并不直接指出是无权图还是有权图，这时就要特别注意最短路径与最短加权路径的区别。

路径长度是把每个顶点到相邻顶点的长度记为 1，而不是指这两个顶点之间道路的距离——两个顶点之间的道路距离是连接边的权（weight）。

通俗地说，路径长度可以认为是飞行棋的步数，或者公交站点的站数，相邻顶点之间为一步，相隔几个顶点就是几站。路径长度是从路径起点到终点的步数，计算最短路径是要计算从起点到终点步数最少的路径。

如果问题不涉及相邻顶点间的距离，要计算从起点到终点的最短路径及对应的最短路径长度，是指这条路径从起点到终点有几步（站），在图论中称为最短路径长度。但是，如果问题给出相邻顶点之间的道路长度或距离，姑且称为各路段的距离，要计算从起点到终点的最短路径及对应的最短距离，显然并不是要找经过最少步数的路径，而是在找路径中各路段的距离之和最小的路径，在图论中称为最短加权路径长度——这里权重是路段距离。

相邻顶点的连接边的权，不仅可以是路段距离，也可以是时间、费用等指标。问题就变成寻求最短时间、最低成本的路径，这实际上也是最短加权路径长度问题。

1.2 最短路径的常用算法

求解最短路径长度的常用算法是 Dijkstra 算法、Bellman-Ford 算法和Floyd 算法，另外还有启发式算法 A*。

1.2.1 Dijkstra 算法

Dijkstra 算法是经典的最短路径算法，在数据结构、图论、运筹学中都是教学的基本算法。有趣的是，在数据结构中 Dijkstra 算法通常是按贪心法讲述，而在运筹学中则被认为是动态规划法。

Dijkstra算法从起点开始，采用贪心法策略，每次遍历距离起点最近且未访问过的邻接顶点，层层扩展直到终点为止。

Dijkstra算法可以求出加权最短路径的最优解，算法的时间复杂度为 O(n^2)。如果边数远小于 n^2，可以用堆结构将复杂度降为O((m+n)log(n))。

Dijkstar算法不能处理负权边，这是由于贪心法的选择规则决定的。

1.2.2 Bellman-Ford 算法

Bellman-Ford 算法是求含负权图的单源最短路径算法。算法原理是对图进行 V-1次松弛操作，得到所有可能的最短路径。

Bellman-Ford 算法可以处理负权边。其基本操作“拓展”是在深度上搜索，而“松弛”操作则在广度上搜索，因此可以对负权边进行操作而不影响结果。

Bellman-Ford 算法的效率很低，时间复杂度高达 O(V*E)，V、E 分别是顶点和边的数量。SPFA 是 Bellman-Ford 的队列优化，通过维护一个队列极大地减少了重复计算，时间复杂度为 O(k*E) 。

Dijkstra 算法在求解过程中，起点到各顶点的最短路径求出后就不变了。Bellman算法在求解过程中，每次循环都要修改所有顶点间的距离，起点到各顶点最短路径一直要到算法结束才确定。

1.2.3 Floyd 算法

Floyd 算法又称插点法，运用动态规划思想求解有权图中多源点之间最短路径问题。算法从图的带权邻接矩阵开始，递归地进行 n 次更新得到图的距离矩阵，进而可以得到最短路径节点矩阵。

Floyd 算法的时间复杂度为 O(n^3)，空间复杂度为 O(n^2)。算法时间复杂度较高，不适合计算大量数据。Floyd 算法的优点是可以一次性求解任意两个节点之间的最短距离，对于稠密图的效率高于执行 V 次 Dijkstra算法。

Floyd 算法可以处理负权边。

Floyd 算法号称只有 5行代码，我们来欣赏一下：

for(k=0;k<n;k++)//中转站0~kfor(i=0;i<n;i++) //i为起点for(j=0;j<n;j++) //j为终点if(d[i][j]>d[i][k]+d[k][j])//松弛操作 d[i][j]=d[i][k]+d[k][j];

1.2.4 A* 算法

A*算法是一种静态路网中求解最短路径最有效的直接搜索方法。

A*算法是启发式算法，采用最佳优先（Best-first）搜索策略，基于估价函数对每个搜索位置的评估结果，猜测最好的位置优先进行搜索。

A*算法极大地减少了低质量的搜索路径，因而搜索效率很高，比传统的路径规划算法实时性更高、灵活性更强；但是，A*算法找到的是相对最优路径，不是绝对的最短路径，适合大规模、实时性高的问题。

1.3 最短路径算法的选择

需要求解任意两个节点之间的最短距离，使用 Floyd 算法；
只要求解单源最短路径问题，有负权边时使用 Bellman-Ford 算法，没有负权边时使用 Dijkstra 算法；
A*算法找到的是相对最优路径，适合大规模、实时性高的问题。

2. NetworkX 中的最短路径算法

NetworkX 提供了丰富的最短路径函数，除了常见的 Dijkstra 算法、Bellman-ford 算法、Floyd Warshall 算法和 A*算法，还有 Goldbery-Radzik 算法和 Johnson 算法。其中，Bellman-ford 算法函数使用的是队列改进算法，即以 SPFA 算法实现。

2.1 无向图和有向图的最短路径求解函数

函数	功能
shortest_path(G[, source, target, weight,…])	计算图中的最短路径
all_shortest_paths(G, source, target[,…])	计算图中所有最短的简单路径
shortest_path_length(G[, source, target, …])	计算图中的最短路径长度
average_shortest_path_length(G[, weight, method])	计算平均最短路径长度

其中，最基本的求解最短路径函数 shortest() 和最短路径长度 shortest_path_length() 是 ‘dijkstra’ 算法和 ‘bellman-ford’ 算法的集成接口，可以通过 method=‘dijkstra’ 选择不同的算法。

shortest_path(G, source=None, target=None, weight=None, method=‘dijkstra’)
shortest_path_length(G, source=None, target=None, weight=None, method=‘dijkstra’)

主要参数：

G(NetworkX graph)：图。
source (node)：起点。
target (node)：终点。
weight (string or function)：参数为字符串(string)时，按该字符串查找边的属性作为权重；如果该字符串对应的边属性不存在，则权重置为 1；参数为函数时，边的权重是函数的返回值。
method [string, optional (default = ‘dijkstra’)]：支持的选项为 ‘dijkstra’, ‘bellman-ford’。

2.2 无权图最短路径算法

函数	功能
single_source_shortest_path(G, source[,cutoff])	计算从源到所有可达节点的最短路径
single_source_shortest_path_length(G,source)	计算从源到所有可达节点的最短路径长度
single_target_shortest_path(G, target[,cutoff])	计算从所有可达节点到目标的最短路径
single_target_shortest_path_length(G,target)	计算从所有可达节点到目标的最短路径长度
all_pairs_shortest_path(G[, cutoff])	计算所有节点之间的最短路径
all_pairs_shortest_path_length(G[, cutoff])	计算所有节点之间的最短路径长度

2.3 有权图最短路径算法

函数	功能
dijkstra_path(G, source, target[, weight])	计算从源到目标的最短加权路径
dijkstra_path_length(G, source, target[,weight])	计算从源到目标的最短加权路径长度
all_pairs_dijkstra_path(G[, cutoff, weight])	计算所有节点之间的最短加权路径
all_pairs_dijkstra_path_length(G[, cutoff,… ])	计算所有节点之间的最短加权路径长度
bellman_ford_path(G, source, target[, weight])	计算从源到目标的最短路径
bellman_ford_path_length(G, source, target)	计算从源到目标的最短路径长度
all_pairs_bellman_ford_path(G[, weight])	计算所有节点之间的最短路径
all_pairs_bellman_ford_path_length(G[,weight])	计算所有节点之间的最短路径长度
floyd_warshall(G[, weight])	用 Floyd 法计算所有节点之间的最短路径长度
floyd_warshall_numpy(G[, nodelist, weight])	用 Floyd 法计算所有指定节点之间的最短路径长度

3. NetworkX 中的 Dijkstra 算法

NetworkX 中关于 Dijkstra 算法提供了 13 个函数，很多函数的功能是重复的。这里只介绍最基本的函数 dijkstra_path() 和 dijkstra_path_length()。

3.1 dijkstra_path() 和 dijkstra_path_length() 使用说明

dijkstra_path() 用于计算从源到目标的最短加权路径，dijkstra_path_length() 用于计算从源到目标的最短加权路径长度。

dijkstra_path(G, source, target, weight=‘weight’)
dijkstra_path_length(G, source, target, weight=‘weight’)

主要参数：

G(NetworkX graph)：图。
source (node)：起点。
target (node)：终点。
weight (string or function)：参数为字符串(string)时，按该字符串查找边的属性作为权重；如果该字符串对应的边属性不存在，则权重置为1；参数为函数时，边的权重是函数的返回值。

返回值：

dijkstra_path() 的返回值是最短加权路径中的节点列表，数据类型为list。
dijkstra_path_length() 的返回值是最短加权路径的长度（路径中的边的权重之和）。

3.2 例题 1：无向图的最短路径问题

例题 1：已知如图的有权无向图，求顶点 v1 到顶点 v11 的最短路径。

本问题来自：司守奎、孙兆亮，数学建模算法与应用（第2版），P43，例4.3，国防工业出版社。

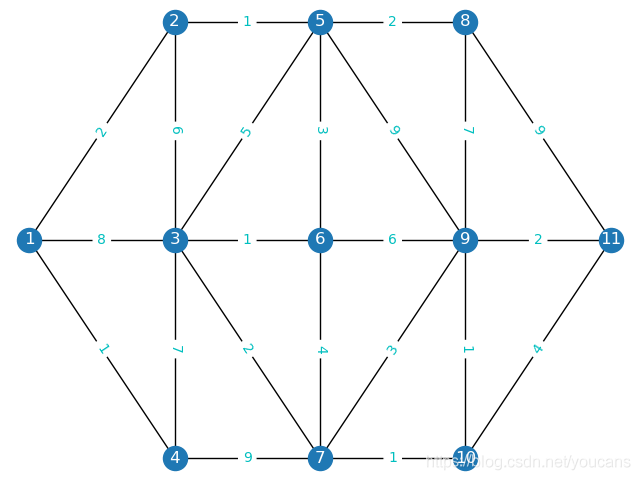
在这里插入图片描述

程序说明：

图的输入。本例的问题是稀疏的有权无向图，使用 add_weighted_edges_from() 函数可以用列表形式向图中添加多条赋权边，每个赋权边以元组 (node1,node2,weight) 表示。
图的绘制。使用 nx.draw() 绘图时，默认的顶点位置可能并不理想，可以通过 pos 指定顶点位置。
绘制边的属性。使用 nx.draw_networkx_edge_labels() 可以绘制边的属性，例程中选择显示权重属性。
使用 dijkstra_path() 和 dijkstra_path_length() 求指定顶点之间的最短加权路径和最短加权路径长度。

3.3 dijkstra_path() 算法例程

# mathmodel16_v1.py
# Demo16 of mathematical modeling algorithm
# Demo of shortest path with NetworkX
# Copyright 2021 YouCans, XUPT
# Crated：2021-07-07import matplotlib.pyplot as plt # 导入 Matplotlib 工具包
import networkx as nx  # 导入 NetworkX 工具包# 问题 1：无向图的最短路问题（司守奎，数学建模算法与应用，P43，例4.3）
G1 = nx.Graph()  # 创建：空的 无向图
G1.add_weighted_edges_from([(1,2,2),(1,3,8),(1,4,1),(2,3,6),(2,5,1),(3,4,7),(3,5,5),(3,6,1),(3,7,2),(4,7,9),(5,6,3),(5,8,2),(5,9,9),(6,7,4),(6,9,6),(7,9,3),(7,10,1),(8,9,7),(8,11,9),(9,10,1),(9,11,2),(10,11,4)])  # 向图中添加多条赋权边: (node1,node2,weight)
print('nx.info:',G1.nodes)  # 返回图的基本信息# 两个指定顶点之间的最短加权路径
minWPath_v1_v11 = nx.dijkstra_path(G1, source=1, target=11)  # 顶点 1 到 顶点 11 的最短加权路径
print("顶点 v1 到 顶点 v11 的最短加权路径: ", minWPath_v1_v11)
# 两个指定顶点之间的最短加权路径的长度
lMinWPath_v1_v11 = nx.dijkstra_path_length(G1, source=1, target=11)  # 最短加权路径长度
print("顶点 v1 到 顶点 v11 的最短加权路径长度: ", lMinWPath_v1_v11)pos = {1: (0,4), 2: (5,7), 3: (5,4), 4: (5,1), 5: (10,7), 6: (10,4), 7: (10,1),8: (15,7), 9: (15,4), 10: (15,1), 11: (20,4)}  # 指定顶点位置
labels = nx.get_edge_attributes(G1, 'weight')  # 设置边的 labels 为 ‘weight'
nx.draw(G1, pos, with_labels=True, font_color='w')  # 绘制无向图
nx.draw_networkx_edge_labels(G1, pos, edge_labels=labels, font_color='c')  # 显示边的权值
plt.show()

3.4 程序运行结果

nx.info: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
顶点 v1 到 顶点 v11 的最短加权路径:  [1, 2, 5, 6, 3, 7, 10, 9, 11]
顶点 v1 到 顶点 v11 的最短加权路径长度:  13

4. NetworkX 中的 Bellman-Ford 算法

NetworkX 中关于 Bellman-Ford 算法提供了多个函数，这里只介绍最基本的函数 bellman_ford_path() 和 bellman_ford_path_length()。

4.1 bellman_ford_path() 和 bellman_ford_path_length() 使用说明

bellman_ford_path() 用于计算从源到目标的最短加权路径，bellman_ford_path_length() 用于计算从源到目标的最短加权路径长度。

bellman_ford_path(G, source, target, weight=‘weight’)
bellman_ford_path_length(G, source, target, weight=‘weight’)

主要参数：

G(NetworkX graph)：图。
source (node)：起点。
target (node)：终点。
weight (string)：按字符串查找边的属性作为权重。默认值为权重 ‘weight’。

返回值：

bellman_ford_path() 的返回值是最短加权路径中的节点列表，数据类型为list。
bellman_ford_path_length() 的返回值是最短加权路径的长度（路径中的边的权重之和）。

4.2 例题 2：城市间机票价格问题

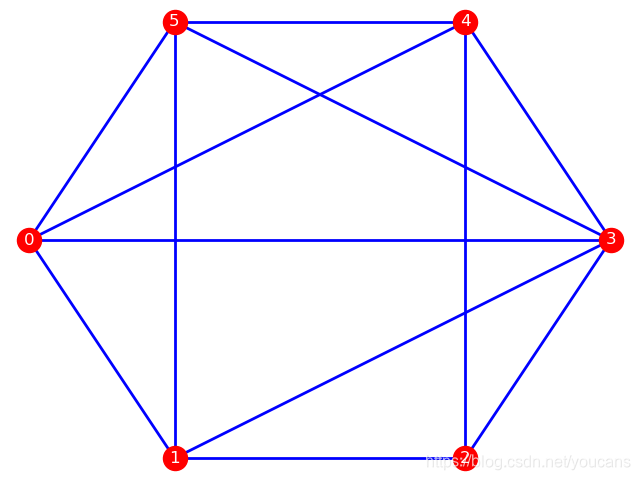
例题 2：城市间机票价格问题。

已知 6个城市之间的机票票价如矩阵所示（无穷大表示没有直航），求城市 c0 到其它城市 c1…c5 的票价最便宜的路径及票价。

$[050∞4025105001520∞25∞1501020∞4020100102525∞20100551025∞25550]\begin{bmatrix} 0 & 50 & \infty & 40 & 25 & 10\\ 50 & 0 & 15 & 20 & \infty & 25\\ \infty & 15 & 0 & 10 & 20 & \infty\\ 40 & 20 & 10 & 0 & 10 & 25\\ 25 & \infty & 20 & 10 & 0 & 55\\ 10 & 25 & \infty & 25 & 55 & 0\\ \end{bmatrix}$
本案例问题改编自：司守奎、孙兆亮，数学建模算法与应用（第2版），P41，例4.1，国防工业出版社。

程序说明

图的输入。使用 pandas 中 DataFrame 读取数据文件非常方便，本例中以 pandas 输入顶点邻接矩阵，使用 nx.from_pandas_adjacency(dfAdj) 转换为 NetworkX 的图。
邻接矩阵。邻接矩阵 dfAdj (i,j) 的值表示连接顶点 i、j 的边的权值， dfAdj (i,j) = 0 表示 i、j 不相邻，本例中表示没有直航。
最短路径与最短路径长度。nx.shortest_path() 返回最短路径。nx.shortest_path_length() 返回最短路径长度，本例中可以理解为从起点到终点的乘机次数：1 表示直航，2 表示中转一次。
最短加权路径长度。nx.bellman_ford_path_length() 返回最短加权路径长度，本例中权重为票价，最短加权路径长度即为两点间最便宜的直航或中转的机票票价。
通过本案例，可以直观地理解最短路径长度与最短加权路径长度的区别。

4.3 bellman_ford_path() 算法例程

# mathmodel16_v1.py
# Demo16 of mathematical modeling algorithm
# Demo of shortest path with NetworkX
# Copyright 2021 YouCans, XUPT
# Crated：2021-07-07import pandas as pd
import matplotlib.pyplot as plt # 导入 Matplotlib 工具包
import networkx as nx  # 导入 NetworkX 工具包# 问题 2：城市间机票价格问题（司守奎，数学建模算法与应用，P41，例4.1）
# # 从Pandas数据格式（顶点邻接矩阵）创建 NetworkX 图
# # from_pandas_adjacency(df, create_using=None) # 邻接矩阵，n行*n列，矩阵数据表示权重
dfAdj = pd.DataFrame([[0, 50, 0, 40, 25, 10],  # 0 表示不邻接，[50, 0, 15, 20, 0, 25],[0, 15, 0, 10, 20, 0],[40, 20, 10, 0, 10, 25],[25, 0, 20, 10, 0 ,55],[10, 25, 0, 25, 55, 0]])
G2 = nx.from_pandas_adjacency(dfAdj)  # 由 pandas 顶点邻接矩阵 创建 NetworkX 图# 计算最短路径：注意最短路径与最短加权路径的不同
# 两个指定顶点之间的最短路径
minPath03 = nx.shortest_path(G2, source=0, target=3)  # 顶点 0 到 顶点 3 的最短路径
lMinPath03 = nx.shortest_path_length(G2, source=0, target=3)  #最短路径长度
print("顶点 0 到 3 的最短路径为：{}，最短路径长度为：{}".format(minPath03, lMinPath03))
# 两个指定顶点之间的最短加权路径
minWPath03 = nx.bellman_ford_path(G2, source=0, target=3)  # 顶点 0 到 顶点 3 的最短加权路径
# 两个指定顶点之间的最短加权路径的长度
lMinWPath03 = nx.bellman_ford_path_length(G2, source=0, target=3)  #最短加权路径长度
print("顶点 0 到 3 的最短加权路径为：{}，最短加权路径长度为：{}".format(minWPath03, lMinWPath03))for i in range(1,6):minWPath0 = nx.bellman_ford_path(G2, source=0, target=i)  # 顶点 0 到其它顶点的最短加权路径lMinPath0 = nx.bellman_ford_path_length(G2, source=0, target=i)  #最短加权路径长度print("城市 0 到 城市 {} 机票票价最低的路线为: {}，票价总和为：{}".format(i, minWPath0, lMinPath0))nx.draw_shell(G2, with_labels=True, node_color='r', edge_color='b', font_color='w', width=2)
plt.show()

4.4 程序运行结果

顶点 0 到 3 的最短路径为：[0, 3]，最短路径长度为：1
顶点 0 到 3 的最短加权路径为：[0, 4, 3]，最短加权路径长度为：35
城市 0 到 城市 1 机票票价最低的路线为: [0, 5, 1]，票价总和为：35
城市 0 到 城市 2 机票票价最低的路线为: [0, 4, 2]，票价总和为：45
城市 0 到 城市 3 机票票价最低的路线为: [0, 5, 3]，票价总和为：35
城市 0 到 城市 4 机票票价最低的路线为: [0, 4]，票价总和为：25
城市 0 到 城市 5 机票票价最低的路线为: [0, 5]，票价总和为：10

在这里插入图片描述

5. 总结

最短路径问题是图论研究中的经典算法问题，用于计算图中一个顶点到另一个顶点的最短路径。
在图论中，求最短路径长度是要计算从起点到终点步数最少的路径，而求最短路径距离是要计算最短加权路径长度。从例 2的运行结果可以对比二者的区别。
求最短路径长度的常用算法是 Dijkstra 算法、Bellman-Ford 算法和Floyd 算法，另外还有启发式算法 A*。
对于稀疏的图推荐使用列表形式添加赋权边，对于稠密图、完全图建议使用 DtaFrame 读取数据文件后再转换为 NetworkX 格式。

【本节完】

欢迎关注『Python小白的数学建模课 @ Youcans』原创作品

原创作品，转载必须标注原文链接：(https://blog.csdn.net/youcans/article/details/118555468)。

Crated：2021-07-07

欢迎关注『Python小白的数学建模课 @ Youcans』系列，持续更新
Python小白的数学建模课-01.新手必读
Python小白的数学建模课-02.数据导入
Python小白的数学建模课-03.线性规划
Python小白的数学建模课-04.整数规划
Python小白的数学建模课-05.0-1规划
Python小白的数学建模课-06.固定费用问题
Python小白的数学建模课-07.选址问题
Python小白的数学建模课-09.微分方程模型
Python小白的数学建模课-10.微分方程边值问题
Python小白的数学建模课-12.非线性规划
Python小白的数学建模课-15.图论的基本概念
Python小白的数学建模课-16.最短路径算法
Python小白的数学建模课-17.条件最短路径算法
Python小白的数学建模课-18.最小生成树问题
Python小白的数学建模课-19.网络流优化问题
Python小白的数学建模课-20.网络流优化案例
Python小白的数学建模课-21.关键路径法
Python小白的数学建模课-A1.国赛赛题类型分析
Python小白的数学建模课-21.关键路径法
Python小白的数学建模课-22.插值方法
Python小白的数学建模课-A1.国赛赛题类型分析
Python小白的数学建模课-A2.2021年数维杯C题探讨
Python小白的数学建模课-A3.12个新冠疫情数模竞赛赛题及短评
Python小白的数学建模课-B2. 新冠疫情 SI模型
Python小白的数学建模课-B3. 新冠疫情 SIS模型
Python小白的数学建模课-B4. 新冠疫情 SIR模型
Python小白的数学建模课-B5. 新冠疫情 SEIR模型
Python小白的数学建模课-B6. 新冠疫情 SEIR改进模型