目录
1.计算样本相关系数和偏自相关系数
2.模型识别
模型定阶的困难
样本相关系数的近似分布及模型定阶经验方法
例题:
2.参数估计
常用估计方法:
1.矩估计
2.极大似然估计
3.最小二乘估计
R中,参数估计用arima函数
例题
小结
1.计算样本相关系数和偏自相关系数
样本自相关系数:

样本偏自相关系数:样本估计值加 ^ ,总体真实值没有哦!!
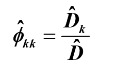
其中:
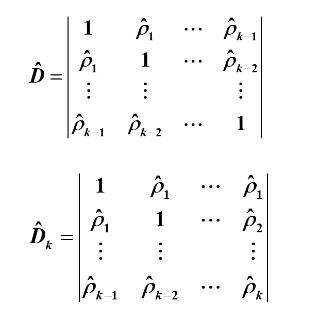
2.模型识别
基本原则:

由上方还可得到:

模型定阶的困难
由于样本的随机性,样本的相关系数不会呈现出理论截尾的完美情况,本应结尾的,
仍会呈现小值振荡。
平稳时间序列通常具有短期相关性,随着1延迟阶数,
与
都会衰减至0附近作小值波动。
样本相关系数的近似分布及模型定阶经验方法
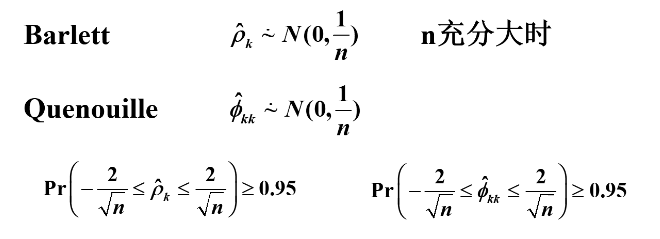
模型定阶的经验方法:
若样本(偏)自相关系数在最初的d阶明显大于两倍标准差,而后几乎95%都落在2倍标准差内,且通常由非零自相关系数衰减为小值波动的过程非常突然。通常视(偏)自相关系数截尾。截尾阶数为d。
例题:
检验过程:

例4-1选择合适的模型拟合1900- 1998年全球7级以上地震发生次数序列。
a<-read.table("C:/Users/zyj/Desktop/4_1.csv",sep=",",header=T)
x<-ts(a$number,start=1900)
plot(x) #时序图
#library(aTSA) #aTSA导入程序包
adf.test(x) #单位根检验
for(i in 1:2)print(Box.test(x,lag=6*i))
acf(x)
pacf(x)返回:
时序图:初步观察,该序列是平稳的,因在一个常数范围内摆动,但有一定的主观性

单位根检验:
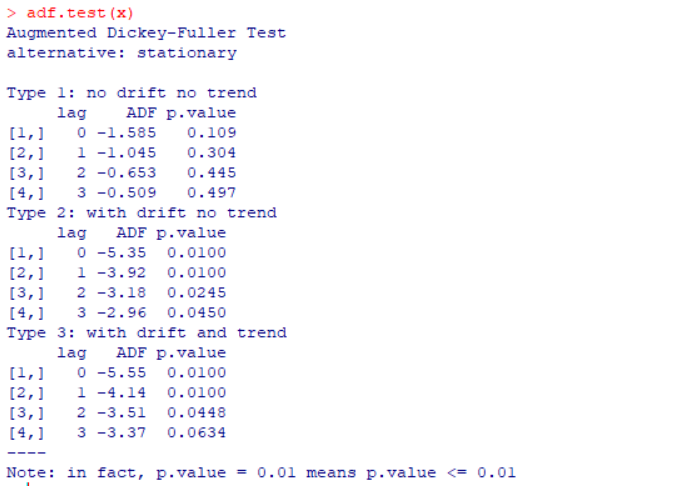
type1中p值都大于0.05,所以非平稳;type2中p值都小于0.05,所以平稳;type3中只有在延迟期数为0,1,2中的p值都小于0.05,所以在延迟期数为0,1,2上平稳,3以后非平稳。
白噪声检验:

如图,延迟6期和12期的p值都小于0.05,所以不是白噪声序列。
综上,该序列是平稳的非白噪声序列。
自相关系数图:

如图,从5阶开始才进入二倍标准差区间,所以具有拖尾性。
偏自相关系数图:

如图,从2阶开始突然全部在二倍标准差区间内,所以具有1阶截尾性。
综上,由自相关系数和偏自相关系数是AR(1)模型
例4-2选择合适的模型拟合美国科罗拉多州某一加油站连续57天的盈亏(OVERSHORT)序列
b<-read.table("C:/Users/zyj/Desktop/4_2.csv",sep=",",header=T)
y<-ts(b$overshort)
plot(y) #时序图
#library(aTSA) #aTSA导入程序包
adf.test(y) #单位根检验
for(i in 1:2)print(Box.test(y,lag=6*i))
acf(y)
pacf(y)返回:
时序图:
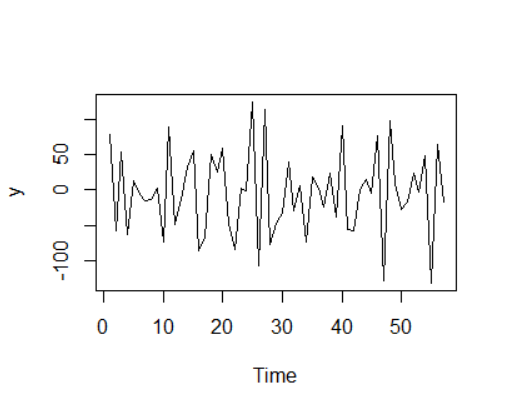
如图,很明显是平稳的。再进行一下单位根检验。
单位根检验:
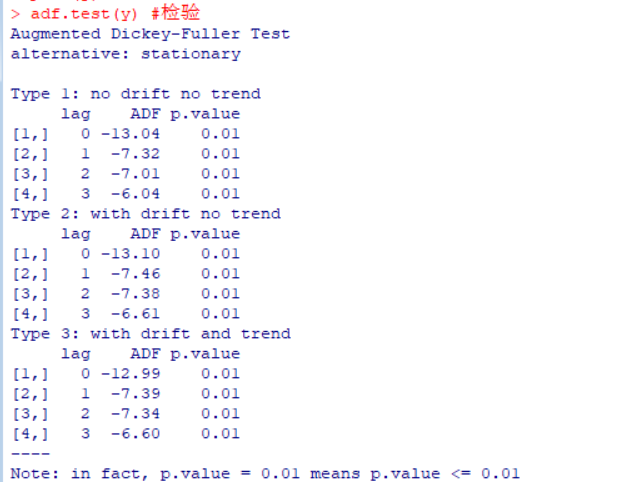
如图,所有类型的p值都小于0.05,所以拒绝原假设,认为它是平稳序列。
白噪声检验:
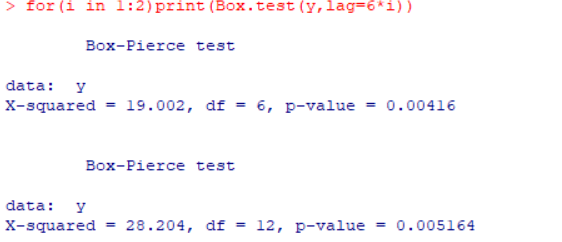
如图,延迟6期和12期的p值都小于0.05,所以不是白噪声序列。
自相关系数图:
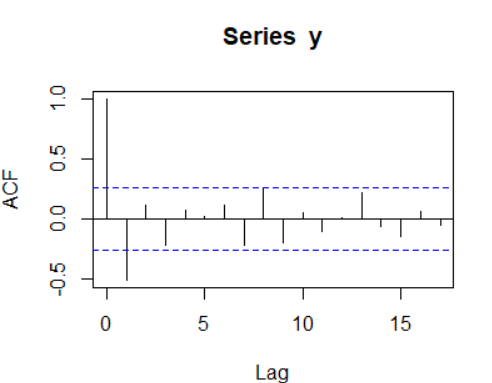
如图,,从2阶开始基本都在二倍标准差区间内,所以是1阶截尾。
偏自相关系数图:
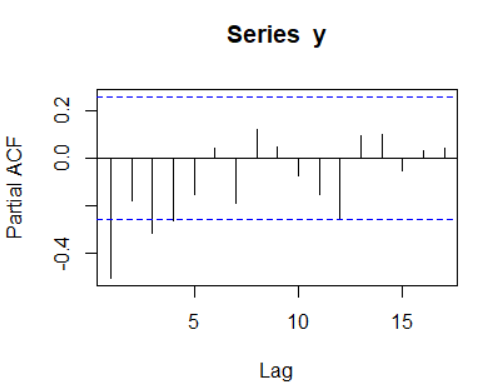
如图,具有拖尾性。
综上,该模型为MA(1)模型。
例4-3选择合适的模型拟合1880-1985全球气表平均温度改变值差分序列(表例4-3.csv中全球气表平均温度改变值序列)
c<-read.table("D:/桌面/4_3.csv",sep=",",header=T)
z<-ts(c$change,start=1880)
plot(z) #时序图
difz<-diff(z)
plot(difz) #差分时序图
#library(aTSA) #aTSA导入程序包
adf.test(difz) #单位根检验
for(i in 1:2)print(Box.test(difz,lag=6*i))
acf(difz)
pacf(difz)返回:
时序图:
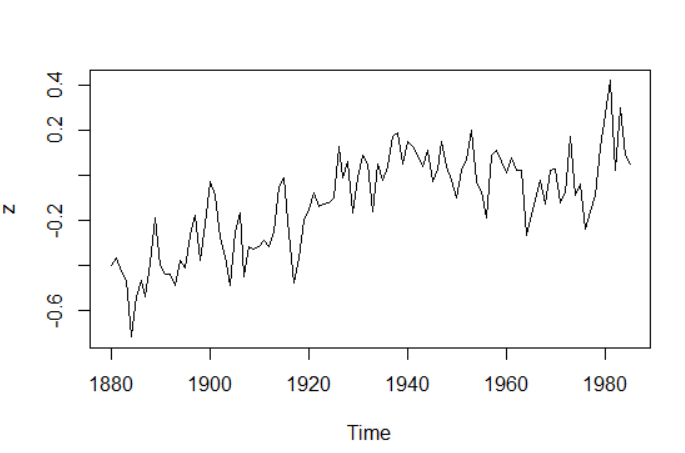
如图,有上升的趋势,所以不是平稳的
差分时序图:
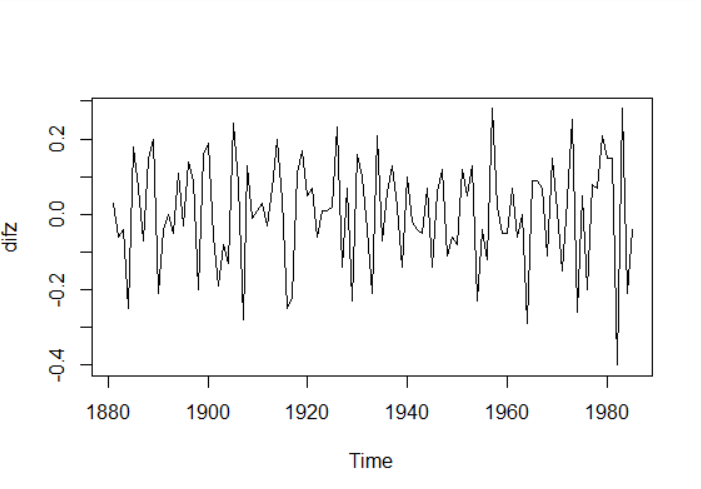
如图,可得是平稳的,但还需检验
对差分进行检验:
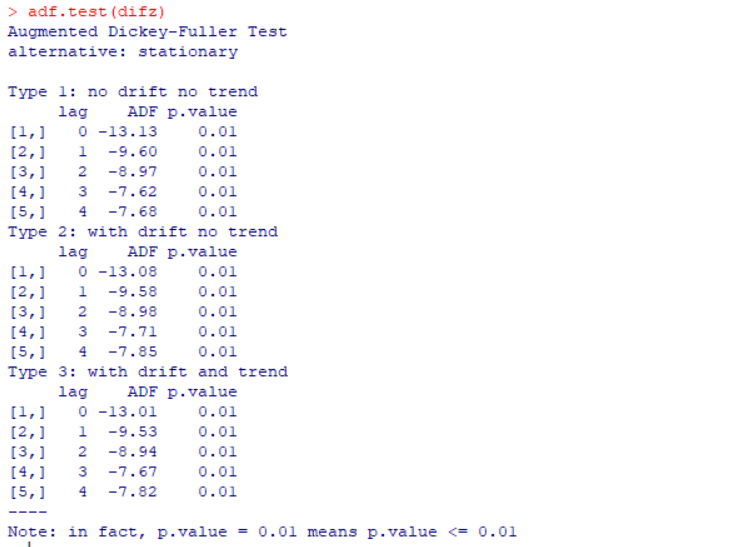
如图,各属性的p值都小于0.05,所以拒绝原假设,认为它是平稳的。
白噪声检验:

如图,延迟6期和12期的p值都小于0.05,所以不是白噪声序列
自相关系数图:
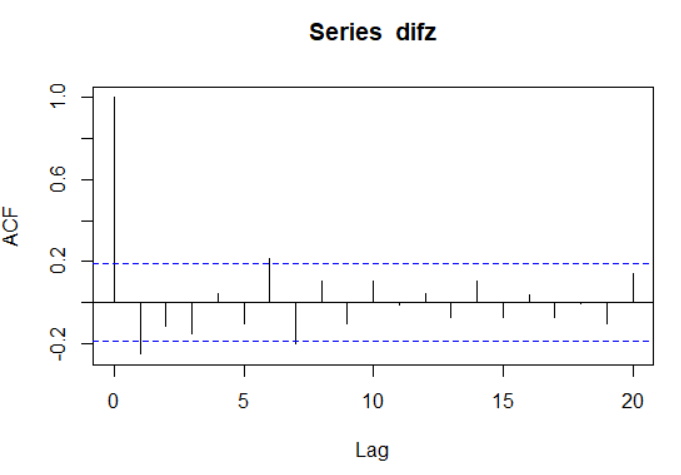
如图,具有拖尾性
偏自相关系数图:
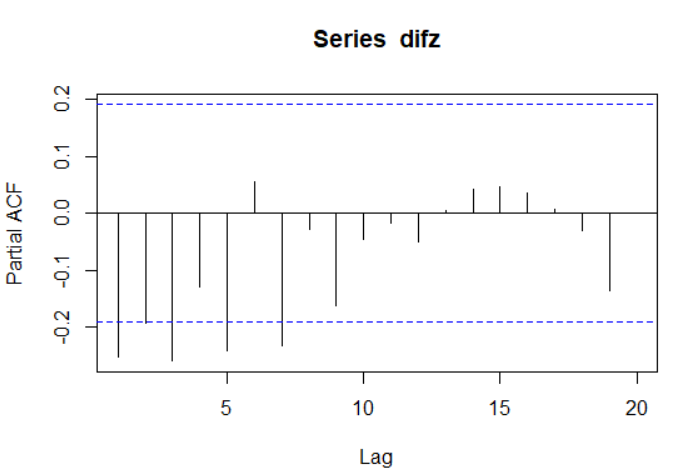
如图,在7阶以后才逐渐进入二倍标准差区间,所以具有拖尾性
综上,该模型是ARMA(1,1)模型
2.参数估计
对于一个非中心化ARMA(p,q)模型

常用估计方法:
- 距估计
- 极大似然估计
- 最小二乘估计
1.矩估计
原理:样本自相关系数估计总体自相关系数

样本一阶均值估计总体均值,样本方差估计总体方差
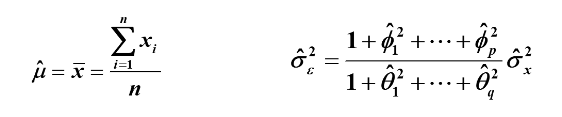
对矩估计的评价:
优点:
●估计思想简单直观
●不需要假设总体分布
●计算量小(低阶模型场合)
缺点:
●信息浪费严重:只用到了p+q个样本自相关系数信息,其他信息都被忽略.
●估计精度差
通常矩估计方法被用作极大似然估计和最小二乘估计迭代计算的初始值
2.极大似然估计
原理:样本出现概率最大。因此未知参数的极大似然估计就是使得似然函数(即联合密度函数)达到最大
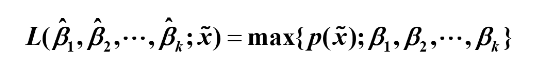
设序列服从多元正态分布:
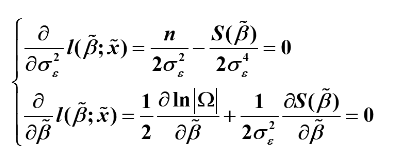
似然方程组是由p+q+1个超越方程构成,通常需要经过复杂的迭代算法才能求出
对极大似然估计的评价:
优点
●极大似然估计充分应用了每一个观察值所提供的信息,因而它的估计精度高
●同时还具有估计的一致性、渐近正态性和渐近有效性等许多优良的统计性质.
缺点
●需要假定总体分布
3.最小二乘估计
原理:使残差平方和达到最小的那组参数值即为最小二乘估计值
![]()
条件最小二乘估计
假设条件:假设过去未观测到的序列值等于零=0,1≤0
通过迭代求解
对最小二乘估计的评价:
优点
●最小二乘估计充分应用了每一个观察值所提供的信息,因而它的估计精度高
●条件最小二乘估计方法使用率最高
缺点
●需要假定总体分布
R中,参数估计用arima函数

例题
例4-1续(1)使用极大似然估计法确定1900-1998年全球7级以上地震发生次数序列拟合模型的口径。
拟合模型: AR(1)

R拟合:
fit1=arima(x,order=c(1,0,0),method="ML")
fit1返回:

例4-2续(1)确定美国科罗拉多州某一加油站连续57天盈亏序列拟合模型的口径
拟合模型: MA(1)
估计方法:条件最小二乘法估计
模型口径:
![]()
![]()
R拟合:
fit2=arima(y,order=c(0,0,1),method="CSS")
fit2返回:

例4-3续(1)确定1880-1985全球气表平均温度改变值差分序列拟合模型的口径
拟合模型:ARMA(1,1)
估计方法:条件最小二乘与极大似然混合估计模型口径
模型口径:
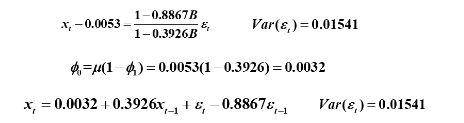
R拟合:
fit3<-arima(difz,order=c(1,0,1))
fit3返回:

小结
1、参数估计
矩估计、极大似然估计、最小二乘估计
2、R实现
arima(x,order=,include.mean=,method=)



















 dtype()