limx→+∞(1+1x)x2ex\lim_{x \to + \infty}\frac{(1+\frac{1}{x})^{x^2}}{e^x} x→+∞limex(1+x1)x2
正确的解法:

一种错误的解法:

这是同学问我的,错在了哪里?
limx→+∞(1+1x)x2是否可以等于limx→∞ex?\lim_{x \to + \infty}(1+\frac{1}{x})^{x^2}是否可以等于\lim_{x \to \infty}e^x?limx→+∞(1+x1)x2是否可以等于limx→∞ex?

实际上limx→+∞(1+1x)x2可以等于limx→∞ex\lim_{x \to + \infty}(1+\frac{1}{x})^{x^2}可以等于\lim_{x \to \infty}e^xlimx→+∞(1+x1)x2可以等于limx→∞ex,依据就是复合函数的极限
这个东西可以这么做题,如
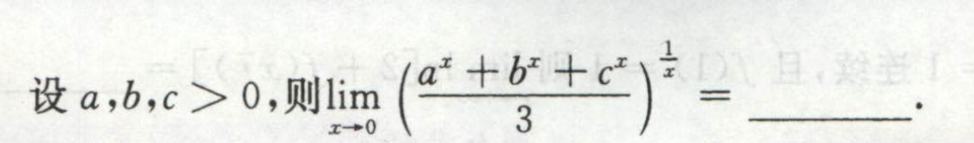


而之前求极限错误是在于极限相除的条件是上面和下面的极限都要存在,明显上下极限都不存在,所以就没法这么用了
(不是说都不存在才没法这么用,定理三是这么讲的

一些同学在做题的时候,简单地认为下面等式左右是相等的
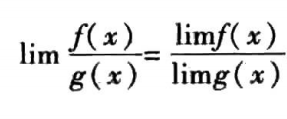
却忽视了前提条件
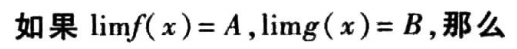
)









)
:OSM数据获取)



静态ip配置(桥接模式))




