在前面我讲解了如何通过最长公共子串来求解两个文本的相似度问题，但它有一定缺陷，举个例子，看下面的两个字符串

我爱吃小青菜和各种鲜水果。

我很爱吃青菜与各样水果。

上面两个字符串，如果通过计算子串来求相似度，会发现相似度比较低，但如果考虑用最长公共子序列算法求相似度问题，则相似度会很高。子串是有序且连续的，而子序列是有序但不一定连续。

那么，本文就来讲讲如何求两个字符串的最长公共子序列。

一. 暴力解法

跟求最长公共子串一样，也可以用暴力方法来求解最长公共子序列问题，但是复杂度会更高，时间复杂度是指数级别的，很显然，这种方法行不通。

二. 动态规划法

假如两个字符串分别表示为X=[x_0, x_1, ..., x_m-1]，Y=[y_0, y_1, ..., y_n-1]，通过动态规划法求最长公共子序列，那么用dp[i][j]来表示以x_i和y_j为结尾的最长公共子串的长度，那么

1. 当x_i=y_j时，dp[i][j] = dp[i - 1][j - 1] + 1
2. 当x_i≠y_j时，dp[i][j]为dp[i - 1][j]和dp[i][j - 1]中最大的那个

所以得到其状态转移方程如下

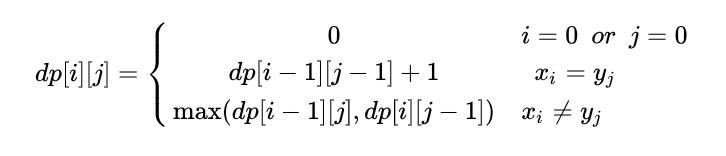
代码如下

int LCS(string x, string y) { int xlen = x.size(); int ylen = y.size(); for (int i = 0; i <= xlen; i++) { for (int j = 0; j <= ylen; j++) { if (i == 0 || j == 0) { dp[i][j] = 0; } else if (x[i - 1] == y[j - 1]) { dp[i][j] = dp[i - 1][j - 1] + 1; } else { dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]); } } } return dp[xlen][ylen];}

很明显，基于动态规划法的最长公共子序列的时间复杂度为O(mn)。

后面会讲解更多关于求解文本相似度问题的算法，欢迎大家的关注！