BP算法和RNN_模型CNN-RNN-LSTM和GRU简介

深度学习自从2006年以后已经“火”了十多年了，目前大家看到的，最普遍的应用成果是在计算机视觉、语音识别和自然语言处理（NLP）。最近工业界也在努力地扩展它的应用场景，比如游戏、内容推荐和广告匹配等等。

深度模型架构分三种：

前向反馈网络：MLP，CNN；
后向反馈网络：stacked sparse coding, deconvolutional nets；
双向反馈网络：deep Boltzmann machines, stacked auto-encoders。

卷积神经网络(Convolutional Neural Network, CNN) 应该是最流行的深度学习模型，在计算机视觉也是影响力最大的。下面介绍一下深度学习中最常用的CNN模型，以及相关的RNN模型，其中也涉及到著名的LSTM和GRU。

基本概念

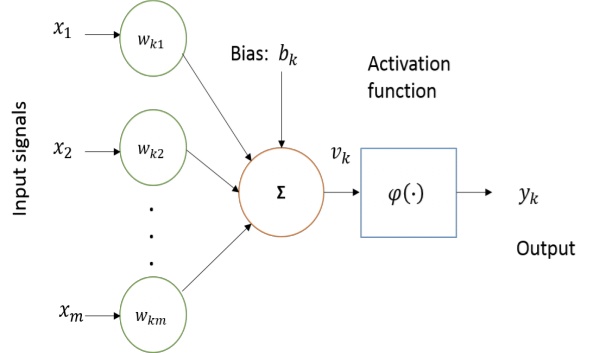
计算神经生物学对构建人工神经元的计算模型进行了重要的研究。试图模仿人类大脑行为的人工神经元是构建人工神经网络的基本组成部分。基本计算元素（神经元）被称为节点（或单元），其接收来自外部源的输入，具有产生输出的一些内部参数（包括在训练期间学习的权重和偏差）。这个单位被称为感知器。感知器的基本框图如下图所示。

图显示神经元的基本非线性模型，其中 1， 2， 3，... 是输入信号; 1， 2， 3，⋯ 是突触权重; 是输入信号的线性组合; φ（∙）是激活函数（例如sigmoid），是输出。偏移与输出的线性组合器相加，具有应用仿射变换的效果，产生输出。神经元功能可以用数学表示如下：

神经元的基本模型

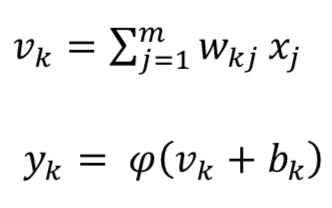
人工神经网络或一般神经网络由多层感知器（MLP）组成，其中包含一个或多个隐藏层，每层包含多个隐藏单元（神经元）。具有MLP的NN模型如图所示。

带有MLP的NN模型

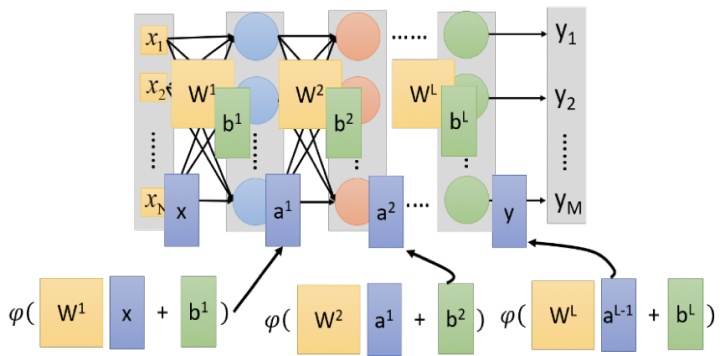
多层感知器输出

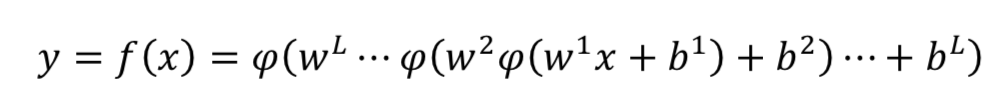
学习率（learning rate）是训练DNN的重要组成部分。它是训练期间考虑的步长，使训练过程更快。但是，选择学习率是敏感的。如果为η较大，网络可能会开始发散而不是收敛；另一方面，如果η选择较小，则网络需要更多时间收敛。此外它可能很容易陷入局部最小值。

有三种常用方法可用于降低训练期间的学习率：常数、因子和指数衰减。首先，可以定义一个常数ζ，基于定义的步长函数手动地降低学习率。其次，可以在训练期间根据以下等式调整学习率：

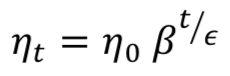
指数衰减的步进函数格式为：

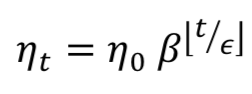
梯度下降法是一阶优化算法，用于寻找目标函数的局部最小值。算法1解释了梯度下降的概念：

算法1 梯度下降

输入：损失函数ε，学习率η，数据集，和模型F（θ，）

输出：最小化ε的最优θ

重复直到收敛：

结束

由于训练时间长是传统梯度下降法的主要缺点，因此随机梯度下降（Stochastic Gradient Descent ，SGD）方法用于训练深度神经网络（DNN）。算法2详细解释了SGD。

算法2 随机梯度下降

输入：损失函数ε，学习率η，数据集，和模型F（θ，）

输出：最小化ε的最优θ

重复直到收敛：

随机（，）;

对于（，）的每批（ i， i）做

结束

深度NN使用流行的反向传播（BP）算法和SGD 进行训练。算法3给出了基本BP的伪代码。在MLP的情况下，可以容易地用有向非循环图（directive acyclic graphs）这样的计算图来表示NN模型。DL的表示，如算法3所示，让一个单路径网络使用链规则有效地计算从顶层到底层的梯度。

算法3 BP算法

输入：具有层的网络，激活函数σ ，

隐藏层的输出

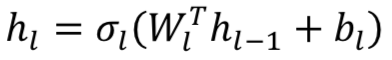
和网络输出

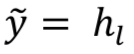
计算梯度：

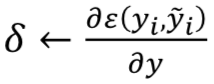
从 ← 到0做

计算当前层的梯度：

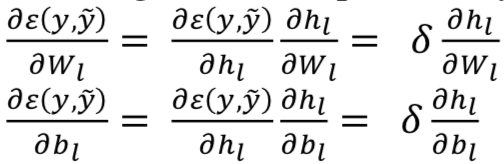
用

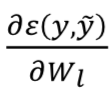
和

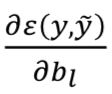
应用梯度下降（GD）

反向传播（BP）梯度到下一层

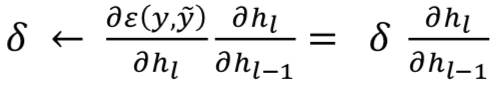
结束

动量（Momentum）是一种有助于SGD加速训练的方法。它背后的主要思想是使用梯度的移动平均值，而不是仅使用梯度的当前实际值。其数学表达如以下等式：

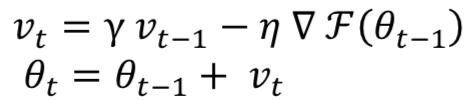
这里γ是动量，η是第t轮训练的学习率。在训练期间使用动量的主要优点是防止网络卡在局部最小值。动量值为γ∈（0,1）。较高的动量值超过其最小值，可能使网络不稳定。通常γ设置为0.5，直到初始学习稳定，然后增加到0.9 或更高。

权重衰减（Weight decay）用于训练深度学习模型作为L2正则化方法，这有助于防止过度拟合网络和模型泛化。 F（θ，）的L2正则化可以定义为：

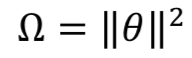
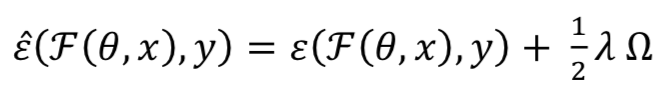
权重的梯度是

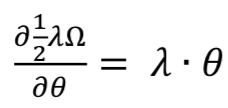
其中 = 0.0004。

批处理归一化（BN）通过输入样本移位来减少内部协方差，从而加速DL过程。这意味着输入被线性转换为零均值和单位方差。对于白化的输入，网络收敛速度更快，并且在训练期间表现出更好的正则化，这对整体精度有影响。由于数据白化是在网络外执行的，在模型训练期间不会产生白化的影响。在深度递归神经网络（RNN），第n层的输入是第n-1层的组合，不是原始特征输入。随着训练的进行，归一化或白化的效果分别降低，这导致梯度消失（vanishing gradient）问题。这可能会减慢整个训练过程并导致饱和（saturation）。为了更好地训练，BN应用于深度神经网络的内部层。这种方法确保了理论上和基准测试（benchmarks）实验中更快的收敛。在BN中，一层的特征独立地归一化为均值零和方差1。BN的算法在算法4中给出。

算法4 BN

输入：小批量（mini-batch）x值： = { 1,2,3......， }

输出：{yi = BNγ，β（xi）}

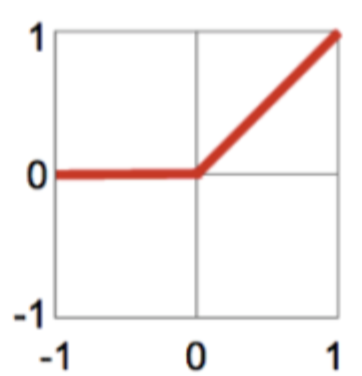
激活函数如下：如图所示

（a）sigmoid （b）双曲正切

（c）ReLU

（d）Leaky ReLU （e）Exponential Linear Unit (ELU)

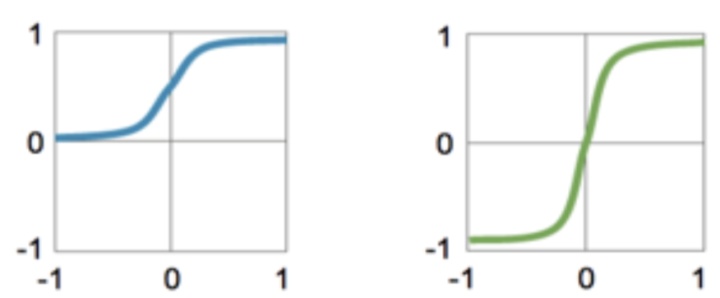
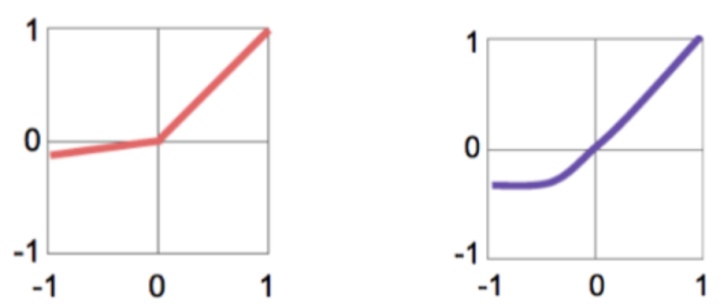
Sigmoid

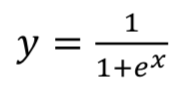
TanH

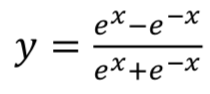
Rectified Linear Unit (ReLU)： y = max（x，0）
Leaky ReLU： y = max（x，ax）
Exponential Linear Unit (ELU)：

卷积神经网络（CNN）

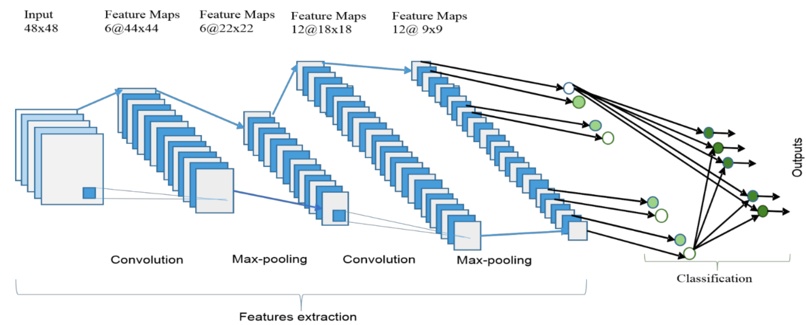
如图显示了一个CNN的整体架构，包括两个主要部分：特征提取和分类器。在特征提取层，网络的每一层都接收来自其前一层的输出作为其输入，并将其输出作为输入传递给下一层。这个CNN架构由三种类型层组合而成：卷积（convolution），最大池化（max-pooling）和分类（classification）。在网络的低层和中层有两种类型的层：卷积层和最大池化层。偶数层用于卷积，奇数层用于最大池化操作。卷积和最大池化层的输出节点组合成为一个2D平面，叫特征图（feature map）。一个层的每个平面通常由前层一个或多个平面的组合导出。平面的节点连接到前一层每个连接平面的小区域。卷积层的每个节点通过卷积运算从输入图像中提取特征。CNN的整体架构包括输入层、多个交替的卷积层和最大池化层、一个全连接层和一个分类层。

CNN

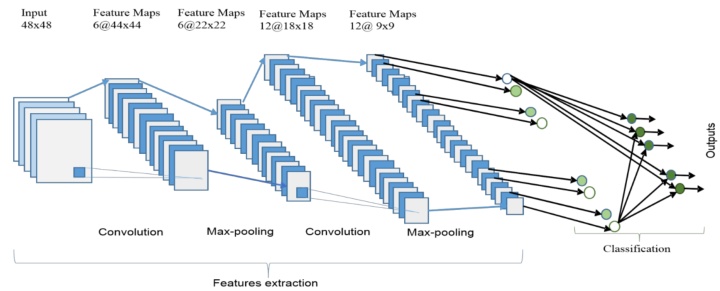
更高级的特征来自从较低层传播的特征。随着特征传播到最高层或级别，特征的维度减小分别取决于卷积和最大池化操作的内核大小。然而，为了确保分类准确性，通常增加特征图的数量代表更好的输入图像特征。CNN的最后一层输出作为全连接网络的输入，该网络称为分类层。前馈神经网络已被用作分类层。

相对于最终神经网络权重矩阵的维度，期望数量的特征选择在分类层中作为输入。然而，就网络或学习参数而言，全连接层是昂贵的。有几种技术，包括平均池化和全局平均池化，作全连接网络的替代方案。在顶部分类层中softmax层计算相关类别的得分。分类器选最高分输出相关类别。

卷积层

在此层，先前层的特征图与可学习的内核进行卷积。内核的输出经过线性或非线性激活函数，例如sigmoid、双曲正切（hyperbolic tangent）、softmax，整流线性（rectified linear）和标识（identity）函数，生成输出特征图。每个输出特征图可以与多个输入特征图组合。总的来说，有

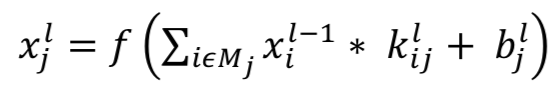
其中是当前层输出， -1是前一层输出，是当前层内核，是当前层的偏差。代表选择的输入地图。对于每个输出图，给出了附加偏差。但是，输入图将与不同的内核进行卷积生成相应的输出图。

池化层

亚采样层对输入图执行下采样操作，这通常称为池化层。在此层中，输入和输出特征图的数量不会更改。例如，如果有输入映射，那么将会有完全输出映射。由于下采样操作，输出图每个维度大小都减小，这取决于下采样掩码大小。例如：如果使用2×2下采样内核，则所有图像输出维度将是相应输入图像维度的一半。该操作可以表述为

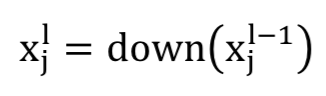
在该层中主要执行两种类型的操作：平均池化或最大池化。在平均池化方法，函数通常总结来自前一层的特征图的N×N个补丁并选择平均值。在最大池化，从特征图的N×N个补丁中选择最高值。因此，输出地图尺寸减少n次。特殊情况下，输出图乘以一个标量。已经有一些替代的亚采样层，例如分数最大池化（fractional max pooling）层和带卷积的亚采样。

分类层

这是全连接层，根据前面卷积层提取的特征计算每个类的得分。最终的层特征图表示为一组标量数值的矢量，这些标量值传递到全连接层。全连接前馈神经层作为softmax分类层。

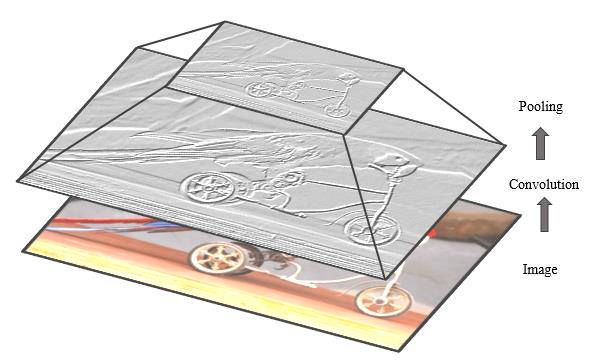
在CNN的反向传播（BP）中，全连接层按照全连接神经网络（FCNN）的方法更新。在卷积层和其前一层之间对特征图执行全卷积运算来更新卷积层的滤波器。如图显示了输入图像的卷积和亚采样等基本操作。

卷积和池化

网络参数和内参需求

计算参数的数量是衡量深度学习模型复杂性的重要指标。输出特征图的大小

=（ - ）/ +1

其中是指输入特征图的尺寸，是指滤波器或感受野（receptive field）的尺寸，是指输出特征图的尺寸，代表步幅（stride）。填充（padding）通常在卷积应用，以确保输入和输出特征图具有相同的尺寸。填充尺寸取决于内核的大小。填充的行数和列数如下：

=（ - 1）/ 2

这里是填充尺寸，是内核维度。有几个标准考虑来比较模型。但是，大多数情况下会考虑网络参数的数量和内存需求。第层的参数（）量计算按以下等式：

=（ × × -1）×

如果偏移与权重参数相加，则上述等式可重写：

=（ ×（ +1）× -1）×

这里第层的参数总数记为，是输出特征图的总数， -1是输入特征图或通道的总数。例如，假设第层具有 -1 = 32个输入特征图， = 64个输出特征图，并且滤波器大小为 = 5，在这种情况下，该层的偏移参数总数为

=（5×5×33）× 64 = 528,000

因此，第层操作所需的内存大小（）可以表示为

=（ × × ）

递归神经网络（RNN）

RNN是唯一的，它允许随时间推移在一系列向量上进行操作。如图示意所示。

RNN基本架构

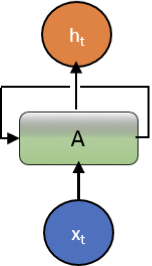
在Elman架构中，使用隐层的输出和隐层的正常输入一起作为输入。另一方面，Jordan网络中输出单元的输出作为隐藏层的输入。相反地Jordan使用输出单元的输出同时作为自身和隐藏层的输入。在数学上，可以表达为：

Elman网络

h = h( h + hh −1 + h)

= ( h + )

Jordan网络

h = h( h + h −1 + h)

= ( h + )

其中是输入向量, h 是隐层向量, 是输出向量, w和u是权重矩阵，b是偏移向量。

循环允许信息从网络的一个步骤传递到下一个步骤。可以将递归神经网络视为同一网络的多个副本，每个网络将消息传递给后继者。下图显示了如果循环展开（unroll the loop）会发生什么。

展开的RNN

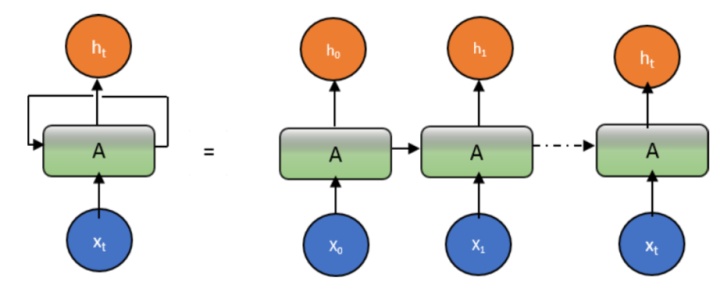
RNN方法的主要问题是梯度消失。

LSTM（Long Short Term Memory）

长短时记忆（LSTM，Long Short Term Memory）的关键思想是单元（cell）状态，如图水平线贯穿的顶部。LSTM将信息移除或添加到单元状态（cell state），称为门（gates）：输入门（），忘记门（）和输出门（）可以定义为如下公式：

LSTM

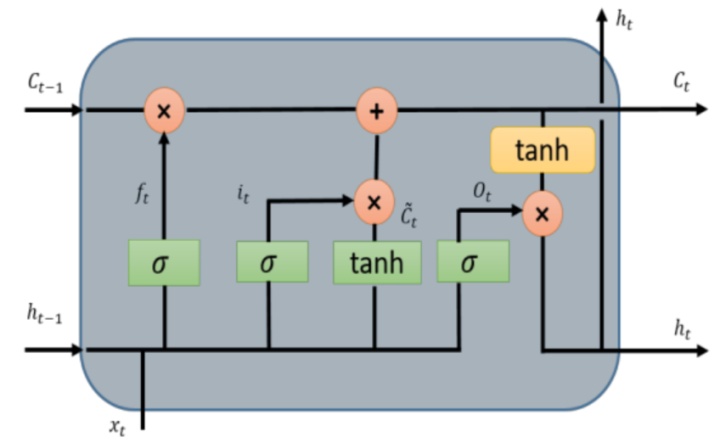
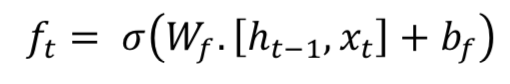
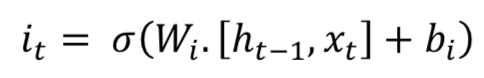
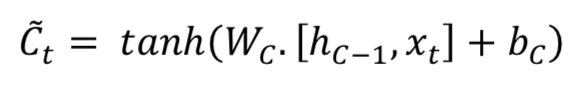
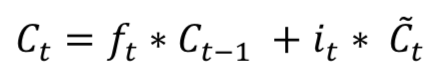
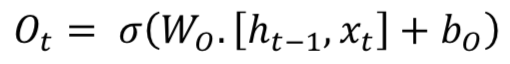
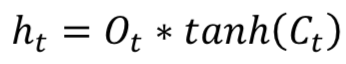
LSTM模型在时间信息处理中很受欢迎。大多数包含LSTM模型的论文都有一些微小的差异。

Gated Recurrent Unit (GRU)

门控递归单元（Gated Recurrent Unit，GRU) 也来自LSTMs。GRU受欢迎的主要原因是计算成本和模型的简单性，如图所示。在拓扑、计算成本和复杂性方面，GRU是比标准LSTM更轻的RNN版。该技术将遗忘门（forget gates）和输入门（input gates）组合成单个“更新门（update gate）”，并将单元状态、隐藏状态以及一些其他变化合并。更简单的GRU模型越来越受欢迎。数学上GRU可以用表示如下公式：

GRU

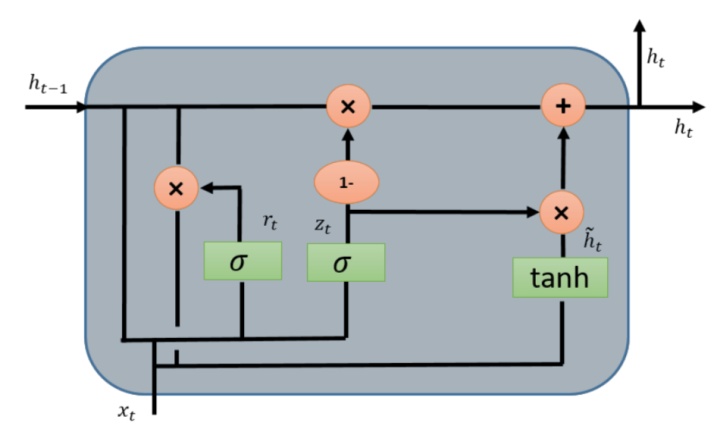
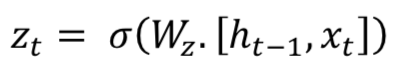
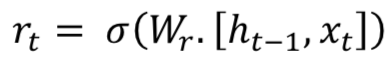
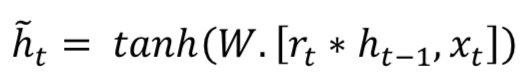
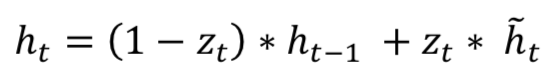
GRU需要较少的网络参数，这使模型更快。另一方面，如果有足够的数据和计算能力，LSTM可以提供更好的性能。

参考文献

https://skymind.ai/wiki/lstm
http://colah.github.io/posts/2015-08-Understanding-LSTMs/
http://karpathy.github.io/2015/05/21/rnn-effectiveness/
M Z Alom et al，“The History Began from AlexNet: A Comprehensive Survey on Deep Learning Approaches”，arXiv 1803.01164，2018