《机械传动》2019年  第43卷   第8期

文章编号：1004-2539(2019)08-0130-05

DOI：10.16578/j.issn.1004.2539.2019.08.024

引用格式：柴慧理, 叶美桃. 改进局部均值分解的齿轮箱复合故障特征提取[J]. 机械传动, 2019，43(8):130-134.

CHAI Huili， YE Meitao.Compound fault feature extraction of gearbox with improved local mean decomposition[J].Journal of Mechanical Transmission, 2019，43(8):130-134.

改进局部均值分解的齿轮箱复合故障特征提取

柴慧理 叶美桃

(山西交通职业技术学院车辆工程系，山西太原 030031)

摘要 在强噪声环境下，针对局部均值分解(Local Mean Decomposition，LMD)出现的模态混叠现象，提出了总体局部均值分解方法(Ensemble Local Mean Decomposition，ELMD)，但ELMD 中所添加的白噪声不能完全被中和，这会导致PF 分量受到所加白噪声的影响，导致重构误差增大。因此，提出基于PE-CELMD(Permutation Entropy-Complementary Ensemble Local Mean Decomposition)的齿轮箱复合故障诊断方法，该思路是在ELMD 的基础上通过添加成对白噪声再结合排列熵(Permutation Entropy，PE)的方法优化LMD。将该方法应用于仿真信号和实测信号，并通过与LMD、CELMD 对比，结果表明，PE-CELMD方法是一种有效的复合故障特征提取方法。

关键词 局部均值分解 排列熵 复合故障

0 引言

局部均值分解(Local Mean Decomposition，LMD)是由Jonathan S.Smith[1]提出的一种新的非线性非平稳信号的自适应处理方法，LMD 可以将非平稳的多分量信号自适应地分解为若干个乘积函数(Product Functions，PFs)分量，每个PF 分量的瞬时频率都具有物理意义，PF 分量实际上是一个单分量的调幅-调频信号，所以，LMD 的本质就是将一个多分量的信号自适应地分解为多个单分量的调幅-调频信号，这样使得LMD 适合处理非平稳、非线性的信号。程军圣等[2]通过对比LMD 与EMD(Empirical Mode Decomposition)，说明了LMD 能够在一定程度上抑制端点效应并具有虚假分量少、迭代次数少等优点。Wang 等[3]结合局部均值分解和能量色散率(EDR)用于齿轮箱的故障诊断；Liu等[4]集合LMD和PE提出了基于局部均值分解和多尺度熵的轴承故障诊断方法；Song R 等[5]结合局部均值分解和核主成分分析并将其应用于光纤陀螺振动误差分析。

针对LMD 出现模态混叠的问题，程军圣等提出了基于噪声辅助分析的总体局部均值分解方法[6]，它将有限幅值的白噪声加入原始信号中，再对加入了白噪声的信号进行LMD 分解，多次重复上述过程，每次添加不同的白噪声到原始信号中，最后将分解出的所有PF分量求均值，得到最终的分解结果。

文章提出基于PE-CELMD 的齿轮箱复合故障特征提取方法。考虑到排列熵(Permutation Entropy，PE)能够有效放大时间序列的微弱变化，在信号突变检测方面有着重要的应用价值；熵值可以反映时间序列的不确定程度，时间序列随机性越小，得到的熵值越小，时间序列随机性越大，得到的熵值越大[7]。因此，可以通过计算排列熵去掉异常信号;通过添加符号相反的白噪声可以完全中和所添加白噪声对LMD的影响，同时补充了ELMD的缺陷。

1 基本理论

1.1 排列熵

排列熵是一种用来衡量一维时间序列复杂程度的平均熵函数，该函数对信号的变换有很强的敏感性，可以将系统的微变信号放大，通过该方法可以检测出复杂系统的动力学突变，对于非线性、非平稳信号也有较好的检测效果。排列熵的基本算法为：

对一个长度为N 的时间序列{x(i)，i=1，2，…，n}进行相空间重构，可以得到一个时间序列，即

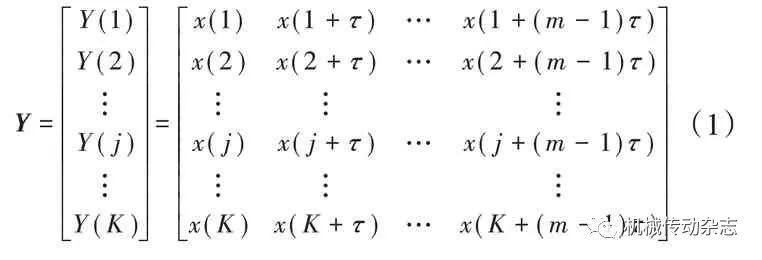
式中，j=1，2，3，…，K；K +(m-1)τ= n；m 为嵌入维数；τ为延迟时间。

如果在重构分量中有着相等的值，即

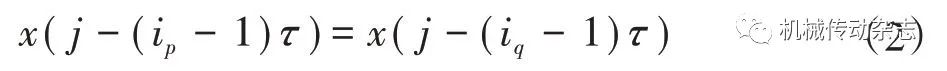
则按照ip 和iq 的大小排序，即如果ip ＜iq，x( j-(ip-1)τ)≤x( j-(iq-1)τ)。因此，对于重构矩阵Y的任何重构分量Y(j)都能得到一组序列，即

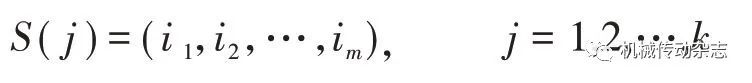
设每种位置索引序列出现的概率为客户p1、p2、…、pk，计算出p1、p2、…、pk的值，根据熵的形式将时间序列{x(i),i=1,2,…,n}的k 种不同索引序列的排列熵定义为

将Hp进行归一化处理，可以使排列熵的比较更加方便，常用lnm!进行归一化处理，即

其中，0 ≤Hp ≤1，Hp 的大小反映了时间序列{x(i),i=1,2,…,n}的随机程度。若时间序列越规则，则Hp的值越小；反之，时间序列越随机，则Hp的值越大；Hp的变化放大了时间序列的微小变化。

1.2 PE-CELMD齿轮箱复合故障诊断方法

PE-CELMD方法如下：

(1)在原始信号x(t)中，分别添加成对的、符号相反的、均值为0 的白噪声信号ni(t)和-ni(t)，得到即

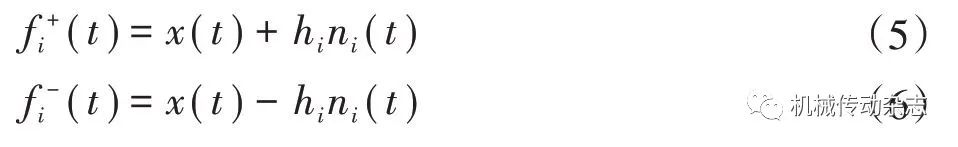
其中，hi 代表白噪声的幅值，其作用是改变原信号极值点的分布，i=1，2，…，M，M 为添加的白噪声对数。

(2)分别对进行LMD 分解，得到第1层PF分量

(3)集成平均上述分量，有

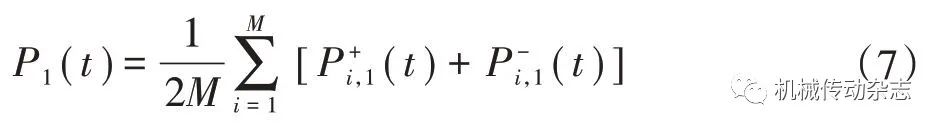
(4)计算出P1(t)的熵值，并判断该分量是否为高噪声分量：若熵值θ1 ＞θ0，则认为是高噪声分量。

(5)若I1(t)是高噪声分量，按照步骤(2)～(4)，计算出P1(t)、P2(t)……直至出现θm ≤θ0。

(6)将高噪声信号P1(t)、P2(t)、…、Pm-1(t)从原始信号中分离，低噪声信号组成新的重构信号，即

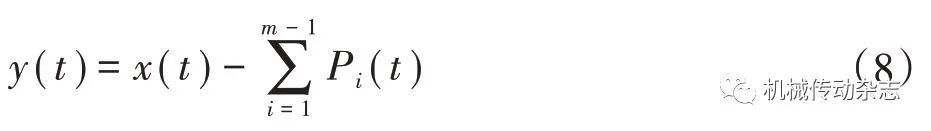
(7)用LMD分解重构信号y(t)得到PF分量。

(8)通过CELMD 和排列熵去除高噪声分量之后，信号中依然会存在少量噪声及由于辅助噪声引起的误差，所以，用SG 滤波对低噪声分量进行平滑处理，得到最终的分解结果。

(9)得出每个PF 分量的频谱图，进行故障特征提取。

2 仿真分析

为了验证提出的PE-CELMD 复合故障提取方法的有效性，给出的仿真信号如式(9)所示，对应的时域波形如图1(a)，它们的合成仿真信号如图1(b)所示。

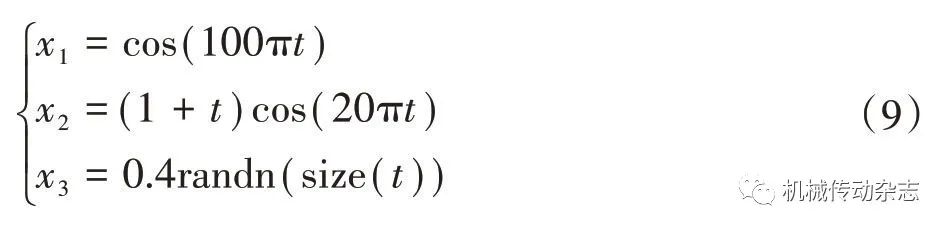
对该合成信号添加30 对均值为0 的白噪声信号，得到对其进行LMD 分解，第1 层的PF 分量平均得到P1(t)，结果如图2 中P1所示，计算出第1 层PF 分量的排列熵θ1 为0.902 9，因为θ1 ＞θ0，所以，第1 层为异常信号；第2 层的PF 分量平均得到P2(t)，结果如图2 中P2所示，计算排列熵θ1 为0.719 6，因为θ2 ＞θ0，所以，第2 层也为异常信号；第3 层如图2 中P3所示，计算出排列熵θ1 为0.343 8，因为θ1 小于0.6，所以，第3 层为正常信号，分解停止。

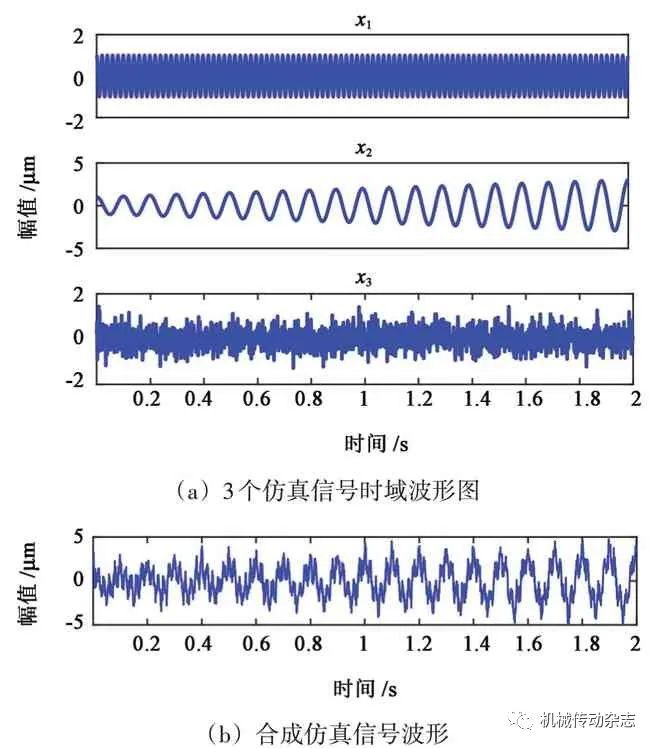
图1 仿真信号的时域波形图

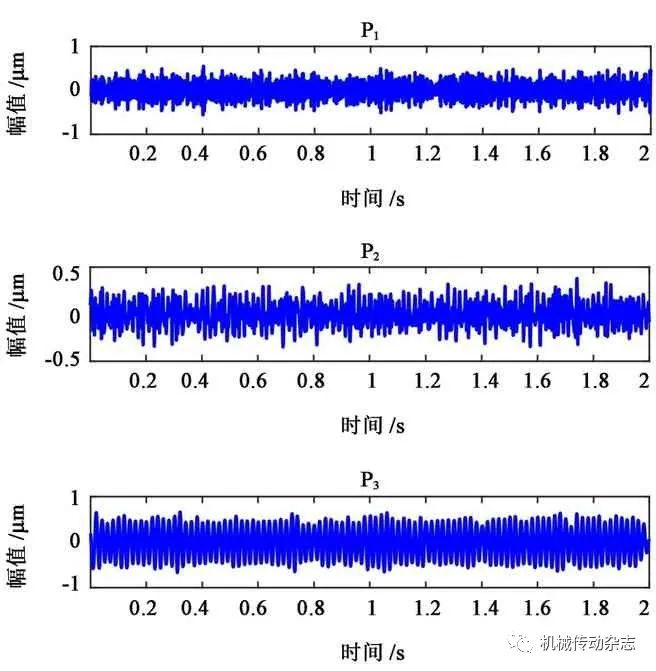
图2 CELMD分解的前三层模态函数

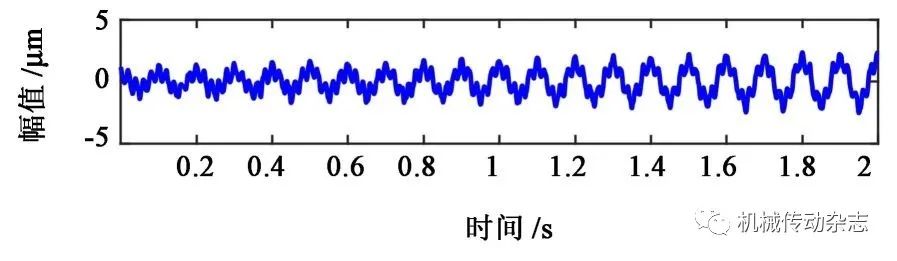
图3 去除异常信号后的信号的时域波形图

将PF1、PF2高频噪声从原信号中去除。重构剩余信号的时域波形如图3 所示。对图3 进行LMD 分解，再对各分量进行SG 滤波便得到最终的分解结果，如图4所示。除了余量外的剩余两层为原仿真信号的两个分量，没有模态混叠现象，降噪效果较好。

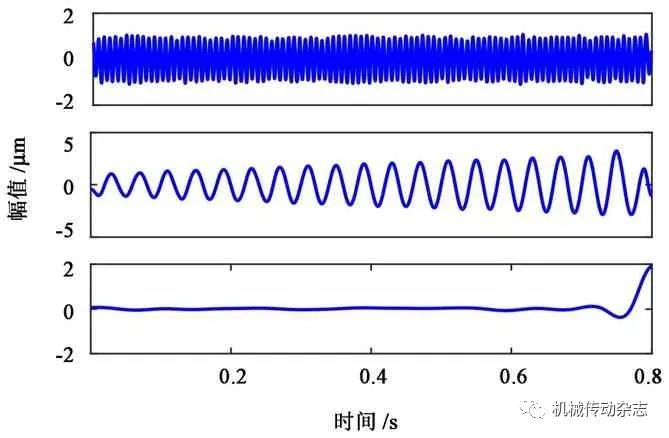
图4 仿真信号PE-CELMD

同时，选用LMD、CELMD 与所提出方法进行对比，分解结果如图5(a)、图5(b)所示。通过LMD 分解出的PF 分量中，第1、2 层为噪声，在第4 层和第5 层出现了同一模态，存在明显的模态混叠，第6、7、8 层为伪分量，并分解出了较多的虚假分量；CELMD 通过添加辅助白噪声，在一定程度上抑制了模态混叠，依然存在伪分量且计算量较大。

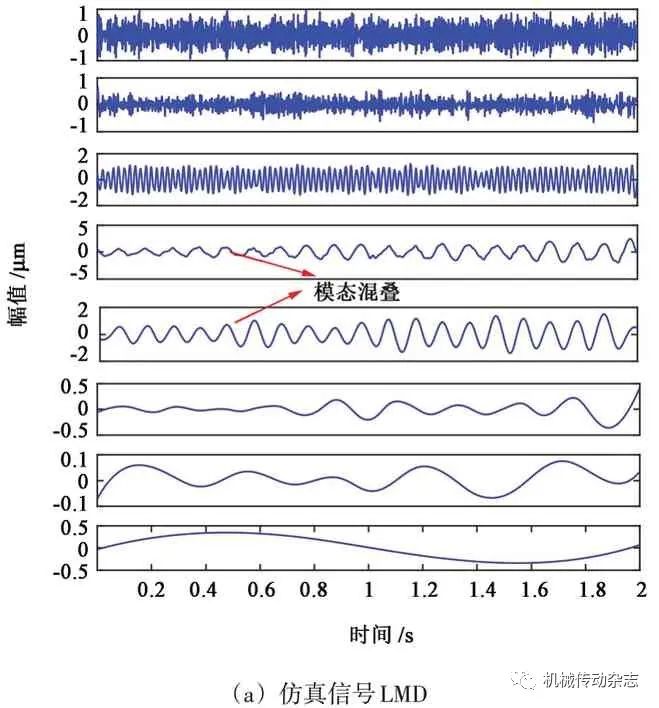
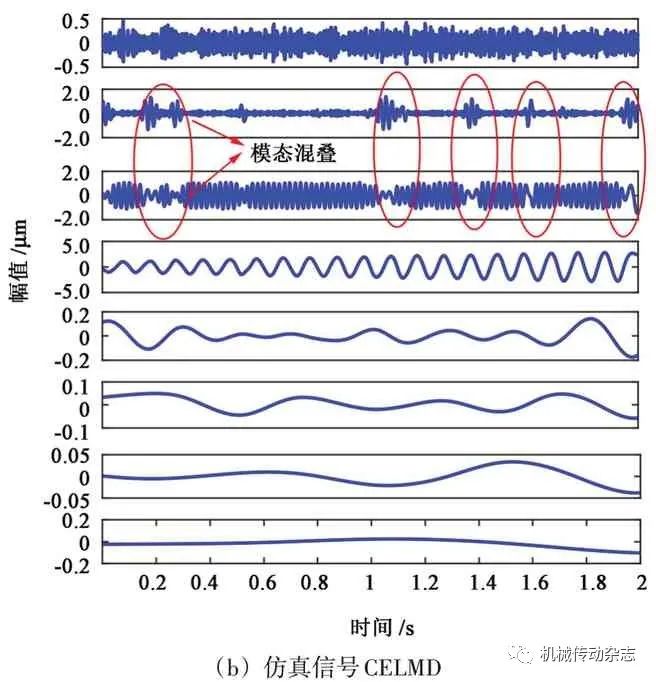
图5 对原信号用LMD、CELMD分解

3 试验分析

试验台的试验装置主要有试验轴承、转速显示器、电机、试验齿轮、转轴、三向加速度传感器等。试验轴承型号为32212，三向加速度传感器型号为YD77SA(灵敏度为0.01 V/ms2)。滚动体故障频率为72 Hz，轴承外圈的故障频率160 Hz，齿轮的啮合频率为360 Hz，采样点数为2 048个，采样频率8 000 Hz。复合故障包括齿轮剥落、轴承外圈缺陷、滚动体缺陷。试验台如图6所示，轴承故障如图7所示。

图6 齿轮传动试验台

1.调速电机；2.联轴器；3.陪试齿轮箱；4.转速转矩仪；5.扭力杆；6.试验齿轮箱；7.三向加速度传感器1#；8.三向加速度传感器2#

图7 电火花加工故障轴承

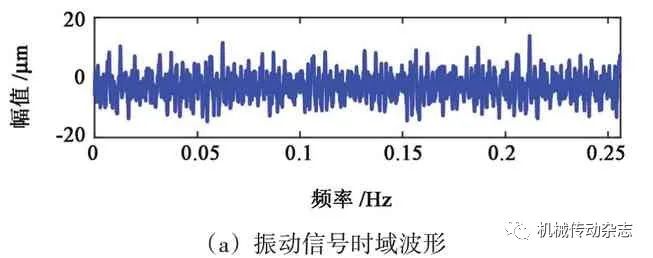
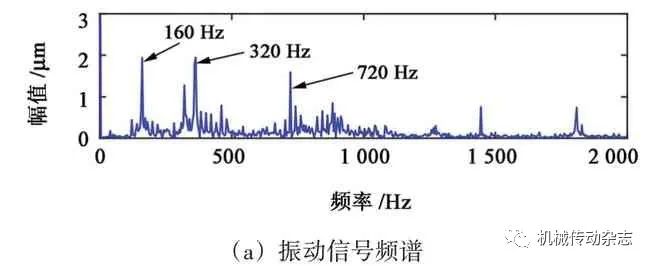
图8 实测信号的时域和频谱分析结果

振动信号的时域波形及其频谱如图8 所示，160 Hz、360 Hz、720 Hz 分别为轴承外圈、齿轮的啮合频率及倍频；滚动体振动信息由于噪声的存在，在频谱中并不突出，因此，需要对原振动信号进行自适应分解。进一步对原信号进行PE-CELMD 分析，结果如图9 所示，该方法将原振动信号分解为5层，除了余量，其他4 层均具有物理意义，其中，720 Hz、360 Hz、160 Hz、72 Hz 分别存在不同的PFs中。该方法不仅克服了模态混叠现象，也将原信号的3个故障特征依次分离，进一步说明该方法在很大程度上抑制了模态混叠现象且未出现伪分量。

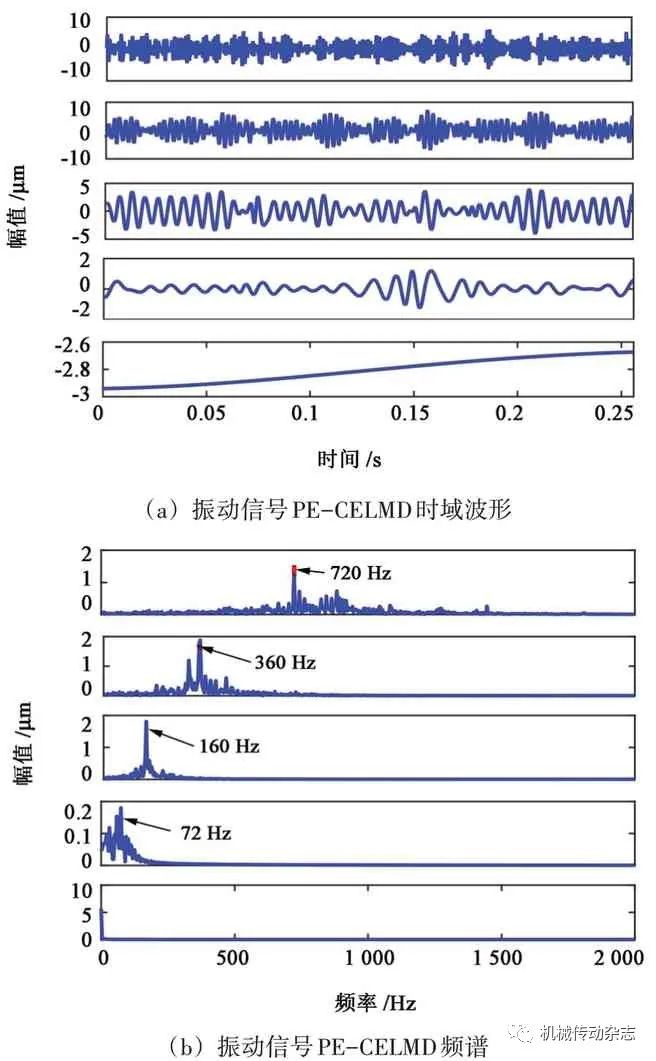
图9 PE-CELMD分解结果

将CELMD与文中所提方法对比，结果如图10所示。通过频域可知，前两层为高频分量，且存在模态混叠现象，只有第3、4、5 层为有效分量，因此，CELMD易出现误诊断现象。

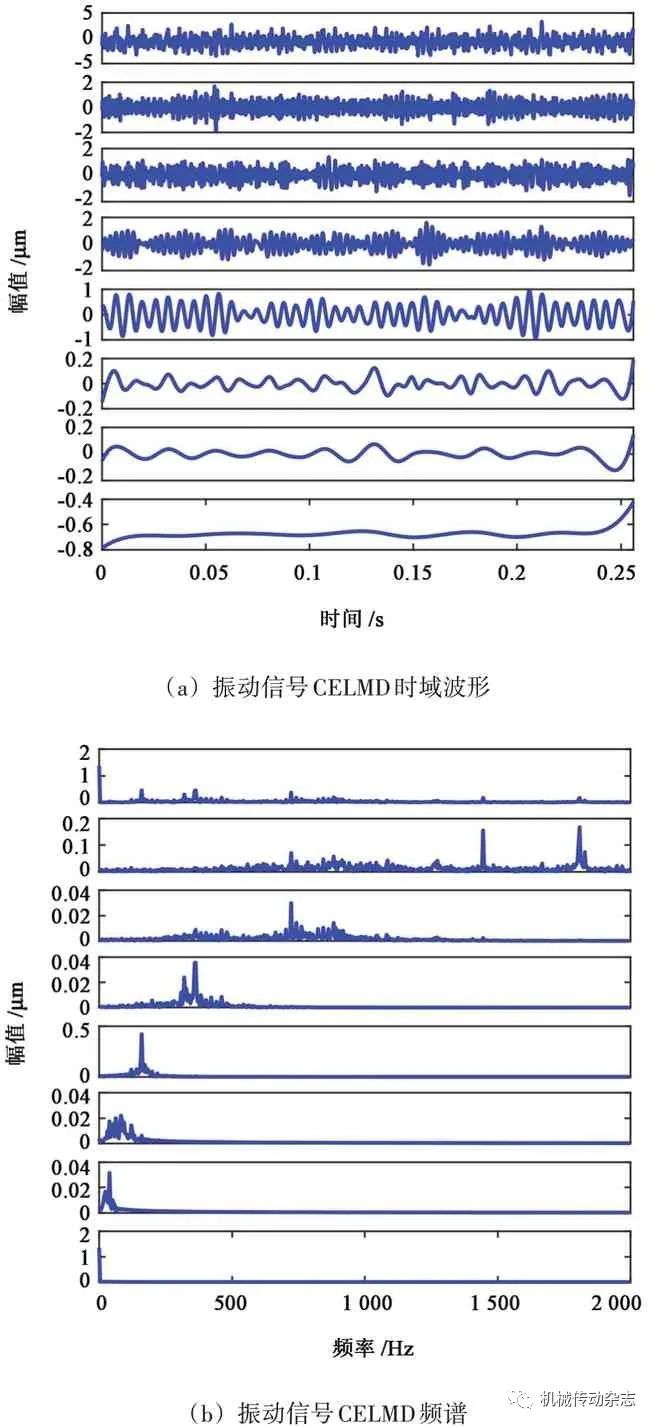
图10 CELMD分解结果

4 结论

(1)LMD 分解在受到噪声干扰时会出现模态混叠现象。提出的基于PECELMD 的齿轮箱复合故障特征提取方法，通过结合CELMD 和PE 可以将高频白噪声分量直接剔除。

(2)通过与LMD、CELMD 等方法对比，进一步证明了该方法的可行性，此方法为复合故障特征提取提供了一条新思路，具有一定的工程应用价值。

参考文献

［1］JONATHAN S S.The local mean decomposition and its application to EEG perception data［J］.Journal of the Royal Society Interface，2005，2(5)：443-454.

［2］程军圣，杨宇，于德介.局部均值分解方法及其在齿轮故障诊断中的应用［J］.振动工程学报，2009，22(1)：76-84.

［3］WANG Y，HE Z，ZI Y.A decomposition method based on improved local mean decomposition and its application in rub-impact fault diagnosis［J］.Measurement Science&Technology，2009，20(2)：28.

［4］LIU H，HAN M.A fault diagnosis method based on local mean decomposition and multi-scale entropy for roller bearings［J］.Mechanism&Machine Theory，2014，75(5)：67-78.

［5］SONG R，CHEN X.Analysis of fiber optic gyroscope vibration error based on improved local mean decomposition and kernel principal component analysis［J］.Applied Optics，2017，56(8)：2265.

［6］程军圣，张亢，杨宇.基于噪声辅助分析的总体局部均值分解方法［J］.机械工程学报，2011，47(3)：55-62.

［7］BANDT C，POMPE B.Permutation entropy：a natural complexity measure for time series［J］.Physical Review Letters，2002，88(17)：174102.

Compound Fault Feature Extraction of Gearbox with Improved Local Mean Decomposition

Chai Huili Ye Meitao
(Department of Vehicle Engineering，Shanxi Traffic Vocational And Technical College，Taiyuan 030031，China)

Abstract In the case of strong noise, Ensemble local mean decomposition (ELMD) is proposed for the modal aliasing phenomenon of local mean decomposition(LMD).However,the white noise added in ELMD cannot be completely neutralized,which will result in the reconstruction error increases due to the Product functions(PF)components to be affected by the added white noise.Therefore,a compound fault feature extraction method for gearbox based on PE-CELMD(Permutation Entropy-Complementary Ensemble local mean decomposition) is proposed.The idea is to optimize ELMD by adding pairwise white noise in combination with Permutation Entropy (PE) method based on ELMD.The method is applied to the simulated signal and the measured signal, and compared with LMD and CELMD, the results show that the PE-CELMD method is an effective compound fault feature extraction method.

Key words Local mean decomposition Permutation entropy Compound fault

收稿日期：2018-10-16

修回日期：2018-11-06

基金项目：国家自然科学基金(59975064)

山西省基础研究项目(2015011063)

作者简介：柴慧理(1970—)，男，山西太原人，硕士，副教授，主要研究方向为汽车机电。

专家点评：

复合故障诊断是故障诊断技术的一个难点,也是未来故障诊断研究领域的重点之一。

文章通过添加成对白噪声再结合排列熵的方法对ELMD方法进行优化，一定程度上降低了所加白噪声对PF的影响。一方面是对现有成熟算法的合理利用和嫁接，同时也体现了文章作者对所采用算法及对比算法的理解。

文章的创新点大致有二：LMD是将振动信号分解为若干由不同尺度的包络信号和纯调频信号乘积得到的PF分量；ELMD是对LMD的一种改进，利用白噪声来解决模态混叠问题，是因为白噪声具有频率分布均匀的统计特性。这篇文章提出的方法与LMD的区别之一就在于对加入到振动信号中，以便形成混合信号的白噪声进行设计；另一点在于作者利用了排列熵对时序信号变化的有效放大这一点。

文章研究思路清晰，结构完整，理论、仿真和试验部分均有较为详细的描述。逻辑较为严谨，在仿真部分将改进的算法与其他算法的处理结果进行对比。

END

查看更多内容，请点击