一、实验目的
通过MATLAB仿真验证抽样定理，进一步加深对抽样定理的理解。
二、实验原理
1. 连续信号的采样
对某一连续时间信号f(t)的采样原理图为：
由图可知，
，其中，单位冲激采样信号
的表达式为：
其傅里叶变换为
，其中
,设
为
的傅里叶变换，
的频谱为
，根据傅里叶变换的频域卷积定理：
若设
是带限信号，带宽为
，即当
时，
的频谱
，则
经过采样后的频谱
就是
在频率轴上搬移至
处(幅度为原频谱的
倍)。因此，当
时，频谱不发生混叠；当
时，频谱发生混叠。
2.连续信号的恢复
设信号
被采样后形成的采样信号为
，信号的重构是指由
经内插处理后，恢复出原来的信号
的过程，因此又称为信号恢复。设
为带限信号，带宽为
，经采样后的频谱为
。设采样频谱
，则
是以
为周期的谱线。现取一个频率特性为
的理想低通滤波器与
相乘，得到的频谱即为原信号的频谱
。根据时域卷积定理：
其中，
因此
,信号的采样频率为ωs，信号的采样周期为Ts,信号的最高频率为ωm,低通截止频率为ωc
(1)当ωs=2ωm ,ωc=ωm时，用matlab对信号进行采样及恢复，分析误差，画出波形；
(2)当ωs=4ωm ,ωc=2ωm时，用matlab对信号进行采样及恢复，分析误差，画出波形；
(3)当ωs=ωm ,ωc=ωm时，用matlab对信号进行采样及恢复，分析误差，画出波形；
分析：
的傅里叶变换为：
,
信号的最高频率为ωm=1，根据采样定理，当采样频率ωs=2ωm时为临界采样，当ωs>2ωm过采样，ωs<2ωm欠采样；恢复时，低通滤波器的的截止频率(ωs-ωm)≥ωc≥ωm
matlab里利用sinc函数实现Sa(t)，即Sa(t)=sinc(t/pi)
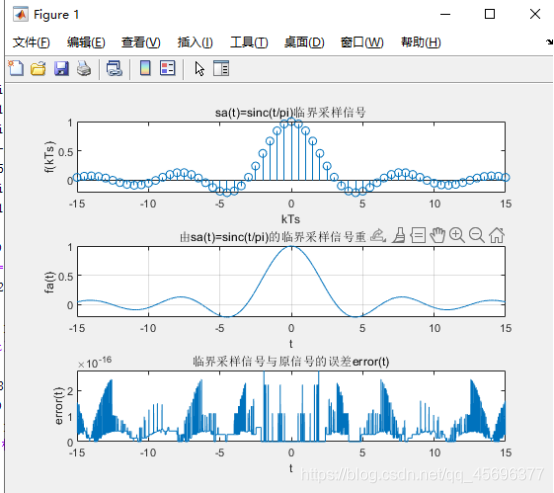
(1)在临界采样状态下实现对信号Sa(t)的采样及由该采样信号恢复Sa(t)的参考程序如下：
clear all;
wm=1; ％信号带宽
wc=wm; ％滤波器截止频率
Ts=pi/wm; ％采样间隔
ws=2*pi/Ts; ％采样角频率
n=-100:100; ％时域采样点数
nTs=n*Ts; ％时域采样点
f=sinc(nTs/pi); ％信号f(nTs)的表达式
t=-15:0.005:15;
fa=f*Ts*wc/pi*sinc((wc/pi)*(ones(length(nTs),1)*t-nTs'*ones(1,length(t)))); ％信号重构
error=abs(fa-sinc(t/pi)); ％求重构信号与原信号的误差
t1=-15:0.5:15;
f1=sinc(t1/pi);
subplot(3,1,1);
stem(t1,f1);
xlabel('kTs'); ylabel('f(kTs)');
title('sa(t)=sinc(t/pi)临界采样信号');
subplot(3,1,2);
plot(t,fa);
xlabel('t'); ylabel('fa(t)');
title('由sa(t)=sinc(t/pi)的临界采样信号重构sa(t)');
grid on;
subplot(3,1,3);
plot(t,error);
xlabel('t'); ylabel('error(t)');
title('临界采样信号与原信号的误差error(t)');
运行结果如下：
三、实验内容
1、实现例子中的第(2)(3)问；
(2)程序如下：
clear all;
wm=1; %信号带宽
wc=2*wm; %滤波器截止频率
Ts=pi/wm; %采样间隔
ws=2*2*pi/Ts; %采样角频率
n=-100:100; %时域采样点数
nTs=n*Ts; %时域采样点
f=sinc(nTs/pi); %信号f(nTs)的表达式
t=-15:0.005:15;
fa=f*Ts*wc/pi*sinc((wc/pi)*(ones(length(nTs),1)*t-nTs'*ones(1,length(t)))); %信号重构
error=abs(fa-sinc(t/pi)); %求重构信号与原信号的误差
t1=-15:0.5:15;
f1=sinc(t1/pi);
subplot(3,1,1);
stem(t1,f1);
xlabel('kTs'); ylabel('f(kTs)');
title('sa(t)=sinc(t/pi)临界采样信号');
subplot(3,1,2);
plot(t,fa);
xlabel('t'); ylabel('fa(t)');
title('由sa(t)=sinc(t/pi)的临界采样信号重构sa(t)');
grid on;
subplot(3,1,3);
plot(t,error);
xlabel('t'); ylabel('error(t)');
title('临界采样信号与原信号的误差error(t)');
运行结果如下：
(3)程序如下：
clear all;
wm=1; %信号带宽
wc=wm; %滤波器截止频率
Ts=pi/wm; %采样间隔
ws=pi/Ts; %采样角频率
n=-100:100; %时域采样点数
nTs=n*Ts; %时域采样点
f=sinc(nTs/pi); %信号f(nTs)的表达式
t=-15:0.005:15;
fa=f*Ts*wc/pi*sinc((wc/pi)*(ones(length(nTs),1)*t-nTs'*ones(1,length(t)))); %信号重构
error=abs(fa-sinc(t/pi)); %求重构信号与原信号的误差
t1=-15:0.5:15;
f1=sinc(t1/pi);
subplot(3,1,1);
stem(t1,f1);
xlabel('kTs'); ylabel('f(kTs)');
title('sa(t)=sinc(t/pi)临界采样信号');
subplot(3,1,2);
plot(t,fa);
xlabel('t'); ylabel('fa(t)');
title('由sa(t)=sinc(t/pi)的临界采样信号重构sa(t)');
grid on;
subplot(3,1,3);
plot(t,error);
xlabel('t'); ylabel('error(t)');
title('临界采样信号与原信号的误差error(t)');
运行结果如下：
2、当信号f(t)=ε(t+1)-ε(t-1),用matlab实现信号的采样和重建,并分析误差
(1)ωm=2π，ωc=1.2ωm,Ts=0.25
(2)ωm=2π，ωc=1.2ωm,Ts=1
(求大佬指点)
四、实验报告要求
1、 简述实验目的及实验原理
(1).加深理解采样对信号的时域和频域特性的影响;
(2).加深对 采样定理的理解和掌握，以及对信号恢复的必要性;
(3).掌握对连续信号在时域的采样与重构的方法。
2、 写出程序清单
3、 记录实验结果，并进行原理阐述
1.加深理解采样对信号的时域和频域特性的影响;
2.加深对 采样定理的理解和掌握，以及对信号恢复的必要性;
3.掌 握对连续信号在时域的采样与重构的方法。
4、 收获与建议
收获：通过这次实验，加深了对于采样定理的理解，对于信号与系统这么抽象的课程有了更加直观的了解。
建议：有的实验版上的可调电阻引脚断开了，希望修复。
