史上最容易理解的暴力递归和动态规划~~
介绍递归和动态规划
1, 把问题转化为规模缩小了的同类问题的子问题
2, 有明确的不需要继续进行递归的条件(base case)
3, 有当得到了子问题的结果之后的决策过程
4, 不记录每一个子问题的解(区别于动态规划2)
1, 从暴力递归中来
2, 将每一个子问题的解记录下来, 避免重复计算
3, 把暴力递归的过程, 抽象成了状态表达
4, 并且存在化简状态表达, 使其更加简洁的可能
动态规划其实是由暴力递归演变而来的,每个动态规划的接法基本都能找到其动态规划的版本~
他们的关系如下:
暴力递归------》依赖关系(套路,即记忆关系)------》动态规划
下面以一道题为例子来向大家详细的介绍一下:
先理解一下题意:
给定一个数组和一个整数,可以随便选择arr数组里面的数字,看看累加起来能不能得到aim,可以得到就返回true,不可以返回false
eg :arr[] = { 3, 2, 9, 7 }; Aim = 21;返回true 3+2+9+7=21
arr[] = { 3, 2, 9, 7 }; Aim = 13;返回false,无法组合得到13
思路分析:
先用暴力递归的方式来解决:
先看一下方法的参数,参数有arr[]和Aim是题目提供的,我们自己定义的有i和sum,这两个参数是什么意思呢?
他们的含义是,在一个数组中,从i下标开始,可以任意去i后面的数进行累加,累加的和为sum,看图:
如果你能想到这个图或者说看到这个图,你就已经成功了一半~~
可以发现,要判断这个数组中是否有满足要求的组合,只要看最后一行是否有相应的aim值就可以了。
所以,就有了下面的暴力递归:
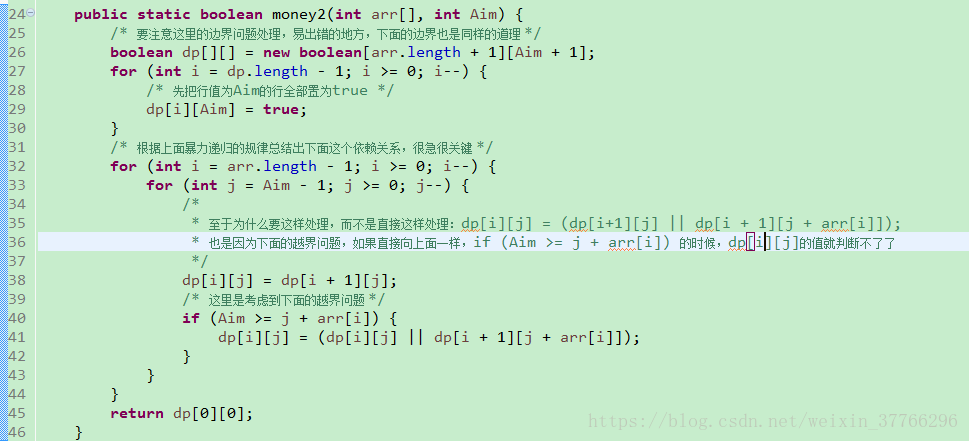
暴力递归之后,就是动态规划了~
来来来,重点来了,从暴力递归转变到动态规划,跟题意是没有半毛钱关系的~
下面划重点了:
暴力递归------》依赖关系(套路,即记忆关系)------》动态规划
这里还差了个依赖关系:
啥都别说了,先画个图吧嘻嘻~
还是以上面那个例子为主:
arr[3] = {2,3,7};
aim = 10;
那么i的取值范围就是0~3了
sum的取值则是2+3+7=12即(0~12)
先看暴力破解法的basecase:
辣么,第三行sum等于Aim的值就为true,其他为false;
再看基本关系:
通过细细分析,可以得到下面的依赖关系图了~
图中的方框加×是(i,sum)的依赖,也就是说,要想得到(I,sum)的值,只要知道两个方框加×里面的值就可以推出来了( 不是我说的,是程序里面体现出来的)那么,因为第三列的值都知道了,那么其他列的值肯定也可以通过这一列的值推出来,那么我们所要求的(0,0)的值不就出来了吗?
这个依赖关系出来之后,那么动态规划的解也就出来了~~~(开心)
其实这个方法我也是思考了很久才领悟的~
希望对你们也能有所帮助~~不懂欢迎留言,懂得帮忙点个赞~~~











 toString三者之间的区别~)







)






